Como discutimos en el Conjunto 1 , las siguientes son las dos propiedades principales de un problema que sugieren que el problema dado se puede resolver usando programación dinámica:
1) Subproblemas superpuestos
2) Subestructura óptima
Ya hemos discutido la propiedad del subproblema superpuesto en el Conjunto 1 . Analicemos aquí la propiedad de la subestructura óptima.
2) Subestructura óptima: un problema dado tiene propiedad de subestructura óptima si la solución óptima del problema dado se puede obtener mediante el uso de soluciones óptimas de sus subproblemas.
Por ejemplo, el problema de la ruta más corta tiene la siguiente propiedad de subestructura óptima:
si un Node x se encuentra en la ruta más corta desde un Node de origen u hasta el Node de destino v, entonces la ruta más corta de u a v es una combinación de la ruta más corta de u a x y la ruta más corta de x a v. El algoritmo estándar de ruta más corta de todos los pares como Floyd-Warshall y el algoritmo de ruta más corta de fuente única para bordes de peso negativo como Bellman-Ford son ejemplos típicos de programación dinámica.
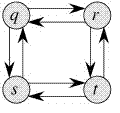
Por otro lado, el problema de la ruta más larga no tiene la propiedad de subestructura óptima. Aquí, por Camino más largo, nos referimos al camino simple más largo (camino sin ciclo) entre dos Nodes. Considere el siguiente gráfico no ponderado dado en el libro CLRS . Hay dos caminos más largos de q a t: q→r→t y q→s→t. A diferencia de los caminos más cortos, estos caminos más largos no tienen la propiedad de subestructura óptima. Por ejemplo, el camino más largo q→r→t no es una combinación del camino más largo de q a r y el camino más largo de r a t, porque el camino más largo de q a r es q→s→t→r y el El camino más largo de r a t es r→q→s→t.
Cubriremos algunos problemas de ejemplo en publicaciones futuras sobre programación dinámica .
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Referencias:
http://en.wikipedia.org/wiki/Optimal_substructure
Libro CLRS
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA