El determinante de una array es una propiedad escalar de esa array . El determinante es un número especial que se define solo para arrays cuadradas (plural de array). La array cuadrada tiene el mismo número de filas y columnas.
El determinante se usa para saber si la array se puede invertir o no, es útil en el análisis y solución de ecuaciones lineales simultáneas (regla de Cramer), se usa en cálculo, se usa para encontrar el área de triángulos (si se dan las coordenadas) y más. El determinante de una array A se denota por |A| o det(A) .
Propiedades de los Determinantes de Arrays:
- El determinante evaluado en cualquier fila o columna es el mismo.
- Si todos los elementos de una fila (o columna) son ceros, entonces el valor del determinante es cero.
- El determinante de una array Identidad (
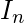 ) es 1 .
) es 1 . - Si se intercambian filas y columnas, el valor del determinante permanece igual (el valor no cambia). Por lo tanto, det(A) = det(
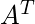 ) , aquí
) , aquí 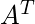 está la transpuesta de la array A.
está la transpuesta de la array A. - Si se intercambian dos filas (o dos columnas) de un determinante, el valor del determinante se multiplica por -1 .
- Si todos los elementos de una fila (o columna) de un determinante se multiplican por algún número escalar k, el valor del nuevo determinante es k veces el determinante dado. Por lo tanto, si A es una array cuadrada de n filas y K es un escalar cualquiera. Entonces |KA| =
 |A| .
|A| . - Si dos filas (o columnas) de un determinante son idénticas, el valor del determinante es cero.
- Sean A y B dos arrays, entonces det(AB) = det(A)*det(B) .
- Si A es una array entonces, |
 | =
| =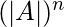 .
. - El determinante de la inversa de la array se puede definir como |
 | =
| = .
. - Determinante de array diagonal, array triangular (array triangular superior o array triangular inferior) es producto de elemento de la diagonal principal.
- En un determinante, cada elemento en cualquier fila (o columna) consta de la suma de dos términos, entonces el determinante se puede expresar como la suma de dos determinantes del mismo orden. Por ejemplo,

- Si B se obtiene sumando c veces un renglón de A a un renglón diferente, el
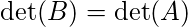 .
. - Sea A una array entonces,
|adj(A)| =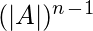
|adj(adj(A))| = ,
,
Aquí adj(A) es adjunto a la array A. - Si el valor del determinante
 se vuelve cero sustituyendo x =
se vuelve cero sustituyendo x = 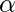 , entonces x-
, entonces x- 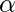 es un factor de
es un factor de  .
. - Aquí, cij denota el cofactor de elementos de aij en
 .
.


- En un determinante la suma del producto de los elementos de cualquier fila (o columna) con los cofactores de los elementos correspondientes de cualquier otra fila (o columna) es cero. Por ejemplo,
d = ai1*Aj1 + ai2*Aj2 + ai3*Aj3 +…… + ain*Ajn, aquí Aj1, Aj2, Aj3…Ajn son cofactores a lo largo de los elementos de la j-ésima fila. - Sean
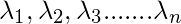 los valores propios de A (array cuadrada de orden n). Entonces det(A) =
los valores propios de A (array cuadrada de orden n). Entonces det(A) =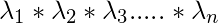 , producto de valores propios.
, producto de valores propios.