proto de Emde Boas Árboles | Conjunto 1 (Antecedentes e Introducción)

Consideremos el siguiente enunciado del problema y pensemos en diferentes soluciones para él.

Dado un conjunto S de elementos tales que los elementos se toman del universo {0, 1, …. u-1}, realice las siguientes operaciones de manera eficiente.

• insert(x) : Agrega un elemento x al conjunto+ S.
• isEmpty() : Devuelve verdadero si S está vacío, de lo contrario, es falso.
• find(x) : Devuelve verdadero si x está presente en S, de lo contrario, es falso.
• insert(x) : Inserta un elemento x en S.
• delete(x) : Elimina un elemento x de S.
• max() : Devuelve el valor máximo de S.
• min() : Devuelve el valor mínimo de S.
• sucesor(x) : Devuelve el valor más pequeño de S que es mayor que x.
• predecesor(x) : Devuelve el valor más grande en S que es más pequeño que x.

Soluciones diferentes
A continuación se presentan diferentes soluciones para el problema anterior.

• Una solución para resolver el problema anterior es utilizar un árbol de búsqueda binaria autoequilibrado como el árbol rojo-negro, el árbol AVL , etc. Con esta solución, podemos realizar todas las operaciones anteriores en tiempo O (Inicio de sesión).
• Otra solución es usar Binary Array (o Bitvector) . Creamos una array de tamaño u y marcamos la presencia y ausencia de un elemento como 1 o 0 respectivamente. Esta solución es compatible con insert(), delete() y find() en tiempo O(1), pero otras operaciones pueden tomar tiempo O(u) en el peor de los casos.
• El árbol Van Emde Boas (o árbol vEB) admite operaciones de inserción(), eliminación, búsqueda(), sucesor() y predecesor() en el tiempo O (Log Log u), y max() y min() en O (1) tiempo. Nota : en la solución BST, tenemos complejidad de tiempo en términos de n, aquí tenemos complejidad de tiempo en términos de u. Entonces, el árbol de Van Emde Boas puede no ser adecuado cuando u es mucho más grande que n.

Antecedentes (superposición de una estructura de árbol binario en una solución de array binaria)
Las complejidades de tiempo de max(), min(), sucesor() y predecesor() son altas en el caso de la solución de array binaria. La idea es reducir las complejidades temporales de estas operaciones superponiendo una estructura de árbol binario sobre ellas.

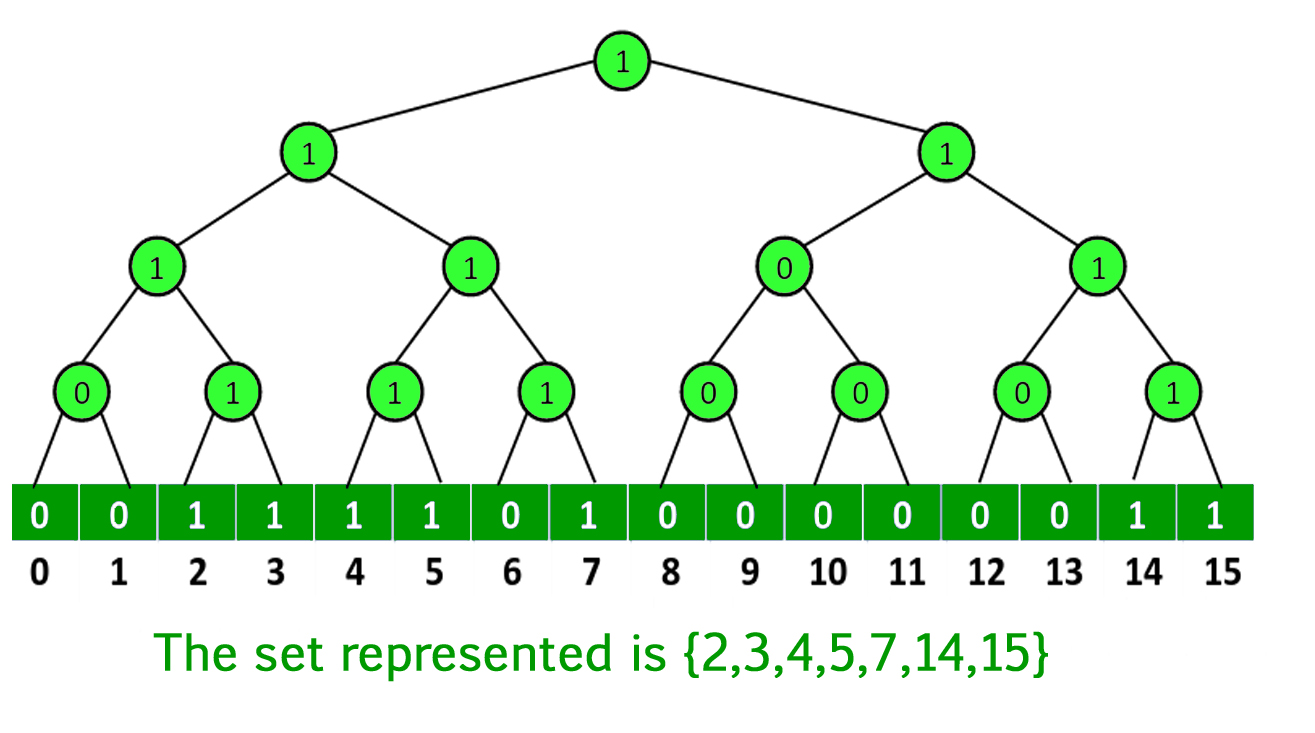
Explicación de la estructura anterior:

1. Las hojas del árbol binario representan las entradas de la array binaria.
2. Un Node interno tiene el valor 1 si alguno de sus hijos tiene el valor 1, es decir, el valor de un Node interno es O bit a bit de todos los valores de sus hijos.

Con la estructura anterior, hemos optimizado max(), min(), sucesor() y predecesor() para cronometrar la complejidad O(Log u).

1. min() : Comience con la raíz y avance hasta una hoja usando las siguientes reglas. Mientras atraviesa, elija siempre el hijo más a la izquierda, es decir, vea si el hijo izquierdo es 1, vaya al hijo izquierdo, de lo contrario, vaya al hijo derecho. El Node hoja al que llegamos de esta manera es mínimo. Dado que viajamos a través de la altura del árbol binario con hojas u, la complejidad del tiempo se reduce a O (Log u)
   
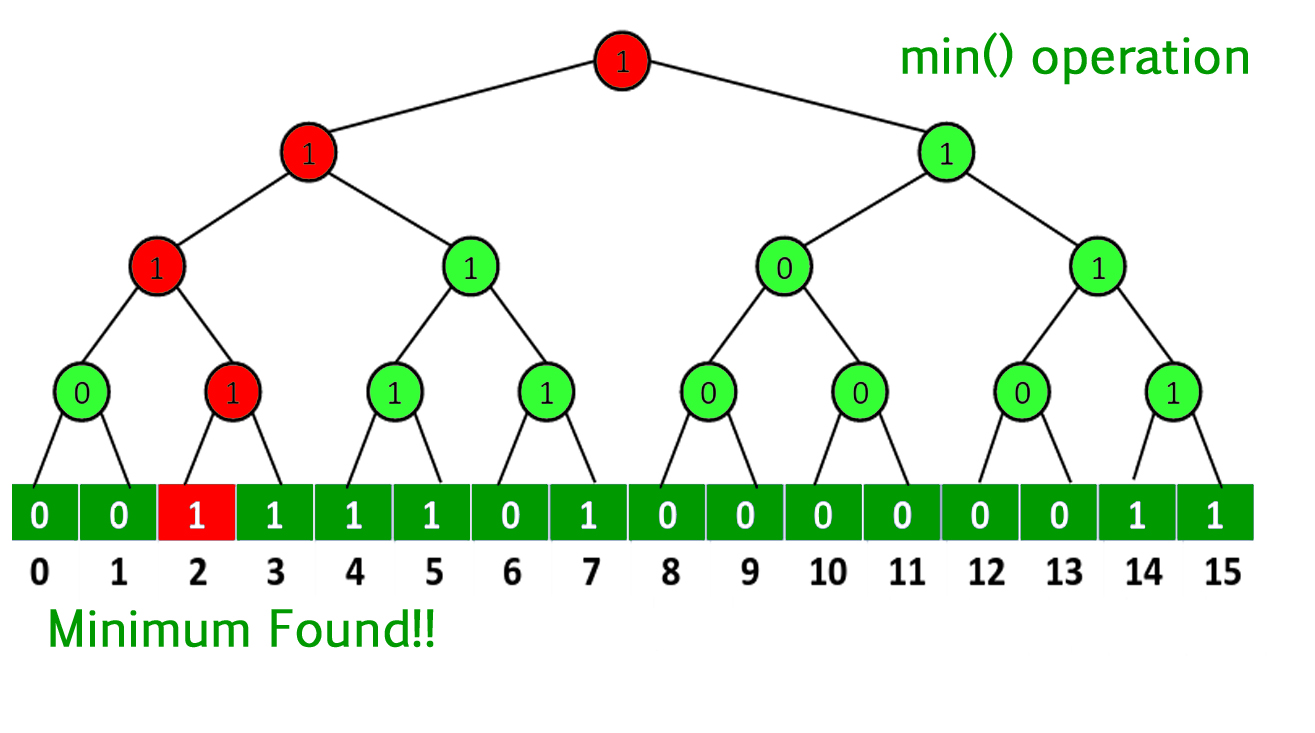
2. max() : Similar a min(). En lugar de niño izquierdo, preferimos niño apretado.
3. sucesor(x) : Comienza con el Node hoja indexado con x y viaja hacia la raíz hasta llegar a un Node z cuyo hijo derecho es 1 y no en el mismo camino recorrido hasta ahora. Deténgase en z y viaje hasta una hoja siguiendo el Node más a la izquierda con valor 1.
   
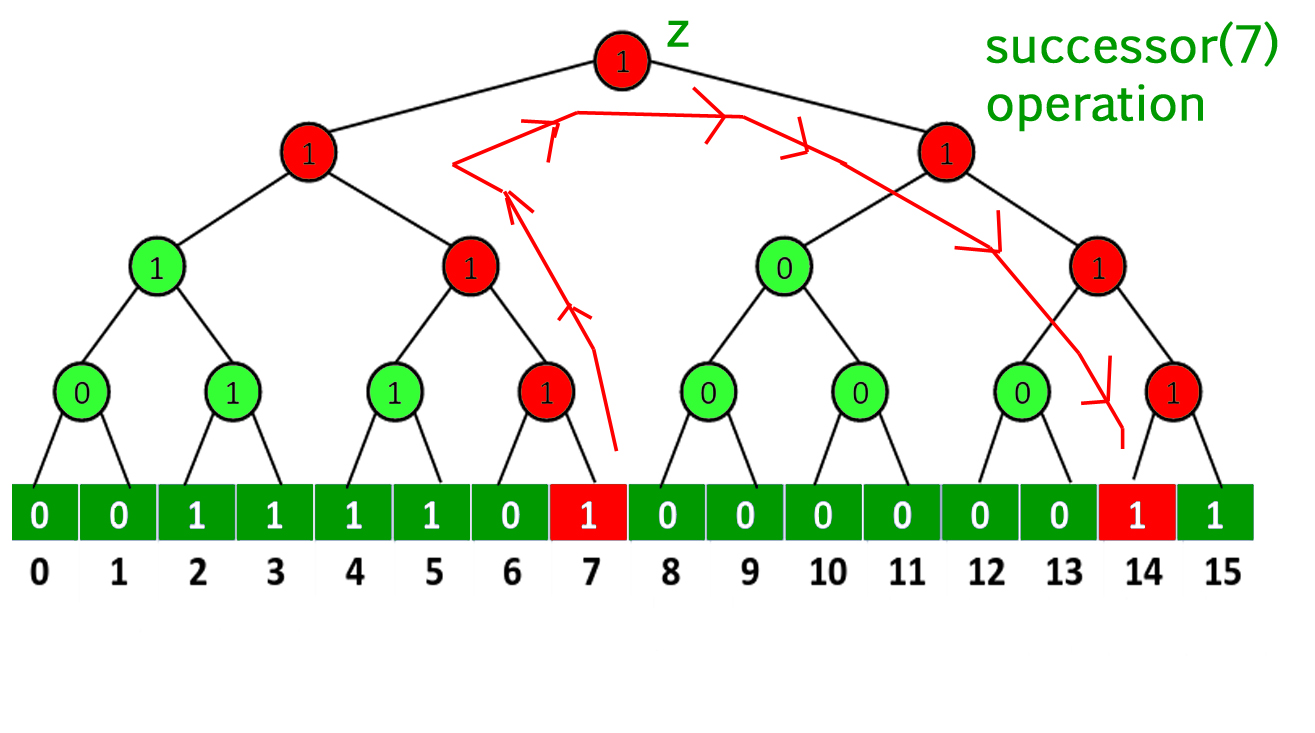
4. predecesor() : Esta operación es similar al sucesor. Aquí reemplazamos izquierda con derecha y derecha con izquierda en sucesor().
5. find() sigue siendo O (1) ya que todavía tenemos una array binaria como hojas. insert() y delete() ahora son O(Log u) ya que necesitamos actualizar los Nodes internos. En caso de inserción, marcamos la hoja correspondiente como 1, recorremos hacia arriba y seguimos actualizando los ancestros a 1 si fueran 0.

 
proto van Emde Boas Tree
Hemos visto que la superposición de un árbol binario sobre una array binaria reduce la complejidad temporal de max(), min(), sucesor() y predecesor() a O(Log u). ¿Podemos reducir aún más esta complejidad de tiempo a O (Log Log u)?

La idea es tener un grado variable en diferentes niveles. El Node raíz (primer nivel) cubre todo el universo. Cada Node de segundo nivel (al lado de la raíz) cubre u ^1/2 elementos del universo. Cada Node de tercer nivel cubre ^1/4 elementos y así sucesivamente.

Con la estructura recursiva anterior, obtenemos complejidades de tiempo de las operaciones utilizando la recursividad inferior.

T(u) = T(√u) + O(1)

Solution of this recurrence is,

T(u) = O(Log Log u)

Refer this for detailed steps to 
get the above result.

Definición recursiva del árbol proto van Emde Boas:
Sea u = 2 ^{2 k} el tamaño del universo para algún k >= 0.

1. Si u = 2, entonces es un árbol de tamaño bais que contiene solo una array binaria de tamaño 2.
2. De lo contrario, divida el universo en Θ(u ^1/2 ) bloques de tamaño Θ(u ^1/2 ) cada uno y agregue una estructura de resumen en la parte superior.

Realizamos todas las consultas utilizando el enfoque descrito en segundo plano.

En esta publicación, hemos introducido la idea de superponer la estructura de árbol en Binary Array de modo que los Nodes de diferentes niveles del árbol tengan diferentes grados. Pronto estaremos discutiendo lo siguiente en los próximos sets.
1) Representación detallada.
2) ¿Cómo optimizar max() y min() para que funcionen en O(1)?
3) Realización de las operaciones anteriores.

Fuentes:
http://www-di.inf.puc-rio.br/~laber/vanEmdeBoas.pdf
http://web.stanford.edu/class/cs166/lectures/14/Small14.pdf

Este artículo es una contribución de Shubham Agrawal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.