Prueba de cola superior de proporción de población en R

Una prueba de hipótesis estadística es un método de inferencia estadística que se utiliza para decidir si los datos disponibles respaldan suficientemente una hipótesis en particular. Los pasos convencionales que se siguen al formular la prueba de hipótesis, se enumeran a continuación

• Enunciar hipótesis nula (Ho) e hipótesis alternativa (Ha)
• Recopile una muestra relevante de datos para probar la hipótesis.
• Elija un nivel de significación para la prueba de hipótesis.
• Realice una prueba estadística adecuada.
• Con base en las estadísticas de prueba y el valor p, decida si rechazar o no rechazar su hipótesis nula.

En este artículo, analicemos cómo realizar una prueba de proporción de población de cola superior. Una prueba de cola superior es una prueba de una cola en la que el área crítica de una distribución es unilateral y prueba si la estadística de prueba es mayor que el valor crítico.

Tomemos un ejemplo más realista, supongamos que el 15% de los clientes potenciales se convirtieron en clientes en los últimos 6 meses para una empresa de venta de cupones. 18 de 250 clientes potenciales se han convertido en clientes en la mitad del ciclo actual de 6 meses. Con un nivel de significación de 0,05, probemos una hipótesis para determinar si podemos rechazar la hipótesis nula de que la proporción de conversión de clientes potenciales será inferior al 15 % durante el período restante del ciclo de 6 meses.

Hipótesis Nula: El % de conversión de leads es menor o igual al 12%. p <= po (Aquí, po = 0.12)

Hipótesis alternativa: el % de conversión de prospectos es superior al 12 %. p > po

alfa: 0.05

Definamos el estadístico de prueba de la siguiente manera

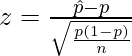
dónde,

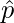•  : proporción de la muestra
• p = proporción de la población

Calculemos el estadístico de prueba como se muestra a continuación,

pbar = 18/250 # sample proportion 
p0 = .15 # hypothesized value 
n = 250 # sample size 
z = (pbar-p0)/sqrt(p0*(1-p0)/n) 
z # test statistic

Producción:

-3.45389805360637

Ahora calculemos los valores críticos,

alpha = .05 
z.alpha = qnorm(1-alpha) 
z.alpha # critical value

Producción:

1.6449

De los resultados de la prueba, podemos concluir que la estadística de prueba -3.45389805360637 es menor que el valor crítico de 1.6449. Por lo tanto, con un nivel de significación de 0,05, no podemos rechazar la hipótesis nula de que la proporción de conversión de prospectos a clientes será menor o igual al 15 % en el ciclo actual de 6 meses.