Pruebas de correlación de Kendall en programación R

La correlación es una medida estadística que indica qué tan fuertemente están relacionadas dos variables. También implica la relación entre múltiples variables. Por ejemplo, si uno está interesado en saber si existe una relación entre las alturas de padres e hijos, se puede calcular un coeficiente de correlación para responder a esta pregunta. Generalmente se encuentra entre -1 y +1. Es una versión escalada de covarianza y proporciona dirección y fuerza de relación. No tiene dimensiones. Existen principalmente dos tipos de correlación:

• Correlación Paramétrica – Correlación de Pearson(r) : Mide una dependencia lineal entre dos variables (x e y) se conoce como prueba de correlación paramétrica porque depende de la distribución de los datos.
• Correlación no paramétrica : Kendall (tau) y Spearman (rho) : son coeficientes de correlación basados ​​​​en rangos, se conocen como correlación no paramétrica.

Fórmula del coeficiente de correlación de clasificación de Kendall

Kendall Rank Correlation son coeficientes de correlación basados ​​en rangos, también conocidos como correlación no paramétrica. La fórmula para calcular la correlación de rango de Kendall es la siguiente:

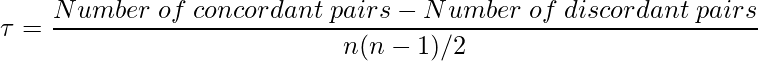
dónde,

• Par Concordante: Un par de observaciones (x1, y1) y (x2, y2) que sigue la propiedad
  • x1 > x2 y y1 > y2 o
  • x1 < x2 y y1 < y2
• Par Discordante: Un par de observaciones (x1, y1) y (x2, y2) que sigue la propiedad
  • x1 > x2 y y1 < y2 o
  • x1 < x2 y y1 > y2
• n: Número total de muestras

Nota: Se ignoran los pares para los que x1 = x2 e y1 = y2 no se clasifican como concordantes o discordantes.

Implementación en R

R Language proporciona dos métodos para calcular el coeficiente de correlación. Mediante el uso de las funciones cor() o cor.test()se puede calcular. Se puede observar que cor()calcula el coeficiente de correlación mientras que cor.test()calcula la prueba de asociación o correlación entre muestras pareadas. Devuelve tanto el coeficiente de correlación como el nivel de significancia (o valor p) de la correlación.

Sintaxis:
cor(x, y, método = “kendall”)
cor.test(x, y, método = “kendall”)

Parámetros:
x, y: vectores numéricos con la misma longitud
método: método de correlación

Ejemplo 1:

# Usando el cor()método
Ejemplo:

# R program to illustrate 
# Kendall Correlation Testing 
# Using cor() 
  
# Taking two numeric 
# Vectors with same length 
x = c(1, 2, 3, 4, 5, 6, 7)  
y = c(1, 3, 6, 2, 7, 4, 5) 
  
# Calculating  
# Correlation coefficient 
# Using cor() method 
result = cor(x, y, method = "kendall") 
  
# Print the result 
cat("Kendall correlation coefficient is:", result) 

Producción:

Kendall correlation coefficient is: 0.4285714

# Usando el cor.test()método
Ejemplo:

# R program to illustrate 
# Kendall Correlation Testing 
# Using cor.test() 
  
# Taking two numeric 
# Vectors with same length 
x = c(1, 2, 3, 4, 5, 6, 7)  
y = c(1, 3, 6, 2, 7, 4, 5) 
  
# Calculating  
# Correlation coefficient 
# Using cor.test() method 
result = cor.test(x, y, method = "kendall") 
  
# Print the result 
print(result) 

Producción:

Kendall's rank correlation tau

data:  x and y
T = 15, p-value = 0.2389
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.4285714 

En la salida anterior:

• T es el valor del estadístico de prueba (T = 15)
• El valor p es el nivel de significación de la estadística de prueba (valor p = 0,2389).
• hipótesis alternativa es una string de caracteres que describe la hipótesis alternativa (la tau verdadera no es igual a 0).
• estimaciones de la muestra es el coeficiente de correlación. Para el coeficiente de correlación de Kendall, se denomina tau (Cor.coeff = 0,4285).

Ejemplo 2:

Datos: Descarga el archivo CSV aquí .
Ejemplo:

# R program to illustrate 
# Kendall Correlation Testing 
  
# Import data into RStudio 
df = read.csv("Auto.csv") 
  
# Taking two column 
# Vectors with same length 
x = df$mpg 
y = df$weight 
  
  
# Calculating 
# Correlation coefficient 
# Using cor() method 
result = cor(x, y, method = "kendall") 
  
# Print the result 
cat("Kendall correlation coefficient is:", result) 
  
# Using cor.test() method 
res = cor.test(x, y, method = "kendall") 
print(res) 

Producción:

Kendall correlation coefficient is: -0.7517463
    Kendall's rank correlation tau

data:  x and y
z = -19.161, p-value < 2.2e-16
alternative hypothesis: true tau is not equal to 0
sample estimates:
       tau 
-0.7517463