Pruebas de hipótesis en programación R

Los investigadores formulan una hipótesis sobre los datos recopilados para cualquier experimento o conjunto de datos. Una hipótesis es una suposición hecha por los investigadores que no es obligatoriamente cierta. En palabras simples, una hipótesis es una decisión tomada por los investigadores con base en los datos de la población recolectada. La prueba de hipótesis en la programación R es un proceso para probar la hipótesis formulada por el investigador o para validar la hipótesis. Para realizar la prueba de hipótesis, se toma una muestra aleatoria de datos de la población y se realiza la prueba. Según los resultados de las pruebas, la hipótesis se selecciona o se rechaza. Este concepto se conoce como Inferencia Estadística.. En este artículo, analizaremos el proceso de cuatro pasos de la prueba de hipótesis, la prueba T de una muestra, la prueba T de dos muestras, la hipótesis direccional, la prueba de una muestra , la prueba de dos muestras y la prueba de correlación en la programación R.

Proceso de cuatro pasos de la prueba de hipótesis

Hay 4 pasos principales en la prueba de hipótesis:

• Establezca la hipótesis : este paso se inicia declarando hipótesis nula y alternativa que se presume como verdadera.
• Formule un plan de análisis y establezca los criterios para la decisión. En este paso, se establece el nivel de significancia de la prueba. El nivel de significación es la probabilidad de un falso rechazo en una prueba de hipótesis.
• Analizar datos de muestra : en esto, se utiliza una estadística de prueba para formular la comparación estadística entre la media de la muestra y la media de la población o la desviación estándar de la muestra y la desviación estándar de la población.
• Interpretar decisión : el valor de la estadística de prueba se utiliza para tomar la decisión en función del nivel de significación. Por ejemplo, si el nivel de significación se establece en 0,1 de probabilidad, se rechazará la media muestral inferior al 10 %. De lo contrario, la hipótesis se mantiene como verdadera.

Prueba T de una muestra

Un enfoque de prueba T de muestra recopila una gran cantidad de datos y los prueba en muestras aleatorias. Para realizar la prueba T en R, se requieren datos normalmente distribuidos. Esta prueba se utiliza para contrastar la media de la muestra con la población. Por ejemplo, la altura de las personas que viven en un área es diferente o idéntica a la de otras personas que viven en otras áreas.

Sintaxis: t.test(x, mu)

Parámetros:
x: representa el vector numérico de datos

mu: representa el valor verdadero de la media

Para conocer más parámetros opcionales de t.test() , pruebe el siguiente comando:

help("t.test")

Ejemplo:

# Defining sample vector
x <- rnorm(100)
  
# One Sample T-Test
t.test(x, mu = 5)

Producción:

    One Sample t-test

data:  x
t = -49.504, df = 99, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
 -0.1910645  0.2090349
sample estimates:
  mean of x 
0.008985172 

Prueba T de dos muestras

En la prueba T de dos muestras, se comparan los vectores de muestra. Si var.equal = TRUE, la prueba asume que las varianzas de ambas muestras son iguales.

Sintaxis: t.test(x, y)

Parámetros:
x e y: Vectores numéricos

Ejemplo:

# Defining sample vector
x <- rnorm(100)
y <- rnorm(100)
  
# Two Sample T-Test
t.test(x, y)

Producción:

        Welch Two Sample t-test

data:  x and y
t = -1.0601, df = 197.86, p-value = 0.2904
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.4362140  0.1311918
sample estimates:
  mean of x   mean of y 
-0.05075633  0.10175478 

Hipótesis direccional

Usando la hipótesis direccional, la dirección de la hipótesis se puede especificar si el usuario quiere saber si la media de la muestra es menor o mayor que otra muestra media de los datos.

Sintaxis: t.test(x, mu, alternativa)

Parámetros:
x: representa datos vectoriales numéricos

mu: representa la media contra la cual se deben probar los datos de la muestra

alternativa: establece la hipótesis alternativa

Ejemplo:

# Defining sample vector
x <- rnorm(100)
  
# Directional hypothesis testing
t.test(x, mu = 2, alternative = 'greater')

Producción:

        One Sample t-test

data:  x
t = -20.708, df = 99, p-value = 1
alternative hypothesis: true mean is greater than 2
95 percent confidence interval:
 -0.2307534        Inf
sample estimates:
 mean of x 
-0.0651628 

Una muestra 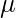 – Prueba

Este tipo de prueba se utiliza cuando la comparación debe calcularse en una muestra y los datos no son paramétricos. Se realiza usando wilcox.test() la función en la programación R.

Sintaxis: wilcox.test(x, y, exacta = NULL)

Parámetros:
x e y: representa un vector numérico

exacto: representa el valor lógico que indica si se calculará el valor p

Para conocer más parámetros opcionales de wilcox.test() , use el siguiente comando:

help("wilcox.test")

Ejemplo:

# Define vector
x <- rnorm(100)
  
# one sample test
wilcox.test(x, exact = FALSE)

Producción:

        Wilcoxon signed rank test with continuity correction

data:  x
V = 2555, p-value = 0.9192
alternative hypothesis: true location is not equal to 0

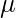Prueba de dos muestras 

Esta prueba se realiza para comparar dos muestras de datos.

Ejemplo:

# Define vectors
x <- rnorm(100)
y <- rnorm(100)
  
# Two sample test
wilcox.test(x, y)

Producción:

        Wilcoxon rank sum test with continuity correction

data:  x and y
W = 5300, p-value = 0.4643
alternative hypothesis: true location shift is not equal to 0

Prueba de correlación

Esta prueba se utiliza para comparar la correlación de los dos vectores proporcionados en la llamada de función o para probar la asociación entre las muestras emparejadas.

Sintaxis: cor.test(x, y)

Parámetros:
x e y: representan vectores de datos numéricos

Para conocer más parámetros opcionales en la función cor.test() , use el siguiente comando:

help("cor.test")

Ejemplo:

# Using mtcars dataset in R
cor.test(mtcars$mpg, mtcars$hp)

Producción:

        Pearson's product-moment correlation

data:  mtcars$mpg and mtcars$hp
t = -6.7424, df = 30, p-value = 1.788e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.8852686 -0.5860994
sample estimates:
       cor 
-0.7761684