Prueba U de Mann Whitney en Programación R

Una prueba popular no paramétrica (sin distribución) para comparar resultados entre dos grupos independientes es la prueba U de Mann Whitney . Cuando se comparan dos muestras independientes, cuando el resultado no tiene una distribución normal y las muestras son pequeñas, es adecuada una prueba no paramétrica. Se utiliza para ver la diferencia de distribución entre dos variables independientes sobre la base de una variable dependiente ordinal (variable categórica que tiene un orden o rango intrínseco). Es muy fácil realizar esta prueba en programación R.

Implementación de la Prueba U de Mann Whitney en Programación R

Digamos que tenemos dos tipos de bombillas naranja y roja en nuestros datos y estos se dividen en los precios base diarios. Así que aquí los precios base son variables dependientes de las dos categorías que son rojo y naranja. Por lo tanto, intentaremos analizar si queremos comprar una bombilla de color rojo o naranja, ¿cuál deberíamos preferir en función de los precios? Si ambas distribuciones son iguales, esto significa que la hipótesis nula ( significa que no hay una diferencia significativa entre las dos ) es verdadera y podemos comprar cualquiera de ellas y los precios no importarán. Para comprender el concepto de la prueba U de Mann Whitney, es necesario saber cuál es el valor p . Este valor realmente dice si podemos rechazar nuestra hipótesis nula (0.5) o no. A continuación se muestra la implementación del ejemplo anterior. 

Acercarse

1.  Cree un marco de datos con dos variables categóricas en las que una sería de tipo ordinal.
2. Después de esto, verifique el resumen de la variable categórica no ordinal cargando un paquete dplyr y obtenga los valores medianos usando y pasando la columna bulb_prices, el rango intercuartílico de IQR y el recuento de ambos grupos, es decir , bombilla roja y naranja .
3. Luego mire el diagrama de caja y vea la distribución de los datos con la ayuda de instalar un paquete ggpubr y usar y pasar las columnas como argumentos en x e y y darles color con la ayuda de la paleta y pasar los códigos de color.
4. Luego, finalmente aplique la función para obtener el valor p .
5. Si se encuentra que el valor p es inferior a 0,5 , se rechazará la hipótesis nula .
6. Si encontramos que el valor es mayor a 0.5 entonces se aceptará la hipótesis nula .
7. La función toma ambas variables categóricas, dataframe como argumento, y nos da el valor de la hipótesis .

# R program to illustrate
# Mann Whitney U Test
 
# Creating a small dataset
# Creating a vector of red bulb and orange prices
red_bulb <- c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8)
orange_bulb <- c(47.8, 60, 63.4, 76, 89.4, 67.3, 61.3, 62.4)
 
# Passing them in the columns
BULB_PRICE = c(red_bulb, orange_bulb)
BULB_TYPE = rep(c("red", "orange"), each = 8)
 
# Now creating a dataframe
DATASET <- data.frame(BULB_TYPE, BULB_PRICE, stringsAsFactors = TRUE)
 
# printing the dataframe
DATASET
 
# installing libraries to view summaries and
# boxplot of both orange and red color bulbs
install.packages("dplyr")
install.packages("ggpubr")
 
# Summary of the data
 
# loading the package
library(dplyr)
group_by(DATASET,BULB_TYPE) %>%
  summarise(
    count = n(),
    median = median(BULB_PRICE, na.rm = TRUE),
    IQR = IQR(BULB_PRICE, na.rm = TRUE))
 
# loading package for boxplot
library("ggpubr")
ggboxplot(DATASET, x = "BULB_TYPE", y = "BULB_PRICE",
          color = "BULB_TYPE", palette = c("#FFA500", "#FF0000"),
          ylab = "BULB_PRICES", xlab = "BULB_TYPES")
 
res <- wilcox.test(BULB_PRICE~ BULB_TYPE,
                   data = DATASET,
                   exact = FALSE)
res

 Producción:

> CONJUNTO DE DATOS

     BULB_TYPE BULB_PRICE
1        red       38.9
2        red       61.2
3        red       73.3
4        red       21.8
5        red       63.4
6        red       64.6
7        red       48.4
8        red       48.8
9     orange       47.8
10    orange       60.0
11    orange       63.4
12    orange       76.0
13    orange       89.4
14    orange       67.3
15    orange       61.3
16    orange       62.4

# resumen de los datos

summarise()` ungrouping output (override with `.groups` argument)
# A tibble: 2 x 4
  BULB_TYPE count median   IQR
  <fct>     <int>  <dbl> <dbl>
1 orange        8   62.9   8.5
2 red           8   55    17.7

# diagrama de caja

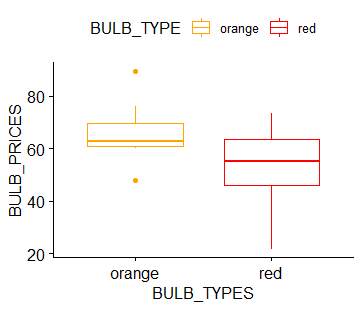
> resolución

        Wilcoxon rank sum test with continuity correction

data:  BULB_PRICE by BULB_TYPE
W = 44.5, p-value = 0.2072
alternative hypothesis: true location shift is not equal to 0

Explicación:

Aquí, como podemos ver, el valor de p resulta ser 0.2072  , que es mucho menor que la hipótesis nula (0.5) . Por lo que será rechazado. Y puede concluir que la distribución de precios entre bombillas rojas y naranjas no es la misma. Debido a lo cual no puede decir que si es rentable comprar alguna de las bombillas anteriores es rentable.