Prueba Z de una proporción en programación R

La prueba Z de una proporción se utiliza para comparar una proporción observada con una teórica cuando solo hay dos categorías. Por ejemplo, tenemos una población de ratones que contiene la mitad de machos y la mitad de hembras (p = 0,5 = 50%). Algunos de estos ratones (n = 160) desarrollaron cáncer espontáneo, incluidos 95 machos y 65 hembras. Queremos saber si el cáncer afecta más a los hombres que a las mujeres. Entonces en este problema:

• El número de éxitos (hombre con cáncer) es 95
• La proporción observada (p _o ) del macho es 95/160
• La proporción observada (q) de la hembra es 1 – p _o
• La proporción esperada (p _e ) del macho es 0.5 (50%)
• El número de observaciones (n) es 160

La fórmula para la prueba Z de una proporción

La estadística de prueba (también conocida como prueba z) se puede calcular de la siguiente manera:

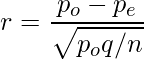
dónde,

p _o : la proporción observada
q: 1 – p _o
p _e : la proporción esperada
n: el tamaño de la muestra

Implementación en R

En R Language , la función utilizada para realizar una prueba z es binom.test()y prop.test().

Sintaxis:
binom.test(x, n, p = 0.5, alternativa = “dos caras”)
prop.test(x, n, p = NULL, alternativa = “dos caras”, correcto = VERDADERO)

Parámetros:
x = número de éxitos y fracasos en el conjunto de datos.
n = tamaño del conjunto de datos.
p = probabilidades de éxito. Debe estar en el rango de 0 a 1.
alternativa = una string de caracteres que especifica la hipótesis alternativa.
correcto = una indicación lógica de si se debe aplicar la corrección de continuidad de Yates cuando sea posible.

Ejemplo 1:
Supongamos que 30 de 70 personas recomiendan Street Food a sus amigos. Para probar esta afirmación, se obtuvo una muestra aleatoria de 150 personas. De estas 150 personas, 80 indican que recomiendan Street Food a su amigo. ¿Es correcta esta afirmación? Utilice alfa = 0,05.

Solución:
Ahora dado x=.80, P=.30, n=150. Queremos saber si la gente recomienda comida callejera a su amigo en lugar de comida saludable. Usemos la función prop.test()en R.

# Using prop.test()
prop.test(x = 80, n = 150, p = 0.3,  
                  correct = FALSE)

Producción:

        1-sample proportions test without continuity correction
data:  80 out of 150, null probability 0.3
X-squared = 38.889, df = 1, p-value = 4.489e-10
alternative hypothesis: true p is not equal to 0.3
95 percent confidence interval:
0.4536625 0.6113395
sample estimates:
       p  
0.5333333

• Devuelve el valor p que es 4.186269
• hipótesis alternativa.
• intervalos de confianza del 95%.
• la probabilidad de éxito es 0.53

El valor p de la prueba es 4,486269, que es menor que el nivel de significación alfa = 0,05. La afirmación de que 30 de 70 personas recomiendan Street Food a sus amigos no es precisa.

Ejemplo 2:
Suponga que las píldoras de vitaminas actuales curan el 80% de todos los casos. Se ha descubierto o fabricado una nueva píldora de vitaminas. En una muestra de 150 pacientes con carencia de vitaminas que fueron tratados con las nuevas vitaminas, 95 se curaron. ¿Los resultados de este estudio respaldan la afirmación de que las nuevas vitaminas tienen una tasa de curación más alta que las vitaminas existentes?

Solución:
Ahora dado x=.95, P=.80, n=160. Usemos la función prop.test()en R.

# Using prop.test() 
prop.test(x = 95, n = 160, p = 0.8,  
                 correct = FALSE)

Producción:

 
        1-sample proportions test without continuity correction
data:  95 out of 160, null probability 0.8
X-squared = 42.539, df = 1, p-value = 6 . 928e-11
alternative hypothesis: true p is not equal to 0.8
95 percent confidence interval:
0.5163169 0.6667870
sample estimates:
     p  
0.59375

• Devuelve el valor p que es 6.928462
• hipótesis alternativa
• intervalos de confianza del 95%.
• la probabilidad de éxito es 0.59

El valor p de la prueba es 6,928462, que es mayor que el nivel de significación alfa = 0,05. La afirmación de que 95 de 160 personas se curaron con nuevas vitaminas es correcta.

Ejemplo 3:
Suponga que en India al 15% de las personas les gusta trabajar desde casa. En una muestra de 100 personas, las personas a las que les gusta trabajar desde casa son 25. ¿Es correcta esta afirmación?

Solución:
Ahora dado x=.25, P=.15, n=100. Usemos la función binom.test()en R.

# Using binom.test()
binom.test(x =25, n = 100, p = 0.15)

Producción:

Exact binomial test

data:  25 and 100
number of successes = 25, number of trials = 100, p-value = 0.007633
alternative hypothesis: true probability of success is not equal to 0.15
95 percent confidence interval:
 0.1687797 0.3465525
sample estimates:
probability of success 
                  0.25 

• Devuelve el valor p que es 0.007633
• hipótesis alternativa.
• intervalos de confianza del 95%.
• la probabilidad de éxito es 0.25

El valor p de la prueba es 0,007633, que es menor que el nivel de significación alfa = 0,05. La afirmación de que a 25 de cada 100 personas les gusta trabajar desde casa no es precisa.