Los algoritmos de clasificación son los medios para clasificar un conjunto dado de datos en un orden de acuerdo con los requisitos del usuario. Se utilizan principalmente para ordenar datos de manera creciente o decreciente. Hay dos tipos de algoritmos de clasificación:
- Algoritmos de clasificación basados en comparación
- Algoritmos de clasificación no basados en la comparación
Algoritmos de clasificación basados en comparación : los elementos de una array se comparan entre sí para clasificar la array. Este tipo de algoritmo verifica si un elemento es mayor o igual que otro elemento en la array. No manipula un solo elemento de array.
Ejemplos de algoritmos basados en la comparación : ordenación por combinación (compara los elementos y cópialos ), ordenación rápida (compara los elementos e intercámbialos) y ordenación en montón (apila los elementos usando la comparación).
Teorema : cada algoritmo de clasificación basado en comparación tiene el peor tiempo de ejecución de
Prueba:
Supongamos un algoritmo de clasificación basado en comparación y una array de longitud N . Considere que la array de entrada contiene elementos de array como ![]() en un orden desordenado. ¡Podemos ordenar estos N elementos en N! diferentes caminos.
en un orden desordenado. ¡Podemos ordenar estos N elementos en N! diferentes caminos.
- Suposiciones:
- El primer elemento tiene N formas de ordenar, el segundo elemento tiene (N – 1) formas de ordenar, el tercer elemento tiene (N – 2) formas, y así sucesivamente.
Entonces, ¡estos elementos se pueden ordenar en N! maneras. - Supongamos que el número de comparaciones que hace este algoritmo en el peor de los casos para organizar es K , es decir, el número máximo de comparaciones en la array de entrada de tamaño N es K . Para ordenar correctamente todos los N! El algoritmo de entradas posibles exhibe distintas ejecuciones.
- El primer elemento tiene N formas de ordenar, el segundo elemento tiene (N – 1) formas de ordenar, el tercer elemento tiene (N – 2) formas, y así sucesivamente.
- Demostración: Por el principio de Pigeonhole : si se colocan n elementos en mcontenedores, con n > m , entonces al menos un contenedor debe contener más de un artículo.
- ¡ Aquí, la paloma es N! diferentes entradas. Los agujeros son de 2 K ejecuciones diferentes.
- Si
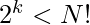 , esto significa que el algoritmo se ejecuta de manera idéntica en 2 entradas distintas, y no podemos tener una ejecución común del algoritmo de clasificación, lo cual es contrario a nuestra suposición de un algoritmo de clasificación.
, esto significa que el algoritmo se ejecuta de manera idéntica en 2 entradas distintas, y no podemos tener una ejecución común del algoritmo de clasificación, lo cual es contrario a nuestra suposición de un algoritmo de clasificación. - Dado que el método de clasificación es correcto, 2 K ≥ N! ≥ (N/2) N/2 , donde hemos usado el hecho de que los primeros N/2 términos de N*(N – 1)* … 2*1 son al menos N/2.
- Tomando logaritmo en base 2 en ambos lados, K = (N/2)log 2 (N/2)
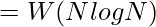
- Por lo tanto, cada algoritmo de clasificación basado en comparación tiene el peor tiempo de ejecución que nunca puede ser mejor que
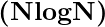 .
.
Para más detalles, consulte:
Diseño y Análisis de Algoritmos .
Publicación traducida automáticamente
Artículo escrito por shreelakshmijoshi1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA