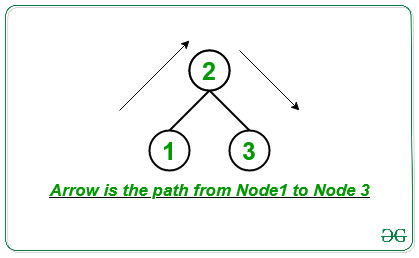
Dado un número entero N que denota el número de ciudades conectadas ( numeradas de 1 a N ) y una array 2D arr[][] que consta de pares conectados entre sí por puentes bidireccionales. La tarea es encontrar el número mínimo de puentes necesarios para cruzar para llegar a la ciudad N desde la ciudad 1 .
Ejemplos:
Entrada: N = 3, M = 2, array[][] = {{1, 2}, {2, 3}}
Salida: 2
Explicación:
Para llegar al Node 2 desde el Node 1, se requiere cruzar 1 puente.
Para llegar al Node 3 desde el Node 2, se requiere cruzar 1 puente.
Por lo tanto, se requieren 2 puentes para estar conectados.Entrada: N = 4, M = 3, arr[][] = {{1, 2}, {2, 3}, {2, 4}}
Salida: 2
Enfoque: siga los pasos a continuación para resolver el problema:
- Inicialice una lista de adyacencia para construir y almacenar los Nodes de gráficos .
- Inicialice una array , digamos vis[] de tamaño N para marcar los Nodes visitados y otra array, digamos dist[] de tamaño N , para almacenar la distancia mínima desde la ciudad 1 .
- Realice BFS y utilice el concepto de ruta más corta de fuente única para recorrer el gráfico y almacenar la cantidad mínima de puentes necesarios para cruzar para llegar a cada ciudad desde la ciudad 1 .
- Imprime el valor de dist[N] como la distancia mínima para llegar a la ciudad N desde la ciudad 1 .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Adjacency list to store graph
vector<int> g[10001];
// Stores info about visited nodes
int vis[10001];
// Stores distance of nodes
// from the source node
int dist[10001];
// Function for BFS traversal
void BFS(int src)
{
// Stores the nodes
queue<int> q;
// Push the source node
q.push(src);
// Mark the pushed node visited
vis[src] = 1;
// Source node is always at dist 0
dist[src] = 0;
// Iterate until queue is not empty
while (!q.empty()) {
// Update the current node
int curr = q.front();
// Pop the node after
// update by curr
q.pop();
// Traverse every node of
// the adjacency list
for (auto child : g[curr]) {
if (vis[child] == 0) {
// Push the child node
// if its not visited
q.push(child);
// Update the distance of next level
// nodes as it can be accessed by the
// previous node in BFS
dist[child] = dist[curr] + 1;
// Mark the child node as visited
vis[child] = 1;
}
}
}
}
// Function to build the graph
void buildGraph(int M, int arr[][2])
{
for (int i = 0; i < M; i++) {
g[arr[i][0]].push_back(arr[i][1]);
g[arr[i][1]].push_back(arr[i][0]);
}
}
// Function to print the distance between from
// city 1 to city N
void shortestDistance(int N, int M, int arr[][2])
{
// Build graph
buildGraph(M, arr);
// Perform BFS traversal
BFS(1);
// Print the shortest distance
cout << dist[N];
}
// Driver Code
int main()
{
// Given number of Nodes & Edges
int N = 3, M = 2;
// Given pairs of edges
int arr[][2] = { { 1, 2 }, { 2, 3 } };
// Function Call
shortestDistance(N, M, arr);
}
Java
// Java program for the above approach
import java.util.*;
class GFG
{
// Adjacency list to store graph
static Vector<Integer> []g = new Vector[10001];
// Stores info about visited nodes
static int []vis = new int[10001];
// Stores distance of nodes
// from the source node
static int []dist = new int[10001];
static {
for(int i = 0; i < g.length; i++)
{
g[i] = new Vector<>();
}
}
// Function for BFS traversal
static void BFS(int src)
{
// Stores the nodes
Queue<Integer> q = new LinkedList<>();
// Push the source node
q.add(src);
// Mark the pushed node visited
vis[src] = 1;
// Source node is always at dist 0
dist[src] = 0;
// Iterate until queue is not empty
while (!q.isEmpty()) {
// Update the current node
int curr = q.peek();
// Pop the node after
// update by curr
q.remove();
// Traverse every node of
// the adjacency list
for (int child : g[curr]) {
if (vis[child] == 0) {
// Push the child node
// if its not visited
q.add(child);
// Update the distance of next level
// nodes as it can be accessed by the
// previous node in BFS
dist[child] = dist[curr] + 1;
// Mark the child node as visited
vis[child] = 1;
}
}
}
}
// Function to build the graph
static void buildGraph(int M, int arr[][])
{
for (int i = 0; i < M; i++) {
g[arr[i][0]].add(arr[i][1]);
g[arr[i][1]].add(arr[i][0]);
}
}
// Function to print the distance between from
// city 1 to city N
static void shortestDistance(int N, int M, int arr[][])
{
// Build graph
buildGraph(M, arr);
// Perform BFS traversal
BFS(1);
// Print the shortest distance
System.out.print(dist[N]);
}
// Driver Code
public static void main(String[] args)
{
// Given number of Nodes & Edges
int N = 3, M = 2;
// Given pairs of edges
int arr[][] = { { 1, 2 }, { 2, 3 } };
// Function Call
shortestDistance(N, M, arr);
}
}
// This code is contributed by shikhasingrajput.
Python3
# Python 3 program for the above approach # Adjacency list to store graph g = [[] for i in range(10001)] # Stores info about visited nodes vis = [0 for i in range(10001)] # Stores distance of nodes # from the source node dist = [0 for i in range(10001)] # Function for BFS traversal def BFS(src): global vis global dist global g # Stores the nodes q = [] # Push the source node q.append(src) # Mark the pushed node visited vis[src] = 1 # Source node is always at dist 0 dist[src] = 0 # Iterate until queue is not empty while (len(q)): # Update the current node curr = q[0] # Pop the node after # update by curr q.remove(q[0]) # Traverse every node of # the adjacency list for child in g[curr]: if (vis[child] == 0): # Push the child node # if its not visited q.append(child) # Update the distance of next level # nodes as it can be accessed by the # previous node in BFS dist[child] = dist[curr] + 1 # Mark the child node as visited vis[child] = 1 # Function to build the graph def buildGraph(M, arr): global g for i in range(M): g[arr[i][0]].append(arr[i][1]) g[arr[i][1]].append(arr[i][0]) # Function to print the distance between from # city 1 to city N def shortestDistance(N, M, arr): # Build graph buildGraph(M, arr) # Perform BFS traversal BFS(1) # Print the shortest distance print(dist[N]) # Driver Code if __name__ == '__main__': # Given number of Nodes & Edges N = 3 M = 2 # Given pairs of edges arr = [[1, 2], [2, 3]] # Function Call shortestDistance(N, M, arr) # This code is contributed by SURENDRA_GANGWAR.
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
public class GFG
{
// Adjacency list to store graph
static List<int> []g = new List<int>[10001];
// Stores info about visited nodes
static int []vis = new int[10001];
// Stores distance of nodes
// from the source node
static int []dist = new int[10001];
// Function for BFS traversal
static void BFS(int src)
{
// Stores the nodes
Queue<int> q = new Queue<int>();
// Push the source node
q.Enqueue(src);
// Mark the pushed node visited
vis[src] = 1;
// Source node is always at dist 0
dist[src] = 0;
// Iterate until queue is not empty
while (q.Count!=0) {
// Update the current node
int curr = q.Peek();
// Pop the node after
// update by curr
q.Dequeue();
// Traverse every node of
// the adjacency list
foreach (int child in g[curr]) {
if (vis[child] == 0) {
// Push the child node
// if its not visited
q.Enqueue(child);
// Update the distance of next level
// nodes as it can be accessed by the
// previous node in BFS
dist[child] = dist[curr] + 1;
// Mark the child node as visited
vis[child] = 1;
}
}
}
}
// Function to build the graph
static void buildGraph(int M, int [,]arr)
{
for (int i = 0; i < M; i++) {
g[arr[i,0]].Add(arr[i,1]);
g[arr[i,1]].Add(arr[i,0]);
}
}
// Function to print the distance between from
// city 1 to city N
static void shortestDistance(int N, int M, int [,]arr)
{
// Build graph
buildGraph(M, arr);
// Perform BFS traversal
BFS(1);
// Print the shortest distance
Console.Write(dist[N]);
}
// Driver Code
public static void Main(String[] args)
{
// Given number of Nodes & Edges
int N = 3, M = 2;
// Given pairs of edges
int [,]arr = { { 1, 2 }, { 2, 3 } };
for(int i = 0; i < g.Length; i++)
{
g[i] = new List<int>();
}
// Function Call
shortestDistance(N, M, arr);
}
}
// This code is contributed by shikhasingrajput
Javascript
<script>
// JavaScript program for the above approach
// Adjacency list to store graph
var g = Array.from(Array(10001), ()=>new Array());;
// Stores info about visited nodes
var vis = Array(10001).fill(false);
// Stores distance of nodes
// from the source node
var dist = Array(10001).fill(0);
// Function for BFS traversal
function BFS(src)
{
// Stores the nodes
var q = [];
// Push the source node
q.push(src);
// Mark the pushed node visited
vis[src] = 1;
// Source node is always at dist 0
dist[src] = 0;
// Iterate until queue is not empty
while (q.length!=0) {
// Update the current node
var curr = q[0];
// Pop the node after
// update by curr
q.shift();
// Traverse every node of
// the adjacency list
g[curr].forEach(child => {
if (vis[child] == 0) {
// Push the child node
// if its not visited
q.push(child);
// Update the distance of next level
// nodes as it can be accessed by the
// previous node in BFS
dist[child] = dist[curr] + 1;
// Mark the child node as visited
vis[child] = 1;
}
});
}
}
// Function to build the graph
function buildGraph(M, arr)
{
for (var i = 0; i < M; i++) {
g[arr[i][0]].push(arr[i][1]);
g[arr[i][1]].push(arr[i][0]);
}
}
// Function to print the distance between from
// city 1 to city N
function shortestDistance(N, M, arr)
{
// Build graph
buildGraph(M, arr);
// Perform BFS traversal
BFS(1);
// Print the shortest distance
document.write( dist[N]);
}
// Driver Code
// Given number of Nodes & Edges
var N = 3, M = 2;
// Given pairs of edges
var arr = [ [ 1, 2 ], [ 2, 3 ] ];
// Function Call
shortestDistance(N, M, arr);
</script>
2
Complejidad temporal: O(N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por sagnikmukherjee2 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA