Punto de inicio de hoja en una estructura de datos Binary Heap

Binary Heap es un árbol completo (todos los niveles están completamente llenos, excepto posiblemente el último nivel y el último nivel tiene todas las claves tan a la izquierda como sea posible). En otras palabras, podemos decir que es un árbol binario casi completo. Un montón binario normalmente se representa como una array. Si miramos más de cerca, podemos notar que en un Heap con un número de Nodes n, las hojas parten de un índice particular y, siguiéndolo, todos los Nodes son hojas hasta el índice n. Veamos un ejemplo para observar esto:

            10 
         /      \               
       20        100          
      /                      
    30                     

Representemos esto en forma de un arreglo Arr cuyo índice parte de 1: tenemos: Arr[1] = 10 Arr[2] = 20 Arr[3] = 100 Arr[4] = 30 Si observamos, el primer leaf (es decir, 100) comienza desde el índice 3. Siguiéndolo, Arr[4] también es una hoja. Al analizar cuidadosamente, se observa la siguiente conclusión:

La primera hoja de un Heap comienza en [piso(n/2)]+1 y todos los Nodes que le siguen hasta n son hojas.

Conclusión: en un montón que tiene n elementos, los elementos de los índices [(piso (n/2) + 1) a n] son ​​hojas. ¿Cuál es el índice inicial de las hojas si los índices comienzan desde 0 en lugar de 1? La explicación anterior asume índices a partir de 1, pero en la mayoría de los lenguajes de programación, el índice comienza con 0. 

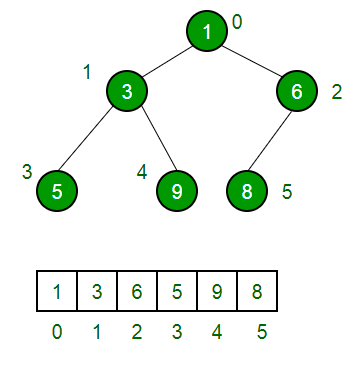
Si consideramos 0 como índice inicial, las hojas comienzan desde el piso (n/2) y existen hasta el final, es decir, (n-1).

Este artículo es una contribución de Ranju Kumari . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.