Algoritmo Push Relabel | Conjunto 1 (Introducción e Ilustración)

Dado un gráfico que representa una red de flujo donde cada borde tiene una capacidad. También dados dos vértices fuente ‘s’ y sumidero ‘t’ en el gráfico, encuentre el flujo máximo posible de s a t con las siguientes restricciones:

El flujo en un borde no excede la capacidad dada del borde.
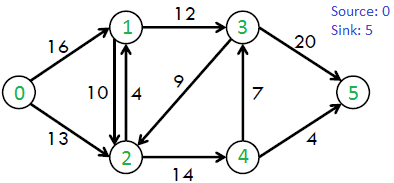
El flujo entrante es igual al flujo saliente para cada vértice excepto s y t. Por ejemplo, considere el siguiente gráfico del libro CLRS.

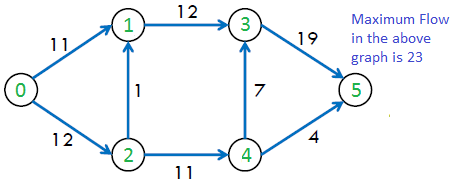
El caudal máximo posible en el gráfico anterior es 23.

Hemos discutido el algoritmo de Ford Fulkerson que utiliza una ruta de aumento para calcular el flujo máximo.

Algoritmo Push-Relabel

El enfoque Push-Relabel es más eficiente que el algoritmo Ford-Fulkerson. En esta publicación, se analiza el algoritmo de flujo máximo «genérico» de Goldberg que se ejecuta en el tiempo O (V ² E) . Esta complejidad de tiempo es mejor que O(E ² V), que es la complejidad de tiempo del algoritmo de Edmond-Karp (una implementación basada en BFS de Ford-Fulkerson). Existe un algoritmo basado en el enfoque push-relabel que funciona en O(V ³ ) que es incluso mejor que el que se analiza aquí. Similitudes con Ford Fulkerson

Al igual que Ford-Fulkerson, Push-Relabel también funciona en el gráfico residual (el gráfico residual de una red de flujo es un gráfico que indica un flujo adicional posible. Si hay una ruta desde la fuente hasta el sumidero en el gráfico residual, entonces es posible agregar flujo) .

Diferencias con Ford Fulkerson

El algoritmo Push-relabel funciona de una forma más localizada. En lugar de examinar toda la red residual para encontrar una ruta de aumento, los algoritmos push-relabel funcionan en un vértice a la vez (Fuente: Libro CLRS).
En Ford-Fulkerson, la diferencia neta entre el flujo de salida total y el flujo de entrada total para cada vértice (excepto fuente y sumidero) se mantiene en 0. El algoritmo Push-Relabel permite que el flujo de entrada supere el flujo de salida antes de alcanzar el flujo final. En el flujo final, la diferencia neta es 0 para todos excepto para la fuente y el sumidero.
La complejidad del tiempo es más eficiente.

La intuición detrás del algoritmo push-relabel (considerando un problema de flujo de fluido) es que consideramos los bordes como tuberías de agua y los Nodes son juntas. Se considera que la fuente está en el nivel más alto y envía agua a todos los Nodes adyacentes. Una vez que un Node tiene exceso de agua, empuja el agua a un Node de menor altura. Si el agua queda atrapada localmente en un vértice, el vértice se vuelve a etiquetar , lo que significa que su altura aumenta. Los siguientes son algunos hechos útiles a considerar antes de proceder con el algoritmo.

Cada vértice tiene asociada una variable de altura y un Exceso de Caudal. La altura se usa para determinar si un vértice puede empujar el flujo hacia un vértice adyacente o no (un vértice puede empujar el flujo solo hacia un vértice de menor altura). El exceso de flujo es la diferencia del flujo total que ingresa al vértice menos el flujo total que sale del vértice.

     Excess Flow of u = Total Inflow to u - 
                        Total Outflow from u

Como Ford Fulkerson. cada arista tiene asociado un caudal (que indica caudal de corriente) y una capacidad

Los siguientes son pasos abstractos del algoritmo completo.

Push-Relabel Algorithm 
1) Initialize PreFlow : Initialize Flows 
   and Heights 

2) While it is possible to perform a Push() or 
   Relabel() on a vertex
   // Or while there is a vertex that has excess flow
           Do Push() or Relabel()

// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.

Hay tres operaciones principales en el algoritmo Push-Relabel

Initialize PreFlow() Inicializa alturas y flujos de todos los vértices.

Preflow() 
1) Initialize height and flow of every vertex as 0.
2) Initialize height of source vertex equal to total 
   number of vertices in graph.
3) Initialize flow of every edge as 0.
4) For all vertices adjacent to source s, flow and  
   excess flow is equal to capacity initially.

Push() se usa para hacer que el flujo fluya desde un Node que tiene exceso de flujo. Si un vértice tiene exceso de flujo y hay un adyacente con menor altura (en el gráfico residual), empujamos el flujo del vértice al adyacente con menor altura. La cantidad de flujo empujado a través de la tubería (borde) es igual al mínimo de exceso de flujo y capacidad del borde.
La operación Relabel() se usa cuando un vértice tiene exceso de flujo y ninguno de sus adyacentes está a menor altura. Básicamente, aumentamos la altura del vértice para que podamos realizar push(). Para aumentar la altura, elegimos la altura mínima adyacente (en el gráfico residual, es decir, un adyacente al que podemos agregar flujo) y le sumamos 1.

Tenga en cuenta que las operaciones anteriores se realizan en el gráfico residual (como Ford-Fulkerson ).

Ilustración:

Antes de continuar con el siguiente ejemplo, debemos asegurarnos de que entendemos el gráfico residual (consulte esto para obtener más detalles del gráfico residual). El gráfico residual es diferente de los gráficos que se muestran.
Cada vez que empujamos o agregamos un flujo de un vértice u a v, hacemos las siguientes actualizaciones en el gráfico residual:

Restamos el flujo de la capacidad del borde de u a v. Si la capacidad de un borde se convierte en 0, entonces el borde ya no existe en el gráfico residual.
Agregamos flujo a la capacidad del borde de v a u.

For example, consider two vertices u an v.

In original graph
        3/10
   u ---------> v
    3 is current flow from u to v and
    10 is capacity of edge from u to v.

In residual Graph, there are two edges corresponding
to one edge shown above.
         7
   u ---------> v

         3
   u <--------- v

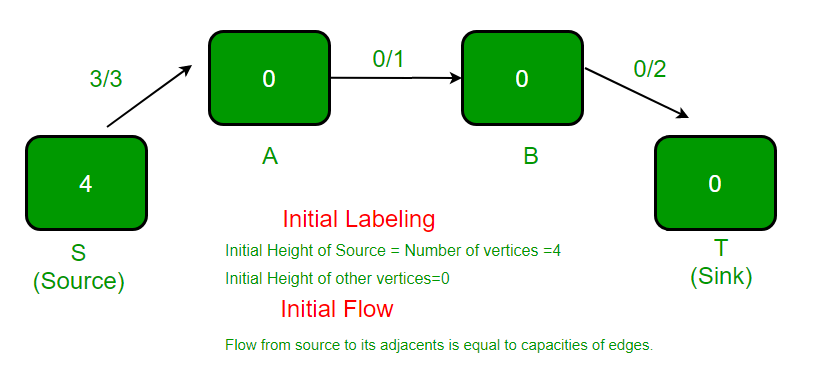
Diagrama de flujo dado inicial.
Después de la operación PreFlow. En el gráfico residual, hay un borde de A a S con capacidad 3 y ningún borde de S a A.
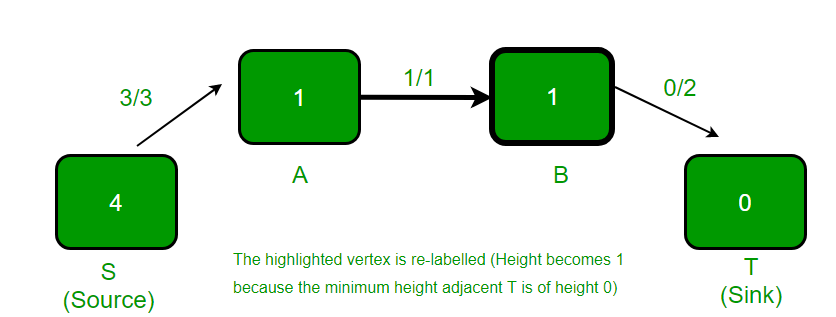
El vértice resaltado se vuelve a etiquetar (la altura se convierte en 1) ya que tiene exceso de flujo y no hay ningún adyacente con menor altura. La nueva altura es igual al mínimo de las alturas de los adyacentes más 1. En el gráfico residual, hay dos adyacentes del vértice A, uno es S y otro es B. La altura de S es 4 y la altura de B es 0. El mínimo de estos dos heights es 0. Tomamos el mínimo y le sumamos 1.
El vértice resaltado tiene exceso de flujo y hay un adyacente con menor altura, por lo que ocurre push(). El exceso de flujo del vértice A es 2 y la capacidad del borde (A, B) es 1. Por lo tanto, la cantidad de flujo empujado es 1 (mínimo de dos valores).
El vértice resaltado se vuelve a etiquetar (la altura se convierte en 1) ya que tiene exceso de flujo y no hay ningún adyacente con menor altura.
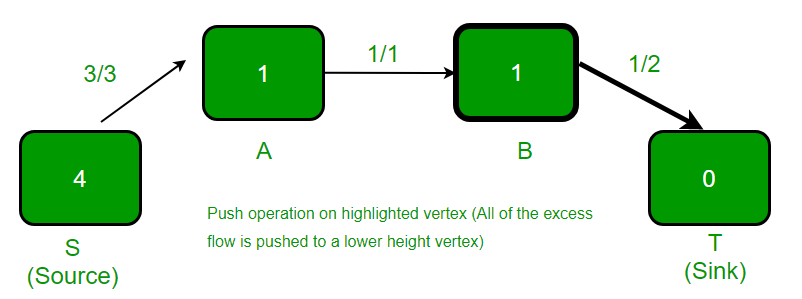
El vértice resaltado tiene un exceso de flujo y hay un adyacente con una altura más baja, por lo que el flujo() se empuja de B a T.
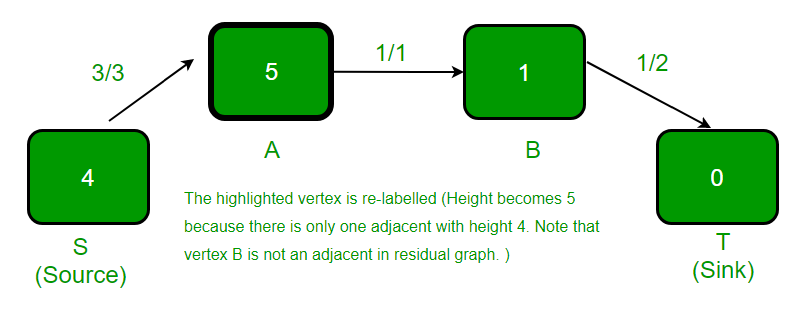
El vértice resaltado se vuelve a etiquetar (la altura se convierte en 5) ya que tiene exceso de flujo y no hay ningún adyacente con menor altura.
El vértice resaltado tiene exceso de flujo y hay un adyacente con menor altura, por lo que ocurre push().
El vértice resaltado se vuelve a etiquetar (la altura aumenta en 1) ya que tiene exceso de flujo y no hay ningún adyacente con menor altura.