Hay 1000 bombillas y 1000 personas. Todas las bombillas están inicialmente apagadas. La persona 1 enciende la bombilla 1, 2, 3, 4, … la persona 2 luego enciende la 2, 4, 6, 8, … la persona 3 luego la 3, 6, 9, … etc. hasta que las 1000 personas hayan hecho esto. ¿Cuál es el estado de las bombillas 25, 93, 576, 132, 605, 26, 45, 37, 36 después de que todas las personas hayan volteado sus respectivas bombillas? ¿Existe una solución general para predecir el estado de una bombilla? ¿Cuántas bombillas quedan encendidas después de que hayan pasado las 1000 personas?
Explicación: Las observaciones clave son:
- La persona 1 enciende la bombilla 1, 2, 3,… que son múltiplos de 1.
- La persona 2 voltea la bombilla 2, 4, 6,… que son múltiplos de 2.
- La persona 3 enciende la bombilla 3, 6, 9,… que son múltiplos de 3.
- De manera similar, la Persona 1000 voltea la bombilla 1000, que es un múltiplo de 1000.
- De las observaciones anteriores, podemos decir que la persona i encenderá bombillas que son múltiplos de i,
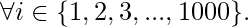
- Por lo tanto, todas las personas para las que j es un múltiplo de su número de persona encenderán una bombilla j. En otras palabras, todas las personas cuyo número de persona i es un factor de j, encenderán la bombilla j,

- Ejemplos:
- (i) La bombilla 10 será volteada por las personas 1, 2, 5, 10 cuyos números personales son factores de 10.
- (ii) La bombilla 12 será volteada por las personas 1, 2, 3, 4, 6, 12 cuyos números de persona son factores de 12.
- (i) La bombilla 10 será volteada por las personas 1, 2, 5, 10 cuyos números personales son factores de 10.
- Por lo tanto, la bombilla 25 será volteada por las personas 1, 5, 25, por lo que será volteada 3 veces, lo cual es extraño y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 25 estará «encendida».
- La bombilla 93 será volteada por las personas 1, 3, 31, 93, por lo que será volteada 4 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 93 estará «apagada».
- La bombilla 576 será volteada por las personas 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576 , por lo que se girará 21 veces, lo cual es extraño y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 576 estará «encendida».
- La bombilla 132 será volteada por las personas 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132, por lo que será volteada 12 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 132 estará «apagada».
- La bombilla 605 será volteada por las personas 1, 5, 11, 55, 121, 605, por lo que será volteada 6 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 605 estará » apagado».
- La bombilla 26 será volteada por las personas 1, 2, 13, 26, por lo que será volteada 4 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 26 estará «apagada».
- La bombilla 45 será volteada por las personas 1, 3, 5, 9, 15, 45, por lo que será volteada 6 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 45 estará » apagado».
- La bombilla 37, que es la bombilla con el número primo, será volteada por las personas 1, 37, por lo que se volteará 2 veces, lo cual es par y dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 37 estará «apagada». ”.
- La bombilla 36 será volteada por las personas 1, 2, 3, 4, 6, 9, 12, 18, 36, por lo que será volteada 9 veces, lo cual es impar y, dado que inicialmente todas las bombillas estaban «apagadas», ahora la bombilla 36 estará “encendida”.
Para averiguar el estado de una bombilla dada:
contamos el número de factores del número de bombilla, y según las observaciones anteriores, si el número de factores es impar, entonces la bombilla estará «encendida», y si es incluso, entonces estará «apagado» al final.
Algoritmo para encontrar cuántas bombillas estarán «encendidas» al final:
contamos los factores de cada número del 1 al 1000. Si la cantidad de factores para cualquier número es impar, la bombilla correspondiente está «encendida», así que actualizamos el resultado, y finalmente, imprimirlo.
A continuación se muestra el código que implementa el algoritmo anterior.
C++
// C++ implementation of above approach
#include <iostream>
using namespace std;
int findOnBulbs(int numberOfBulbs)
{
// initializing the result
int onBulbs = 0;
// to loop over all bulbs from 1 to numberOfBulbs
int bulb = 1;
// to loop over persons to check whether their person number
int person = 1;
// is a factor of light bulb number or not
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
// inner loop to find factors of given bulb
// to count the number of factors of a given bulb
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0) // person is a factor
{
factors++;
// bulb != person*person
if (bulb / person != person)
{
factors++;
}
}
}
// if number of factors is odd, then the
if (factors % 2 == 1)
{
// light bulb will be "on" in the end
cout << "Light bulb "
<< bulb
<< " will be on"
<< "\n";
onBulbs++;
}
}
return onBulbs;
}
// Driver program to test above function
int main()
{
// total number of light bulbs
int numberOfBulbs = 1000;
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
int onBulbs = findOnBulbs(numberOfBulbs);
cout << "Total "
<< onBulbs
<< " light bulbs will be on in the end out of "
<< numberOfBulbs
<< " light bulbs"
<< "\n";
return 0;
}
Java
// Java implementation of the
// above given approach
public class GFG
{
static int findOnBulbs(int numberOfBulbs)
{
// initializing the result
int onBulbs = 0;
// to loop over all bulbs from 1 to numberOfBulbs
int bulb = 1;
// to loop over persons to check whether their person number
int person = 1;
// is a factor of light bulb number or not
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
// inner loop to find factors of given bulb
// to count the number of factors of a given bulb
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0) // person is a factor
{
factors++;
// bulb != person*person
if (bulb / person != person)
{
factors++;
}
}
}
// if number of factors is odd, then the
if (factors % 2 == 1)
{
// light bulb will be "on" in the end
System.out.println("Light bulb " + bulb + " will be on");
onBulbs++;
}
}
return onBulbs;
}
// Driver program to test above function
public static void main(String [] args)
{
// total number of light bulbs
int numberOfBulbs = 1000;
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
int onBulbs = findOnBulbs(numberOfBulbs);
System.out.println("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
// This code is contributed
// by Ryuga
}
Python3
# Python3 code implementing the
# given approach
def findOnBulbs(numberOfBulbs):
# initializing the result
onBulbs = 0
# to loop over all bulbs from
# 1 to numberOfBulbs
bulb = 1
# to loop over persons to check
# whether their person number
person = 1
# Is a factor of light bulb number or not
for bulb in range(1, numberOfBulbs + 1):
# inner loop to find factors of
# given bulb to count the number
# of factors of a given bulb
factors = 0
for person in range(1, int(numberOfBulbs**(0.5)) + 1):
if bulb % person == 0: # person is a factor
factors += 1
# bulb != person*person
if bulb // person != person:
factors += 1
# if number of factors is odd, then the
if factors % 2 == 1:
# light bulb will be "on" in the end
print("Light bulb", bulb, "will be on")
onBulbs += 1
return onBulbs
# Driver Code
if __name__ == "__main__":
# total number of light bulbs
numberOfBulbs = 1000
# to find number of on bulbs in
# the end after all persons have
# flipped the light bulbs
onBulbs = findOnBulbs(numberOfBulbs)
print("Total", onBulbs, "light bulbs will",
"be on in the end out of",
numberOfBulbs, "light bulbs")
# This code is contributed
# by Rituraj Jain
C#
// C# implementation of above approach
using System;
class GFG
{
static int findOnBulbs(int numberOfBulbs)
{
// initializing the result
int onBulbs = 0;
// to loop over all bulbs from 1 to numberOfBulbs
int bulb = 1;
// to loop over persons to check whether their person number
int person = 1;
// is a factor of light bulb number or not
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
// inner loop to find factors of given bulb
// to count the number of factors of a given bulb
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0) // person is a factor
{
factors++;
// bulb != person*person
if (bulb / person != person)
{
factors++;
}
}
}
// if number of factors is odd, then the
if (factors % 2 == 1)
{
// light bulb will be "on" in the end
Console.WriteLine("Light bulb " + bulb + " will be on");
onBulbs++;
}
}
return onBulbs;
}
// Driver program to test above function
public static void Main()
{
// total number of light bulbs
int numberOfBulbs = 1000;
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
int onBulbs = findOnBulbs(numberOfBulbs);
Console.WriteLine("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
// This code is contributed
// by Akanksha Rai
PHP
<?php
// PHP implementation of above approach
function findOnBulbs($numberOfBulbs)
{
// initializing the result
$onBulbs = 0;
// to loop over all bulbs from
// 1 to numberOfBulbs
$bulb = 1;
// to loop over persons to check
// whether their person number
$person = 1;
// is a factor of light bulb number or not
for ($bulb = 1;
$bulb <= $numberOfBulbs; $bulb++)
{
// inner loop to find factors of given
// bulb to count the number of factors
// of a given bulb
$factors = 0;
for ($person = 1;
$person * $person <= $numberOfBulbs; $person++)
{
if ($bulb % $person == 0) // person is a factor
{
$factors++;
// bulb != person*person
if ($bulb / $person != $person)
{
$factors++;
}
}
}
// if number of factors is odd, then the
if ($factors % 2 == 1)
{
// light bulb will be "on" in the end
echo "Light bulb " . $bulb .
" will be on" ."\n";
$onBulbs++;
}
}
return $onBulbs;
}
// Driver Code
// total number of light bulbs
$numberOfBulbs = 1000;
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
$onBulbs = findOnBulbs($numberOfBulbs);
echo "Total " . $onBulbs . " light bulbs will " .
"be on in the end out of " . $numberOfBulbs .
" light bulbs" ."\n";
// This code is contributed by ita_c
?>
Javascript
<script>
// Javascript implementation of the
// above given approach
function findOnBulbs(numberOfBulbs)
{
// initializing the result
let onBulbs = 0;
// to loop over all bulbs from 1 to numberOfBulbs
let bulb = 1;
// to loop over persons to check whether their person number
let person = 1;
// is a factor of light bulb number or not
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
// inner loop to find factors of given bulb
// to count the number of factors of a given bulb
let factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0) // person is a factor
{
factors++;
// bulb != person*person
if (bulb / person != person)
{
factors++;
}
}
}
// if number of factors is odd, then the
if (factors % 2 == 1)
{
// light bulb will be "on" in the end
document.write("Light bulb " + bulb + " will be on<br>");
onBulbs++;
}
}
return onBulbs;
}
// Driver program to test above function
// total number of light bulbs
let numberOfBulbs = 1000;
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
let onBulbs = findOnBulbs(numberOfBulbs);
document.write("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
// This code is contributed by avanitrachhadiya2155
</script>
El programa anterior está escrito en O(n*sqrt(n)).
A partir de la observación, está claro que siempre que el número de factores sea impar, la bombilla estará encendida.
Para cualquier número no cuadrado con cada divisor, existe un cociente correspondiente, por lo que el número de factores será par.
Para todo número cuadrado, cuando lo dividimos por su raíz cuadrada, el cociente será el mismo número, es decir, su raíz cuadrada. Por lo tanto, tiene un número impar de factores.
Por lo tanto, podemos escribir un código eficiente para este problema que se calcula en O(sqrt(n)).
C++
#include<iostream>
#include<math.h>
using namespace std;
int main()
{
int numberOfBulbs = 1000;
int root = sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
cout << "Light bulb " << (i * i)
<< " will be on" << endl;
}
cout << "Total " << root
<< " light bulbs will be on in the end out of "
<< numberOfBulbs << " light bulbs" << endl;
return 0;
}
// This code is contributed by Apurvaraj
Java
import java.io.*;
class GFG {
// Driver code
public static void main (String[] args) {
int numberOfBulbs = 1000;
int root = (int) Math.sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
System.out.println("Light bulb " + (i * i) +" will be on");
}
System.out.println("Total " + root
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
// This code is contributed b ab2127.
Python3
import math
root = int(math.sqrt(1000))
for i in range(1, root + 1):
print("Light bulb %d will be on"%(i * i))
print("""Total %d light bulbs will be on
in the end out of 1000 light bulbs"""%root)
C#
using System;
using System.Collections.Generic;
class GFG
{
// Driver code
public static void Main(String [] args)
{
int numberOfBulbs = 1000;
int root = (int) Math.Sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
Console.WriteLine("Light bulb " + (i * i) +" will be on");
}
Console.WriteLine("Total " + root
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
var numberOfBulbs = 1000;
var root = parseInt( Math.sqrt(numberOfBulbs));
for (i = 1; i < root + 1; i++) {
document.write("Light bulb " + (i * i) + " will be on<br/>");
}
document.write(
"Total " + root + " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs<br/>");
// This code is contributed by Rajput-Ji
</script>
Producción:
Light bulb 1 will be on Light bulb 4 will be on Light bulb 9 will be on Light bulb 16 will be on Light bulb 25 will be on Light bulb 36 will be on Light bulb 49 will be on Light bulb 64 will be on Light bulb 81 will be on Light bulb 100 will be on Light bulb 121 will be on Light bulb 144 will be on Light bulb 169 will be on Light bulb 196 will be on Light bulb 225 will be on Light bulb 256 will be on Light bulb 289 will be on Light bulb 324 will be on Light bulb 361 will be on Light bulb 400 will be on Light bulb 441 will be on Light bulb 484 will be on Light bulb 529 will be on Light bulb 576 will be on Light bulb 625 will be on Light bulb 676 will be on Light bulb 729 will be on Light bulb 784 will be on Light bulb 841 will be on Light bulb 900 will be on Light bulb 961 will be on Total 31 light bulbs will be on in the end out of 1000 light bulbs