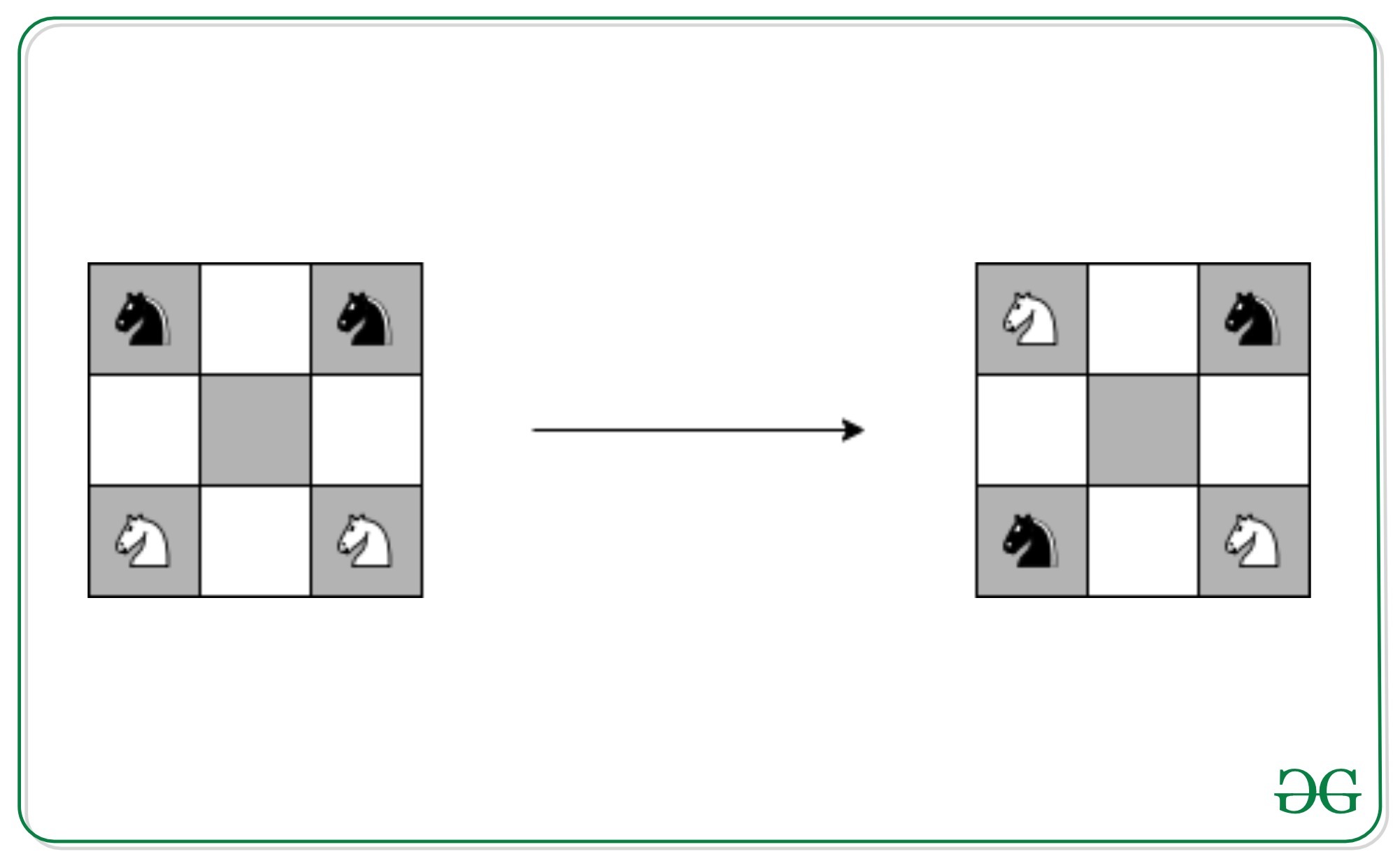
Hay cuatro caballos en un tablero de ajedrez de 3 x 3 . Los dos caballos blancos están en las dos esquinas inferiores y los dos caballos negros están en las dos esquinas superiores del tablero. Encuentre la secuencia más corta de movimientos para lograr la posición final como se muestra en la figura o demuestre que tal secuencia no existe.
Solución:
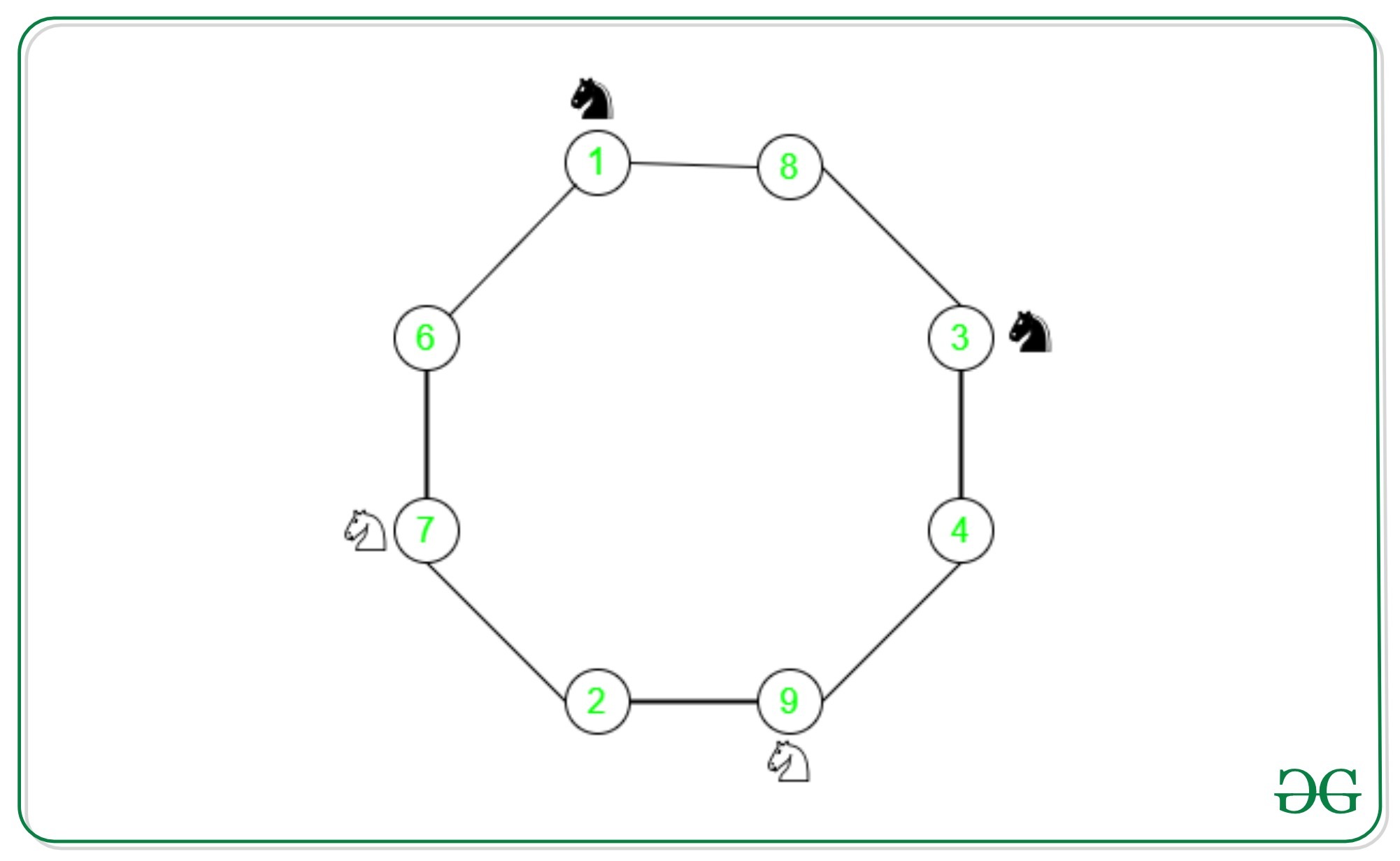
Un caballo en un juego de ajedrez tiene movimientos en forma de L. Por lo tanto, puede ocupar como máximo dos posiciones diferentes en un solo movimiento en un tablero de 3 x 3 . Considere un gráfico donde los vértices representan el número de celda y los bordes entre ellos representan los movimientos que pueden hacer varios caballos.
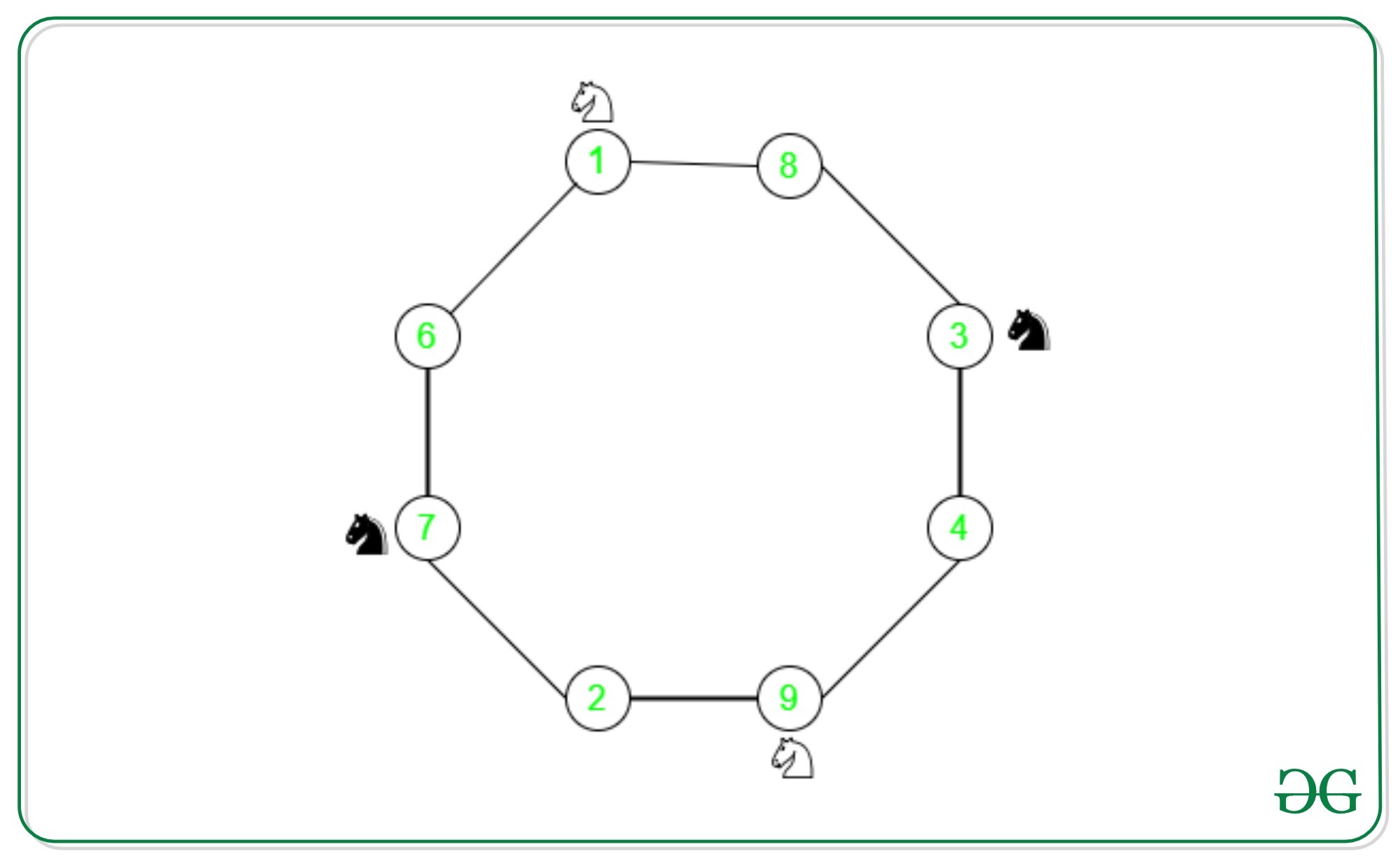
En este gráfico tenemos dos caballos de color negro, seguidos de dos caballos de color blanco. Consideremos que el caballo de la celda 1 se mueve a la celda 6. Ahora, para moverse a su posición final, la celda 7, el caballo de la celda 7 debe moverse a la celda 2. Sin embargo, su posición final es la celda 1, como se muestra. Entonces la configuración solicitada es imposible de lograr. Esto es cierto para cualquier secuencia de movimientos, ya sea en el sentido de las agujas del reloj o en el sentido contrario, ya que el orden de los caballos sigue siendo el mismo . Sin embargo, la configuración final en cuestión exige una secuencia alterna de colores de los caballeros. Entonces, este rompecabezas no tiene solución .
Publicación traducida automáticamente
Artículo escrito por CharchitKapoor y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA