Sahil y Ritik son hermanos. Un día estaban discutiendo quién es más inteligente. Pero poco a poco la discusión se convirtió en una discusión. La madre vino y trató de manejar la situación. Ella les dio un problema para resolver y el que resolverá el problema primero, será considerado más inteligente que el otro. El problema es:
en un grupo de 6 personas, es posible que encuentre que algunas personas son amigos en Facebook, o puede encontrar que nadie es amigo en Facebook. Se supone que los hermanos deben demostrar que siempre hay un grupo de 3 personas donde:
– Las 3 personas son amigos mutuos en Facebook.
– Las 3 personas son extraños (es decir, nadie es amigo en Facebook).
¿Puedes ayudar a los hermanos a llegar a la solución?
Respuesta:
El problema se puede visualizar utilizando la teoría de grafos. Imagina que cada persona es el vértice de un gráfico. Representa a 6 personas usando 6 vértices de la gráfica. Dibuja una línea azul entre las personas que son amigos y una línea roja entre las personas que no son amigos.

Vértices que representan personas..
Desde un vértice, puede haber 0,1,2,3,4,5 líneas azules que van acompañadas de 5,4,3,2,1,0 líneas rojas. Desde un vértice, dibuja líneas a otros vértices. Las líneas que no sean azules deben ser rojas y viceversa. El número de líneas rojas y líneas azules siempre será 5. Por ejemplo, si hay 2 líneas rojas, entonces debe haber 3 líneas azules. Debido a esto, siempre habrá 3+ líneas azules o 3+ líneas rojas (es decir, cualquiera estará presente al menos 3 veces). Considere ambos casos por separado.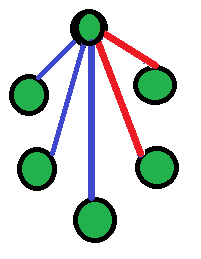
Primero considere que hay 3 líneas rojas y 2 líneas azules. La representación se muestra en la figura como: 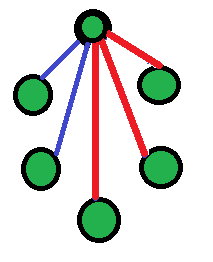
Mira los vértices que están conectados por líneas rojas. Mira a los amigos de esta persona. Si ninguno es amigo, significa que son 3 extraños en común (se muestra con un triángulo rojo).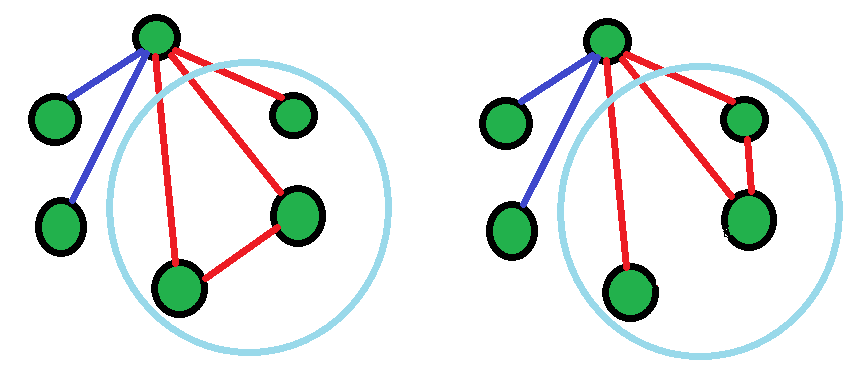
Si alguno es amigo, significa que son 3 amigos mutuos (mostrados por un triángulo azul).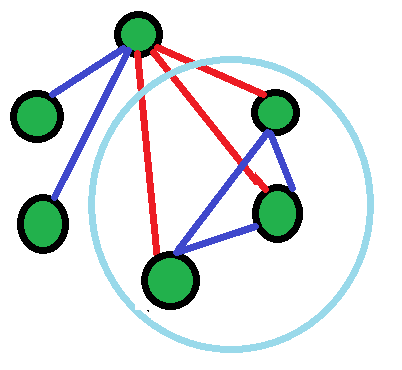
Entonces, esto prueba que siempre hay al menos 3 amigos en común o al menos 3 extraños.
Lo mismo se puede probar tomando el otro caso (es decir, si tenemos 3 líneas azules y 2 líneas rojas). En ese caso, habría un triángulo azul si hay al menos 3 amigos y un triángulo rojo si hay al menos 3 extraños.
Referencias- Youtube-El acertijo de la amistad
Publicación traducida automáticamente
Artículo escrito por Sahil_Bansall y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA