Rompecabezas | Dragones paradójicos

Rompecabezas : Hay 3 dragones. Uno de ellos siempre dice la verdad, uno siempre miente y uno alterna entre la verdad y la mentira. Una serie de conversaciones entre Ram y los 3 dragones te permite identificar la naturaleza de cada dragón.

• Dragón 1: «Puedes hacernos una pregunta, luego debes adivinar qué dragón es cuál».
• Dragón 2: “Está mintiendo. Puede recibir tres preguntas”
• Dragón 3: “Oh no. Definitivamente es una pregunta”
• Ram: «¿Qué diría el segundo dragón si le preguntara si el tercer dragón había estado mintiendo cuando estuvo de acuerdo con el primero en que solo podía hacer una pregunta?»
• Dragón 1: Diría: «Sí, el tercer dragón estaba mintiendo»
• Entonces Ram hizo una segunda pregunta dirigida a los tres dragones, pero permanecieron en silencio. El rompecabezas fue resuelto, explique.

Solución : Basado en el silencio después de que Ram hizo la segunda pregunta, se puede inferir que hacer una pregunta era cierto como lo dijo el Dragón 1. Entonces, el Dragón 1 y el Dragón 3 están diciendo la verdad por primera vez. Esto plantea dos casos:

dragones	Caso 1	Caso 2
Dragón 1	siempre habla la verdad	columna3
Dragón 2	siempre miente	siempre miente
Dragón 3	siempre habla la verdad	suplentes

Ahora analicemos cada caso.
Caso 1: Si este caso es cierto, la declaración del Dragón 1 «El Dragón 2 dirá que el Dragón 3 está mintiendo» habría sido una mentira. Si el Dragón 1 miente, entonces la declaración del Dragón 2 sería «El Dragón 3 está diciendo la verdad», pero según el Caso 1, el Dragón 2 siempre miente y el Dragón 3 siempre dice la verdad. Estas declaraciones se contradicen con el caso de Dragon 3 siempre diciendo la verdad.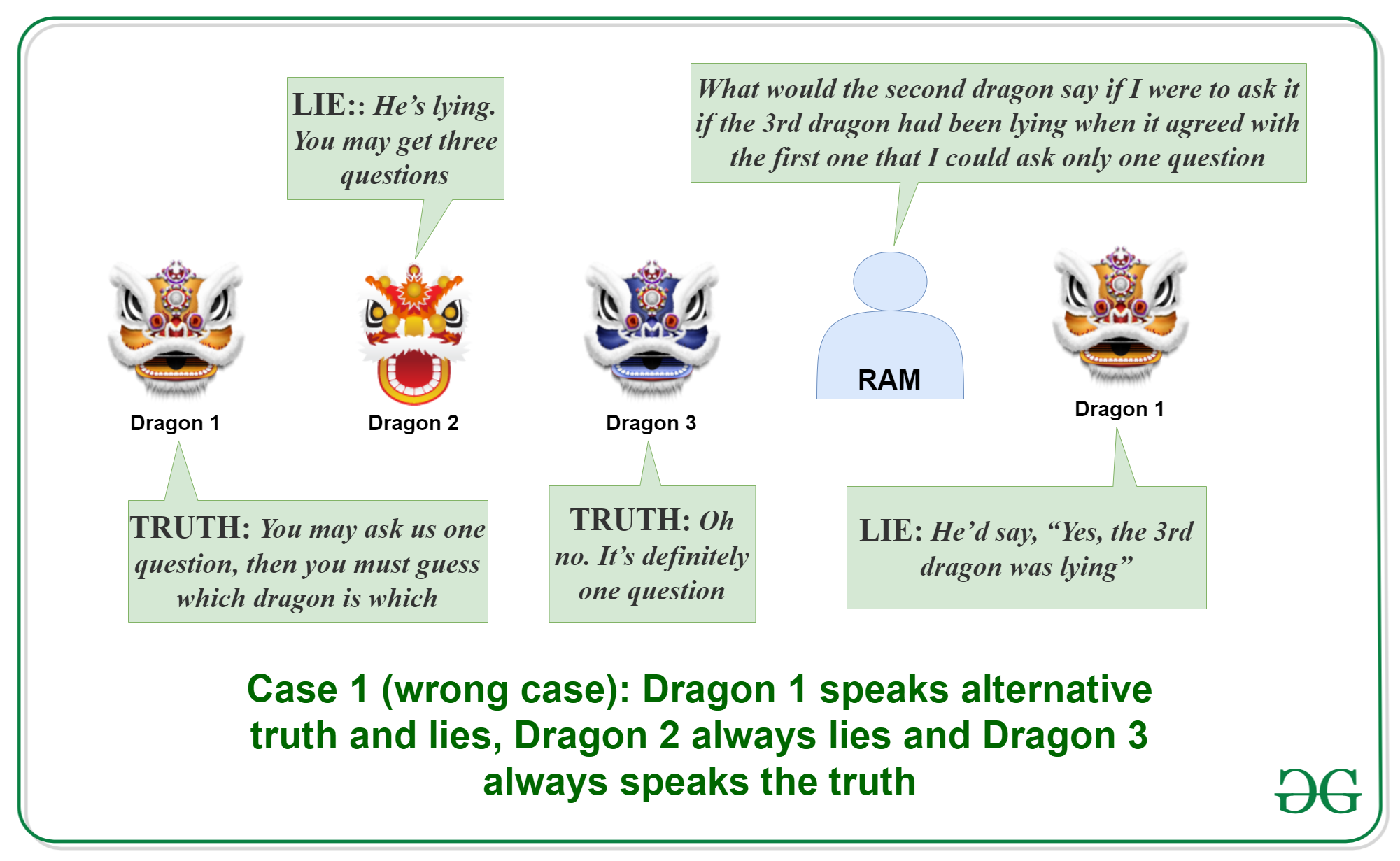

Caso 2: Si este caso es Verdadero, la declaración del Dragón 1 «El Dragón 2 dirá que el Dragón 3 está mintiendo» sería verdadera. Entonces, la declaración de Dragon 2 sería «Dragon 3 está mintiendo», lo cual sería una mentira. Por lo tanto, el Caso 2 es correcto.