Hay un granjero que desea cruzar un río pero no está solo. También tiene una cabra, un lobo y un repollo junto con él. Solo hay un bote disponible que puede sostener al granjero y a la cabra, el lobo o el repollo. Entonces, a la vez, el bote puede tener solo dos objetos (granjero y otro).
Pero el problema es que si la cabra y el lobo se quedan solos (ya sea en el bote o en tierra), el lobo se comerá a la cabra. De manera similar, si la cabra y el repollo se dejan solos, entonces la cabra se comerá el repollo. El granjero quiere cruzar el río con sus tres pertenencias: cabra, lobo y repollo.
¿Qué estrategia debería usar para hacerlo?
Solución 1: Llevar al lobo al otro lado dejará la cabra y el repollo juntos. También quitar el repollo hará que el lobo y la cabra estén solos. Por lo tanto, el granjero primero tomará la cabra del otro lado y regresará solo. Tenemos granjero, lobo y repollo en un lado y cabra en el otro lado.
Ahora, se llevará al lobo, dejará al lobo en el otro lado y regresará con la cabra. Así que ahora, de un lado, tenemos granjero, repollo y cabra, y del otro lado, tenemos un lobo.
Ahora, se lleva el repollo y regresa solo. Así que ahora el escenario es: granjero, cabra por un lado y lobo, repollo por el otro lado.
Ahora, finalmente, cruza el río con la cabra y logra llevarse todas sus pertenencias.
Solución 2: Este problema se puede resolver usando la teoría de grafos.
Considere 2 estados: inicial (A) y final (B).
Inicialmente, el lado derecho del río no tiene nada y la cabra, el repollo y el lobo están a la izquierda. Y en el estado final, los tres (cabra, repollo y lobo) estarán en el lado derecho. ¿Cómo podemos llegar al estado B desde el estado A? La orilla derecha puede tener estas combinaciones de cabra (G), repollo (C), lobo (W).
-> 0, G, W, C, GW , GC , WC, GWC
0 representa el estado inicial (A) y GWC representa el estado final (B). Podemos modelar este problema como un gráfico ponderado no dirigido. Donde cada borde en el gráfico tiene peso 1 o infinito.
Este gráfico se puede utilizar para representar nuestro problema.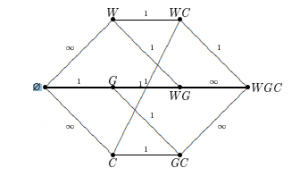
Ahora, todos los caminos que tienen un peso infinito no se pueden recorrer, de lo contrario se violarán las restricciones del problema. Entonces, tenemos que movernos de A a B usando rutas que tienen un peso de 1, y podemos encontrar una ruta válida usando el algoritmo de ruta más corta de Dijkstra.
Explicación:
Está muy claro que inicialmente, el barquero solo puede llevarse la cabra con él. Entonces, del vértice 0 al vértice G, establecemos el peso en 1. En otros casos, (0 a W, 0 a C) alguien será devorado. Por lo tanto, establecemos estos pesos en infinito.
Usando una intuición similar, es fácil idear la solución.
Este artículo es una contribución de Arushi Dhamija. . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA