Tienes un aro de baloncesto y alguien dice que puedes jugar uno de dos juegos.
Juego 1: Tienes una oportunidad para hacer el aro.
Juego 2: obtienes tres tiros y tienes que hacer dos de tres tiros.
Si p es la probabilidad de hacer un tiro en particular, ¿para qué valores de p debería elegir un juego u otro?
Responder:
Probabilidad de ganar el Juego 1:
La probabilidad de ganar el juego 1 es p, por definición.
Probabilidad de ganar el Juego 2:
Sea s(k, n) la probabilidad de hacer exactamente k tiros de n. La probabilidad de ganar el Juego 2 es la probabilidad de hacer exactamente dos tiros de tres O hacer los tres tiros. En otras palabras:
P(ganador) = s(2, 3) + s(3, 3)
La probabilidad de hacer los tres tiros es:
s(3, 3) =
La probabilidad de acertar exactamente dos tiros es:
P(acertar 1 y 2, y fallar 3) + P(acertar 1 y 3, y fallar 2) + P(acertar 2 y 3, y fallar 1)
= [p * p * (1-p)] + [p * (1-p) * p] + [(1-p) * p * p] = 3*(1-p)*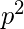
Sumando estos juntos, obtenemos:
=+ 3(1-p)
=
+ 3
- 3
= 3
- 2
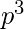
¿Qué juego deberías jugar?
Deberías jugar el Juego 1 si P (Juego 1) > P (Juego 2):
p > 3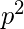 - 2
- 2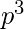 1 > 3p - 2
1 > 3p - 2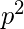 2
2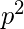 - 3p + 1 > 0
(2p - 1)(p - 1) > 0
- 3p + 1 > 0
(2p - 1)(p - 1) > 0
Ambos términos deben ser positivos, o ambos deben ser negativos, pero sabemos que p < 1, entonces p – 1 < 0. Esto significa que ambos términos deben ser negativos.
2p - 1 < 0
2p < 1
p < 0.5
Entonces, deberíamos jugar el Juego 1 si 0 < p < 0.5 y el Juego 2 si 0.5 < p < 1.
Si p = 0, 0.5 o 1 entonces P(Juego 1) = P(Juego 2), entonces no importa qué juego juguemos.
Este artículo es una contribución de Brahmani Sai . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA