El cambio de tamaño de la imagen es un concepto crucial que desea aumentar o reducir la cantidad de píxeles en una imagen. Las aplicaciones de cambio de tamaño de imagen pueden ocurrir en una forma más amplia de escenarios: transliteración de la imagen, corrección de la distorsión de la lente, cambio de perspectiva y rotación de una imagen. Los resultados del cambio de tamaño varían mucho según el tipo de algoritmo de interpolación utilizado.
Nota: Al aplicar algoritmos de interpolación, es seguro que se perderá parte de la información, ya que se trata de algoritmos de aproximación.
¿Qué es la interpolación?
La interpolación funciona mediante el uso de datos conocidos para estimar valores en puntos desconocidos. Por ejemplo: si desea comprender la intensidad de píxeles de una imagen en una ubicación seleccionada dentro de la cuadrícula (digamos coordenada (x, y), pero solo (x-1, y-1) y (x+1,y+1 ) son conocidos, estimará el valor en (x, y) mediante interpolación lineal. Cuanto mayor sea la cantidad de valores ya conocidos, mayor será la precisión del valor de píxel estimado.
Algoritmos de interpolación
Los diferentes algoritmos de interpolación incluyen el vecino más cercano, bilineal , bicúbico y otros. Apostando por su complejidad, estos utilizan entre 0 y 256 (o más) píxeles adyacentes al interpolar. La precisión de esos algoritmos aumenta significativamente al aumentar el número de píxeles vecinos considerados durante la evaluación del nuevo valor de píxel. Los algoritmos de interpolación se utilizan predominantemente para cambiar el tamaño y distorsionar una imagen de alta resolución a una imagen de resolución ocasional. Hay varios algoritmos de interpolación, uno de ellos es la interpolación bicúbica.
Interpolación bicúbica
Además de ir a la vecindad 2×2 de valores de píxeles conocidos, Bicubic va un paso más allá de la bilinealidad al considerar la vecindad 4×4 más cercana de píxeles conocidos, para un total de 16 píxeles. Los píxeles que están más cerca del que se va a estimar reciben pesos más altos en comparación con los que están más lejos. Por lo tanto, los píxeles más lejanos tienen la menor cantidad de peso. Los resultados de la interpolación bicúbica son mucho mejores en comparación con los algoritmos NN o bilineales. Esto puede deberse a que se considera una mayor cantidad de valores de píxeles conocidos al estimar el valor deseado. Por lo tanto, es uno de los principales métodos de interpolación estándar.
Implementando la interpolación bicúbica con Python
Importación de los módulos necesarios: importamos todas las dependencias como cv2 (OpenCV), NumPy y matemáticas.
Python
# Import modules import cv2 import numpy as np import math import sys, time
Escritura de la función del núcleo de interpolación para la interpolación bicúbica: El núcleo de interpolación para la interpolación bicúbica tiene la forma:
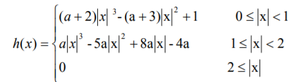
Ecuación del núcleo
Aquí, el valor del coeficiente a determina el rendimiento del núcleo y se encuentra principalmente entre -0,5 y -0,75 para un rendimiento óptimo.
Python
# Interpolation kernel def u(s, a): if (abs(s) >= 0) & (abs(s) <= 1): return (a+2)*(abs(s)**3)-(a+3)*(abs(s)**2)+1 elif (abs(s) > 1) & (abs(s) <= 2): return a*(abs(s)**3)-(5*a)*(abs(s)**2)+(8*a)*abs(s)-4*a return 0
Agregar relleno a la imagen de entrada: defina la función de relleno para agregar bordes a su imagen. OpenCV tiene varias funciones de relleno. Cuando las interpolaciones requieren rellenar el origen, el límite de la imagen de origen debe extenderse porque necesita tener información que le permita calcular los valores de píxel de todos los píxeles de destino que se encuentran a lo largo de los límites.
Python
# Padding def padding(img, H, W, C): zimg = np.zeros((H+4, W+4, C)) zimg[2:H+2, 2:W+2, :C] = img # Pad the first/last two col and row zimg[2:H+2, 0:2, :C] = img[:, 0:1, :C] zimg[H+2:H+4, 2:W+2, :] = img[H-1:H, :, :] zimg[2:H+2, W+2:W+4, :] = img[:, W-1:W, :] zimg[0:2, 2:W+2, :C] = img[0:1, :, :C] # Pad the missing eight points zimg[0:2, 0:2, :C] = img[0, 0, :C] zimg[H+2:H+4, 0:2, :C] = img[H-1, 0, :C] zimg[H+2:H+4, W+2:W+4, :C] = img[H-1, W-1, :C] zimg[0:2, W+2:W+4, :C] = img[0, W-1, :C] return zimg
Escribiendo la función de interpolación bicúbica: Defina la función bicúbica y pase la imagen como entrada. (Puede variar el factor de escala como x2 o x4 según el requisito).
Python
# Bicubic operation
def bicubic(img, ratio, a):
# Get image size
H, W, C = img.shape
# Here H = Height, W = weight,
# C = Number of channels if the
# image is coloured.
img = padding(img, H, W, C)
# Create new image
dH = math.floor(H*ratio)
dW = math.floor(W*ratio)
# Converting into matrix
dst = np.zeros((dH, dW, 3))
# np.zeroes generates a matrix
# consisting only of zeroes
# Here we initialize our answer
# (dst) as zero
h = 1/ratio
print('Start bicubic interpolation')
print('It will take a little while...')
inc = 0
for c in range(C):
for j in range(dH):
for i in range(dW):
# Getting the coordinates of the
# nearby values
x, y = i * h + 2, j * h + 2
x1 = 1 + x - math.floor(x)
x2 = x - math.floor(x)
x3 = math.floor(x) + 1 - x
x4 = math.floor(x) + 2 - x
y1 = 1 + y - math.floor(y)
y2 = y - math.floor(y)
y3 = math.floor(y) + 1 - y
y4 = math.floor(y) + 2 - y
# Considering all nearby 16 values
mat_l = np.matrix([[u(x1, a), u(x2, a), u(x3, a), u(x4, a)]])
mat_m = np.matrix([[img[int(y-y1), int(x-x1), c],
img[int(y-y2), int(x-x1), c],
img[int(y+y3), int(x-x1), c],
img[int(y+y4), int(x-x1), c]],
[img[int(y-y1), int(x-x2), c],
img[int(y-y2), int(x-x2), c],
img[int(y+y3), int(x-x2), c],
img[int(y+y4), int(x-x2), c]],
[img[int(y-y1), int(x+x3), c],
img[int(y-y2), int(x+x3), c],
img[int(y+y3), int(x+x3), c],
img[int(y+y4), int(x+x3), c]],
[img[int(y-y1), int(x+x4), c],
img[int(y-y2), int(x+x4), c],
img[int(y+y3), int(x+x4), c],
img[int(y+y4), int(x+x4), c]]])
mat_r = np.matrix(
[[u(y1, a)], [u(y2, a)], [u(y3, a)], [u(y4, a)]])
# Here the dot function is used to get the dot
# product of 2 matrices
dst[j, i, c] = np.dot(np.dot(mat_l, mat_m), mat_r)
# If there is an error message, it
# directly goes to stderr
sys.stderr.write('\n')
# Flushing the buffer
sys.stderr.flush()
return dst
Tomando la entrada del usuario y pasando la entrada a la función bicúbica para generar la imagen redimensionada: Pasando la imagen deseada a la función bicúbica y guardando la salida como un archivo separado en el directorio.
Python3
# Read image
# You can put your input image over here
# to run bicubic interpolation
# The read function of Open CV is used
# for this task
img = cv2.imread('gfg.png')
# Scale factor
ratio = 2
# Coefficient
a = -1/2
# Passing the input image in the
# bicubic function
dst = bicubic(img, ratio, a)
print('Completed!')
# Saving the output image
cv2.imwrite('bicubic.png', dst)
bicubicImg=cv2.imread('bicubic.png')
Compare la imagen generada con la imagen de entrada: use el método shape() para comparar la altura, el ancho y el modo de color de ambas imágenes.
Python3
# display shapes of both images
print('Original Image Shape:',img.shape)
print('Generated Bicubic Image Shape:',bicubicImg.shape)
Código completo:
Imagen de entrada:

gfg.png
Python3
# import modules
import cv2
import numpy as np
import math
import sys
import time
# Interpolation kernel
def u(s, a):
if (abs(s) >= 0) & (abs(s) <= 1):
return (a+2)*(abs(s)**3)-(a+3)*(abs(s)**2)+1
elif (abs(s) > 1) & (abs(s) <= 2):
return a*(abs(s)**3)-(5*a)*(abs(s)**2)+(8*a)*abs(s)-4*a
return 0
# Padding
def padding(img, H, W, C):
zimg = np.zeros((H+4, W+4, C))
zimg[2:H+2, 2:W+2, :C] = img
# Pad the first/last two col and row
zimg[2:H+2, 0:2, :C] = img[:, 0:1, :C]
zimg[H+2:H+4, 2:W+2, :] = img[H-1:H, :, :]
zimg[2:H+2, W+2:W+4, :] = img[:, W-1:W, :]
zimg[0:2, 2:W+2, :C] = img[0:1, :, :C]
# Pad the missing eight points
zimg[0:2, 0:2, :C] = img[0, 0, :C]
zimg[H+2:H+4, 0:2, :C] = img[H-1, 0, :C]
zimg[H+2:H+4, W+2:W+4, :C] = img[H-1, W-1, :C]
zimg[0:2, W+2:W+4, :C] = img[0, W-1, :C]
return zimg
# Bicubic operation
def bicubic(img, ratio, a):
# Get image size
H, W, C = img.shape
# Here H = Height, W = weight,
# C = Number of channels if the
# image is coloured.
img = padding(img, H, W, C)
# Create new image
dH = math.floor(H*ratio)
dW = math.floor(W*ratio)
# Converting into matrix
dst = np.zeros((dH, dW, 3))
# np.zeroes generates a matrix
# consisting only of zeroes
# Here we initialize our answer
# (dst) as zero
h = 1/ratio
print('Start bicubic interpolation')
print('It will take a little while...')
inc = 0
for c in range(C):
for j in range(dH):
for i in range(dW):
# Getting the coordinates of the
# nearby values
x, y = i * h + 2, j * h + 2
x1 = 1 + x - math.floor(x)
x2 = x - math.floor(x)
x3 = math.floor(x) + 1 - x
x4 = math.floor(x) + 2 - x
y1 = 1 + y - math.floor(y)
y2 = y - math.floor(y)
y3 = math.floor(y) + 1 - y
y4 = math.floor(y) + 2 - y
# Considering all nearby 16 values
mat_l = np.matrix([[u(x1, a), u(x2, a), u(x3, a), u(x4, a)]])
mat_m = np.matrix([[img[int(y-y1), int(x-x1), c],
img[int(y-y2), int(x-x1), c],
img[int(y+y3), int(x-x1), c],
img[int(y+y4), int(x-x1), c]],
[img[int(y-y1), int(x-x2), c],
img[int(y-y2), int(x-x2), c],
img[int(y+y3), int(x-x2), c],
img[int(y+y4), int(x-x2), c]],
[img[int(y-y1), int(x+x3), c],
img[int(y-y2), int(x+x3), c],
img[int(y+y3), int(x+x3), c],
img[int(y+y4), int(x+x3), c]],
[img[int(y-y1), int(x+x4), c],
img[int(y-y2), int(x+x4), c],
img[int(y+y3), int(x+x4), c],
img[int(y+y4), int(x+x4), c]]])
mat_r = np.matrix(
[[u(y1, a)], [u(y2, a)], [u(y3, a)], [u(y4, a)]])
# Here the dot function is used to get
# the dot product of 2 matrices
dst[j, i, c] = np.dot(np.dot(mat_l, mat_m), mat_r)
# If there is an error message, it
# directly goes to stderr
sys.stderr.write('\n')
# Flushing the buffer
sys.stderr.flush()
return dst
# Read image
# You can put your input image over
# here to run bicubic interpolation
# The read function of Open CV is used
# for this task
img = cv2.imread('gfg.png')
# Scale factor
ratio = 2
# Coefficient
a = -1/2
# Passing the input image in the
# bicubic function
dst = bicubic(img, ratio, a)
print('Completed!')
# Saving the output image
cv2.imwrite('bicubic.png', dst)
bicubicImg = cv2.imread('bicubic.png')
# display shapes of both images
print('Original Image Shape:', img.shape)
print('Generated Bicubic Image Shape:', bicubicImg.shape)
Producción:

Imagen de salida:

bicúbico.png
Explicación:
Por lo tanto, a partir del código anterior, podemos ver que la imagen de entrada se ha redimensionado utilizando la técnica de interpolación bicúbica. La imagen que se muestra a continuación ha sido comprimida por motivos de publicación. Puede ejecutar el código anterior para ver la implementación de aumentar el tamaño de la imagen sin problemas mediante la interpolación bicúbica. Los valores de píxeles desconocidos aquí se llenan considerando los 16 valores conocidos más cercanos.
Publicación traducida automáticamente
Artículo escrito por sanghavipreet2001 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA