En este artículo, estamos tratando de rastrear un objeto en el video con la imagen ya dada. También podemos rastrear el objeto en la imagen. Antes de ver el seguimiento de objetos usando homografía, déjenos saber algunos conceptos básicos.
¿Qué es la Homografía?
La homografía es una transformación que mapea los puntos en un punto al punto correspondiente en otra imagen. La homografía es una array de 3×3:
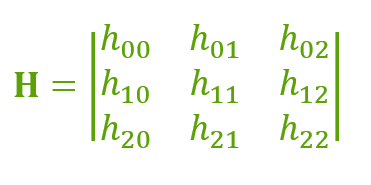
Si 2 puntos no están en el mismo plano entonces tenemos que usar 2 homógrafos. De manera similar, para n planos, tenemos que usar n homógrafos. Si tenemos más homógrafos, debemos manejarlos todos correctamente. Es por eso que usamos la coincidencia de características.
Importación de datos de imagen: Estaremos leyendo la siguiente imagen:

La imagen de arriba es la portada del libro y se almacena como ‘img.jpg’.
Python
# importing the required libraries
import cv2
import numpy as np
# reading image in grayscale
img = cv2.imread("img.jpg", cv2.IMREAD_GRAYSCALE)
# initializing web cam
cap = cv2.VideoCapture(0)
Coincidencia de características: la coincidencia de características significa encontrar las características correspondientes de dos conjuntos de datos similares en función de una distancia de búsqueda. Ahora usaremos el algoritmo de cribado y la coincidencia de características de tipo flann.
Python
# creating the SIFT algorithm sift = cv2.xfeatures2d.SIFT_create() # find the keypoints and descriptors with SIFT kp_image, desc_image =sift.detectAndCompute(img, None) # initializing the dictionary index_params = dict(algorithm = 0, trees = 5) search_params = dict() # by using Flann Matcher flann = cv2.FlannBasedMatcher(index_params, search_params)
Ahora, también tenemos que convertir la captura de video en escala de grises y, al usar el comparador apropiado, tenemos que hacer coincidir los puntos de la imagen con el marco.
Aquí, podemos encontrarnos con excepciones cuando empatamos coincidencias porque infinitamente habrá muchos puntos en ambos planos. Para manejar tales condiciones debemos considerar solo algunos puntos, para obtener algunos puntos precisos podemos variar la barrera de distancia.
Python
# reading the frame _, frame = cap.read() # converting the frame into grayscale grayframe = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) # find the keypoints and descriptors with SIFT kp_grayframe, desc_grayframe = sift.detectAndCompute(grayframe, None) # finding nearest match with KNN algorithm matches= flann.knnMatch(desc_image, desc_grayframe, k=2) # initialize list to keep track of only good points good_points=[] for m, n in matches: #append the points according #to distance of descriptors if(m.distance < 0.6*n.distance): good_points.append(m)

Homografía: Para detectar la homografía del objeto tenemos que obtener la array y usar la función findHomography() para obtener la homografía del objeto.
Python
# maintaining list of index of descriptors # in query descriptors query_pts = np.float32([kp_image[m.queryIdx] .pt for m in good_points]).reshape(-1, 1, 2) # maintaining list of index of descriptors # in train descriptors train_pts = np.float32([kp_grayframe[m.trainIdx] .pt for m in good_points]).reshape(-1, 1, 2) # finding perspective transformation # between two planes matrix, mask = cv2.findHomography(query_pts, train_pts, cv2.RANSAC, 5.0) # ravel function returns # contiguous flattened array matches_mask = mask.ravel().tolist()
Todo está hecho hasta ahora, pero cuando tratamos de cambiar o mover el objeto en otra dirección, la computadora no puede encontrar su homógrafo para lidiar con esto, tenemos que usar la transformación de perspectiva. Por ejemplo, los humanos pueden ver objetos cercanos más grandes que objetos lejanos, aquí la perspectiva está cambiando. Esto se llama transformación de perspectiva.
Python
# initializing height and width of the image h, w = img.shape # saving all points in pts pts = np.float32([[0, 0], [0, h], [w, h], [w, 0]]) .reshape(-1, 1, 2) # applying perspective algorithm dst = cv2.perspectiveTransform(pts, matrix)
Al final, veamos la salida.
Python
# using drawing function for the frame
homography = cv2.polylines(frame, [np.int32(dst)], True, (255, 0, 0), 3)
# showing the final output
# with homography
cv2.imshow("Homography", homography)
Producción :

Publicación traducida automáticamente
Artículo escrito por dadimadhav y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA