Python – Prueba de correlación de Pearson entre dos variables

¿Qué es la prueba de correlación?  
La fuerza de la asociación entre dos variables se conoce como prueba de correlación. 
Por ejemplo, si estamos interesados ​​en saber si existe una relación entre las estaturas de padres e hijos, se puede calcular un coeficiente de correlación para responder a esta pregunta.
Para obtener más información sobre la correlación, consulte esto.
Métodos para análisis de correlación: 
 

• Correlación Paramétrica: Mide una dependencia lineal entre dos variables (x e y) se conoce como prueba de correlación paramétrica porque depende de la distribución de los datos.
• Correlación no paramétrica: Kendall(tau) y Spearman(rho) , que son coeficientes de correlación basados ​​en rangos, se conocen como correlación no paramétrica.

Nota: El método más utilizado es el método de correlación paramétrica.
Fórmula de correlación de Pearson: 
 

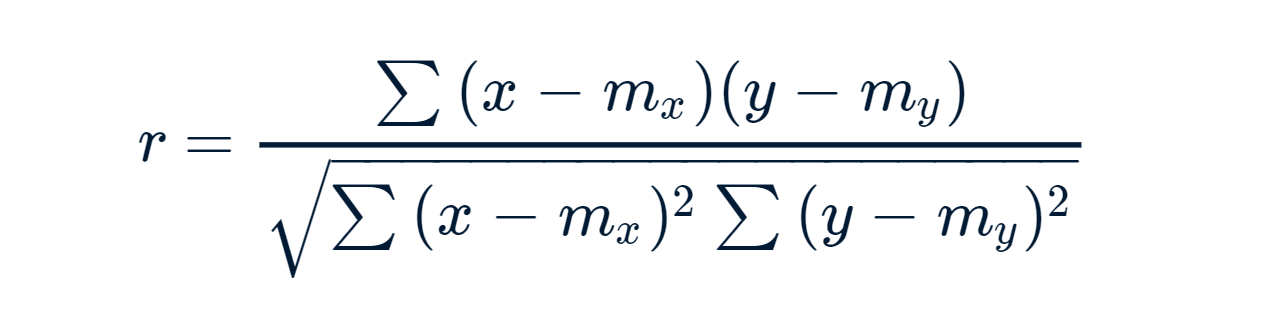
x e y son dos vectores de longitud n 
m, x y m, y corresponde a las medias de x e y, respectivamente.

Nota: 
 

• r toma un valor entre -1 (correlación negativa) y 1 (correlación positiva).
• r = 0 significa que no hay correlación.
• No se puede aplicar a variables ordinales.
• El tamaño de la muestra debe ser moderado (20-30) para una buena estimación.
• Los valores atípicos pueden conducir a valores engañosos, lo que significa que no son robustos con los valores atípicos.

Para calcular la correlación de Pearson en Python, se puede usar la función  pearsonr() .
Funciones de Python 
 

Sintaxis: 
pearsonr(x, y)
Parámetros: 
x, y: Vectores numéricos con la misma longitud 
 

Datos: Descargue el archivo csv aquí.
Código: código de Python para encontrar la correlación de Pearson 
 

# Import those libraries
import pandas as pd
from scipy.stats import pearsonr
 
# Import your data into Python
df = pd.read_csv("Auto.csv")
 
# Convert dataframe into series
list1 = df['weight']
list2 = df['mpg']
 
# Apply the pearsonr()
corr, _ = pearsonr(list1, list2)
print('Pearsons correlation: %.3f' % corr)
 
# This code is contributed by Amiya Rout

Producción: 
 

Pearson correlation is: -0.878

Correlación de Pearson para los datos de 
Anscombe: Los datos de Anscombe, también conocidos como el cuarteto de Anscombe, se componen de cuatro conjuntos de datos que tienen propiedades estadísticas simples casi idénticas, pero que parecen muy diferentes cuando se grafican. Cada conjunto de datos consta de once (x, y) puntos. Fueron construidos en 1973 por el estadístico Francis Anscombe para demostrar tanto la importancia de graficar los datos antes de analizarlos como el efecto de los valores atípicos en las propiedades estadísticas.
Esos 4 conjuntos de 11 puntos de datos se dan aquí. Descargue el archivo csv aquí.  
Cuando trazamos esos puntos se ve así. Estoy considerando 3 conjuntos de 11 puntos de datos aquí. 
 

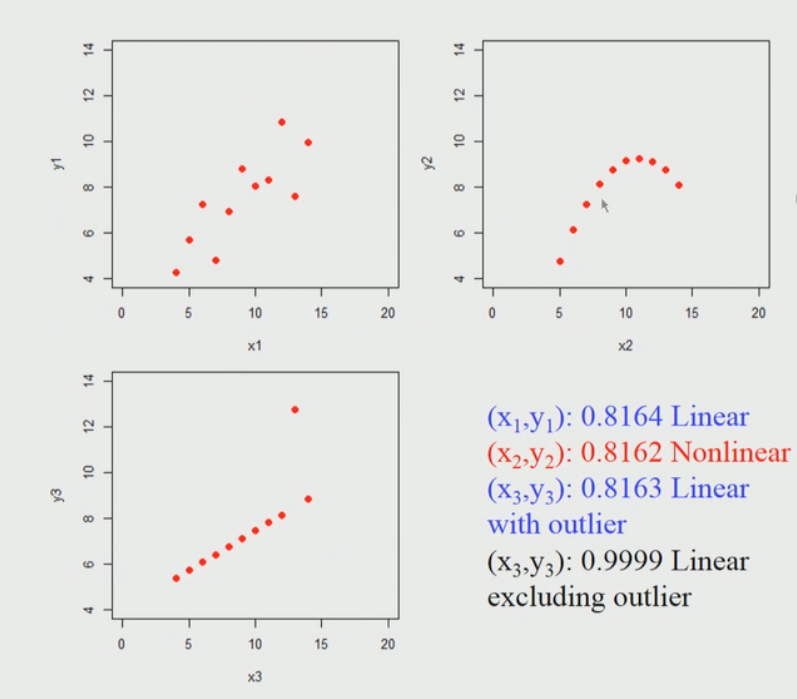
Breve explicación del diagrama anterior: 
Entonces, si aplicamos el coeficiente de correlación de Pearson para cada uno de estos conjuntos de datos, encontramos que es casi idéntico, no importa si realmente lo aplica en un primer conjunto de datos (arriba a la izquierda) o en un segundo conjunto de datos (arriba a la derecha) o el tercer conjunto de datos (abajo a la izquierda). 
Entonces, lo que parece indicar es que si aplicamos la correlación de Pearson y encontramos el coeficiente de correlación alto cercano a uno en este caso del primer conjunto de datos (arriba a la izquierda). El punto clave aquí es que no podemos concluir de inmediato que si el coeficiente de correlación de Pearson va a ser alto, entonces existe una relación lineal entre ellos, por ejemplo, en el segundo conjunto de datos (arriba a la derecha), esta es una relación no lineal y todavía da lugar a un valor alto.