¿Qué es la aceleración? – Barcelona Geeks

Cuando un automóvil parado acelera rápidamente, somos empujados hacia atrás; cuando se usan los frenos, somos empujados hacia adelante contra nuestro asiento; y cuando nuestro automóvil gira rápidamente a la derecha, somos empujados hacia la izquierda. Estamos en estas circunstancias porque nuestro automóvil acelera. Como tal, la aceleración ocurre cada vez que hay un cambio en la velocidad. Veamos algunos ejemplos para ayudarlo a comprender la noción de aceleración.

Suponga que una persona tiene un automóvil que viaja en línea recta a una velocidad constante de 10 km/h mientras observa un helicóptero que vuela a unos 26 km/h. Si alguien te preguntara, ¿dónde ubicas la aceleración en estos dos casos? Su respuesta sin duda será no porque ambos van a la misma velocidad, lo que implica que no existe aceleración en ambos casos.

¿Qué es el movimiento en línea recta?

El movimiento en línea recta se refiere al desplazamiento de un objeto con respecto al tiempo mientras el objeto se mueve a lo largo de una trayectoria recta. Es un movimiento unidimensional y puede expresarse bien usando solo el sistema de coordenadas del eje X. Esto también se denomina movimiento lineal.

Por ejemplo , un automóvil que se mueve a lo largo de la trayectoria lineal en una dirección uniforme.

Los siguientes son los tipos de movimiento en línea recta:

1. Movimiento uniforme: el movimiento unidimensional de un objeto en el que viaja con una velocidad uniforme a lo largo de la trayectoria se denomina movimiento uniforme . Dado que el cuerpo recorre distancias iguales en intervalos de tiempo iguales, la velocidad del cuerpo permanece constante. La velocidad de un objeto permanece igual durante todos los marcos de tiempo, la velocidad promedio del objeto es equivalente a su velocidad real. El objeto no alcanza aceleración en el caso de movimiento uniforme. Por ejemplo, un automóvil que recorre 20 km en la primera hora, 20 km en la hora siguiente, y así sucesivamente durante todo su movimiento.

Ejemplos:

Las manecillas del reloj cubren distancias iguales.
Un automóvil que va a lo largo de una carretera recta y nivelada a una velocidad constante.
Un avión que vuela a una velocidad constante en el aire.

Gráfico de tiempo de distancia para movimiento uniforme

2. Movimiento no uniforme en línea recta (movimiento acelerado): el movimiento unidimensional de un objeto en el que viaja con una velocidad variable a lo largo de la trayectoria se denomina movimiento no uniforme. Como el cuerpo recorre distancias desiguales en intervalos iguales de tiempo, la velocidad del cuerpo permanece modificada. La velocidad de un objeto cambia durante los marcos de tiempo, la velocidad promedio puede ser diferente de su velocidad real. El objeto alcanza la aceleración o desaceleración en el caso de un movimiento no uniforme. Por ejemplo, un automóvil que viaja 20 km en la primera hora, 30 km en la hora siguiente, y así sucesivamente con una velocidad variable a lo largo de su movimiento.

Ejemplos:

Una persona de carreras.
Una pelota que rebota a diferentes intervalos.
Dos coches chocando entre sí

Gráfico de tiempo de distancia para movimiento no uniforme

Aceleración

La aceleración se denomina como la tasa de cambio de la velocidad que se calcula como una función del tiempo. O en otras palabras, la aceleración se puede visualizar como la segunda derivada de la posición respecto al tiempo.

Es una cantidad vectorial , que está asociada tanto con la magnitud como con la dirección. Se denota por ‘ a ‘.

La unidad de aceleración es metros por segundo al cuadrado o metros por segundo (la rapidez o velocidad del objeto) por segundo o m/s ² .

La fórmula dimensional de la aceleración es [M ⁰ L ¹ T ^-2 ] .

La aceleración puede ser positiva, cero o negativa. En caso de que la velocidad del objeto aumente con el tiempo, se puede denominar aceleración positiva . En caso de que la velocidad sea cero, se denomina aceleración cero , mientras que la aceleración negativa también se conoce como retardo , lo que indica una disminución de la velocidad con el tiempo.

Matemáticamente, el cambio en la velocidad de un objeto en movimiento se define como (v – u) donde v y u son las velocidades final e inicial.

Por lo tanto, la aceleración del objeto está dada por,

Aceleración = Cambio de velocidad / Tiempo empleado

a = (v – u) / t

donde t es el tiempo que tarda el objeto.

Tipos de aceleración

Los siguientes son los diferentes tipos de aceleración asociados con un objeto como,

1. Aceleración promedio: la aceleración promedio se define como el cambio en la velocidad durante un intervalo de tiempo específico específico. La aceleración promedio se puede calcular para una instancia de tiempo, de la siguiente manera,

una _v = Δ v / Δ t

una _v = (v _f – v _yo ) / (t _f – t _yo )

donde v _f es la velocidad final, v _i es la velocidad inicial, ti _es el tiempo inicial y t _f es el tiempo final.

2. Aceleración instantánea: para calcular la aceleración instantánea, se puede calcular la velocidad promedio entre dos puntos en el tiempo separados por Δt y dejar que Δt se acerque a cero. El resultado obtenido es la derivada de la función de velocidad v(t), que es la aceleración instantánea. Matemáticamente,

$a(t)=\dfrac{d}{dt}v\left(t\right)$

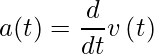
Así, al igual que la velocidad es la derivada de la función de posición, la aceleración instantánea es la derivada de la función de velocidad. Podemos mostrar esto gráficamente de la misma manera que la velocidad instantánea. En la (Figura), la aceleración instantánea en el tiempo t ₀ es la pendiente de la línea tangente a la gráfica de velocidad versus tiempo en el tiempo t ₀ . Vemos que la aceleración promedio dada como,

$\overline a=\dfrac{Δv}{Δt}$

Se acerca a la aceleración instantánea cuando Δt se acerca a cero. También en la parte (a) de la figura, se muestra la aceleración instantánea para el punto en la curva de velocidad a la velocidad máxima. Con un valor de pendiente de 0, se alcanza la velocidad máxima. Este tiempo corresponde al cero de la función de aceleración. En la parte (b), la aceleración instantánea a la velocidad mínima es cero, ya que la pendiente de la curva también es cero allí.

En el gráfico velocidad-tiempo, la aceleración instantánea es equivalente a la pendiente de la recta tangente.

(a) La aceleración promedio:

$\overline a=\frac{Δv}{Δt}=\frac{v_i-v_f}{t_i-t_f}$

Δt = t ₀ – t ₁ , Δt = t ₅ – t ₂ y Δt = t ₄ – t ₃

Cuando t ⇢ 0. Podemos concluir que la aceleración promedio se aproxima a la aceleración instantánea en el tiempo t ₀ .

Por lo tanto, para una función dada de velocidad-tiempo, el cero de la función de aceleración se alcanza a una velocidad mínima o máxima.

Varios gráficos relacionados con el movimiento (para aceleración)

Gráfica Desplazamiento-Tiempo

En este gráfico, el tiempo se representa en el eje x y el desplazamiento en el eje y. En el caso de un movimiento acelerado (a > 0), la pendiente de este gráfico aumenta con el tiempo, mientras que para el movimiento desacelerado, la pendiente disminuye

Gráfico de velocidad-tiempo

Las curvas indican el gráfico de velocidad-tiempo, el tiempo se traza a lo largo del eje x y la velocidad se traza a lo largo del eje y. Mientras encuentra el desplazamiento a través del gráfico v – t, mantenga el signo bajo consideración.

Cuando la velocidad de la partícula es constante o la aceleración es cero.

Cuando la partícula se mueve con una aceleración constante y su velocidad inicial es cero.

Cuando la partícula se mueve con retardo constante.

Cuando la partícula se mueve con aceleración no uniforme y su velocidad inicial es cero.

Cuando la aceleración disminuye y aumenta.

El área total encerrada por la curva tiempo-velocidad representa la distancia recorrida por un cuerpo.

Gráfico de aceleración-tiempo

Las curvas indican el gráfico de aceleración-tiempo donde el tiempo se traza a lo largo del eje X y la aceleración se traza a lo largo del eje Y. Puede presentarse el siguiente caso:

Cuando la aceleración de la partícula es cero.

Cuando la aceleración es constante

Cuando la aceleración es positivamente creciente

Cuando la aceleración es negativamente decreciente

Cuando la aceleración inicial es cero y la tasa de cambio de la aceleración no es uniforme

El cambio en la velocidad de la partícula = área encerrada por la curva de aceleración del tiempo.

Aceleración uniforme

En caso de que la velocidad de un objeto cambie en cantidades iguales durante el mismo intervalo de tiempo, se dice que el cuerpo tiene una aceleración uniforme. En este caso, ni la dirección ni la magnitud cambian con respecto al tiempo.

Ejemplos

Una pelota rodando por la pendiente.
Cuando un ciclista monta la bicicleta en una pendiente donde ambos pedales están enganchados.
Un niño deslizándose desde el control deslizante.
Movimiento de automóvil con velocidad constante, etc.

Aceleración variable o no uniforme

La aceleración variable es la velocidad del cuerpo que cambia en cantidades variables durante el mismo intervalo de tiempo. La aceleración variable entra en escena cuando la dirección o la magnitud o ambos cambios del objeto con respecto al tiempo.

Ejemplos:

Un coche cambiando de velocidad
Movimiento circular uniforme
Movimiento de péndulo con velocidad variable

Ecuaciones de movimiento para movimiento uniformemente acelerado

Para un objeto que cubra un movimiento uniformemente acelerado, las siguientes ecuaciones derivadas se pueden usar para relacionar el desplazamiento (x), el tiempo empleado (f), la velocidad inicial (u), la velocidad final (v) y la aceleración (a).

La ecuación gobierna las velocidades final e inicial v y u de un objeto que se mueve con una aceleración uniforme a: v = u + at, que se puede visualizar gráficamente como,

El área bajo esta curva es:

El área entre los instantes de tiempo, 0 y t están dadas por,

= Área del triángulo ABC+ Área del rectángulo OACD

$=\frac{1}{2}(v-u)t+ut$

Ahora,

El área bajo la curva v – t representa el desplazamiento.

Por lo tanto, el desplazamiento x del objeto es:

$x=\frac{1}{2}(v-u)t+ut$

Pero, tenemos,

v – tu = en

Por lo tanto,

$x=\frac{1}{2}at^2+ut$

$x=ut+\frac{1}{2}at^2$

La ecuación para el desplazamiento también se puede dar de la siguiente manera:

$x=\frac{v+u}{2}t=vt$

Anteriormente hemos derivado:

v = tu + en

$\frac{v+u}{a}=t$

Sustituyendo el valor de t en la ecuación por el desplazamiento obtenemos,

$x=\left(\frac{v+u}{2}\right)\left(\frac{v-u}{2}\right)\\ \Rightarrow x=\frac{v^2-u^2}{2a}\\ \Rightarrow v^2=u^2+2as$

Entonces, hemos derivado siguiendo la ecuación cinemática

v = u + en ……..(i)

$s=ut+\frac{1}{2}at^2\ \ \ \ \ \ \ ......(ii)\\ v^2=u^2+2as\ \ \ \ \ \ \ .......(iii)$

Dónde,

u es la velocidad inicial

v es la velocidad final

a es la aceleración y

s es la distancia recorrida en el intervalo de tiempo t.

El desplazamiento en un instante particular de tiempo (n ^-ésimo segundo del movimiento) está dado por

$\displaystyle S_{n^{th}}=u+\frac{1}{2}a(2n-1)$

Problemas de muestra

Problema 1: Si un Camión acelera de 6 m/s a 10 m/s en 10 s. ¿Calcular su aceleración?

Solución:

Dado que,

Velocidad inicial u = 6 m/s,

Velocidad final v = 10 m/s,

Tiempo empleado t = 10 s.

Tenemos que encontrar la Aceleración ‘a’

Aceleración, a = (v – u) / t

= (10 m/s – 6 m/s) / 10 s

= 0,4 m/ ^s2

Por tanto, la aceleración del camión es de 0,4 m/s ² .

Problema 2: Si se lanza una pelota desde la terraza de un edificio al suelo. Si la pelota tardó 6 s en tocar el suelo. ¿Encontrar la altura de la terraza desde el suelo?

Solución:

Dado que,

Velocidad inicial u = 0 {cuando la pelota estaba en reposo},

Tiempo que tarda la pelota en tocar el suelo t = 6 segundos

Aceleración debida a la gravedad a = g = 9,8 m/s ² ,

Distancia recorrida por la piedra = Altura del puente = s

La distancia recorrida por la pelota desde la terraza hasta el suelo.

$s=ut+\frac{1}{2}gt^2$

$s = 0 + \frac{1}{2} × 9.8 × 6 = 29.4\ m$

Por lo tanto,

La distancia de la terraza al suelo es de 29,4 m .

Problema 3: Si un hombre conduce un automóvil a 108 km/h, reduce la velocidad y lo lleva a 72 km/h en 5 s. Calcular el retardo del coche?

Solución:

Dado que,

Velocidad inicial u = 108 km/h

o

$108\times\frac{5}{18}=30\ m/s$

Velocidad final v = 72 km/h

o

$72\times\frac{5}{18}=20\ m/s$

Tiempo empleado = 5 segundos

Por lo tanto, la aceleración es,

$a=\frac{Final\ velocity\ -\ Initial\ velocity}{Time\ taken}\\ a=\frac{v\ -\ u}{t}\\ =\frac{20\ -\ 30}{5}\\ a = -2\ m/s^2$

Un signo negativo indica retraso.

Problema 4: Si un automóvil parte del reposo y luego acelera uniformemente a razón de 7,5 m/s ² durante 10 s. Encuentre la velocidad del tren en 10 s.

Solución:

Dado que,

Velocidad inicial u = 0 {ya que el automóvil estaba en reposo}

Aceleración a = 7,5 m/s ²

Tiempo t = 10 s

v = tu + en

= 0 + 7,5 × 10

Problema 5: Si un objeto se mueve a lo largo del eje x según la relación x = 1 – 2t + 3t ² , donde x está en metros y t en segundos. Calcula la aceleración del cuerpo cuando t = 3s.

Solución:

Dado que,

x = 1 – 2t + 3t ²

Velocidad, v = dx/dt

= d/dt {1 – 2t + 3t ² }

= -2 + 6t

Por lo tanto, Aceleración a = dv/dt

= d/dt {-2 + 6t}

= 6 m/s ²

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

¿Qué es el movimiento en línea recta?

Aceleración

Tipos de aceleración

Problemas de muestra

Deja una respuesta Cancelar la respuesta