¿Qué es un condensador de placas paralelas?

Posted on by Rudeus Greyrat

La capacitancia se puede definir en términos de Layman como una cantidad física que indica la capacidad de un componente o circuito para recolectar y almacenar energía en forma de carga eléctrica. Entonces podemos decir que un capacitor es un componente eléctrico que extrae energía de una batería y almacena la energía. Luego, los terminales se pueden conectar a un circuito que tenga cierta resistencia de carga. Cuando se hace esto, el condensador libera rápidamente electricidad en una pequeña fracción de segundo. Un condensador se puede hacer de cualquier manera, sin embargo, siempre hay dos requisitos que deben cumplirse 

  • Debe estar hecho de dos terminales que sean de naturaleza conductora.
  • Debe haber algún espacio entre los dos terminales y ese espacio debe llenarse con un dieléctrico (aislante).

Por lo general, en un capacitor, las dos terminales están hechas de algún material conductor, como una lámina delgada de aluminio, y el dieléctrico puede estar hecho de vidrio, mica o incluso aire. Un capacitor tiene muchas características que lo hacen una parte importante de un circuito.

  • Dado que la carga se almacena directamente en las placas, el proceso de carga y descarga se vuelve simple y fácil.
  • Se utiliza como filtro ya que permite que fluya CA pero no CC
  • El condensador puede soportar una gran diferencia de potencial en un circuito y no romperse.
  • Los condensadores son útiles para filtrar las frecuencias no deseadas.

Funcionamiento de un condensador 

Considere una configuración de dos terminales separados por cierta distancia y hay algún medio (de naturaleza aislante) entre ellos ahora que pasamos corriente a través de ellos, la corriente no fluirá debido al hecho de que hay algún material aislante que separa estos dos terminales de cada uno otro. La configuración continúa cargándose durante bastante tiempo, de modo que ambos terminales obtienen cargas opuestas y luego llega a un estado en el que ha alcanzado un punto de carga máxima. La configuración se denomina condensador y este período de tiempo se denomina tiempo de carga del condensador. 

Fig. 1. Un capacitor está conectado a una batería.

Más tarde, podemos quitar la batería del capacitor y luego colocar una resistencia de carga en ese circuito. Esto conduciría al capacitor a actuar como una batería en un circuito cerrado y la corriente fluiría desde la terminal con carga positiva del capacitor hacia la terminal con carga negativa. del capacitor Y con el tiempo el capacitor perdería todas sus cargas. El período de tiempo en el que pierde todas sus cargas se denomina período de descarga del condensador.

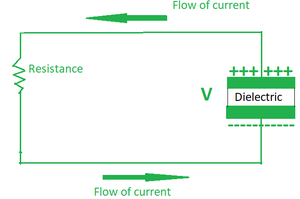
Fig. 2. Fase de descarga de un condensador.

Así podemos decir que un capacitor es un dispositivo que puede almacenar carga y a su vez energía en sí mismo. 

Capacitancia de un conductor

Considere un capacitor cuyas placas positiva y negativa tienen carga +q y -q respectivamente. Se aplica una fuente de voltaje de CC a través de él, lo que le da una diferencia de potencial de V a través de las placas. Ahora bien, como sabemos,

 Q ∝ V

Poniendo una constante C en esta relación.

Q = CV.

Nota: La capacitancia de cada material es única y su unidad SI es Farad (F). 

Condensador de placas paralelas

Considere una configuración dada de dos placas que están conectadas a través de una batería, la disposición es tal que ambas placas tienen las mismas dimensiones físicas y ambas están colocadas paralelas entre sí y separadas por cierta distancia. La separación entre las dos placas se rellena con algo de dieléctrico. Las dos placas también tienen carga opuesta ya que la placa conectada a la terminal positiva adquiere una carga positiva y la placa conectada a la terminal negativa adquiere una carga negativa.

Fig. 3. Un capacitor simple de placas paralelas.

En nuestro caso, el área de ambas placas es A y la carga sobre ellas es +Q y -Q. Además, la distancia entre ellos está dada por d, que es despreciablemente pequeña en comparación con el área de las placas, por lo que podemos decir que d<<A. 

Ahora desde d<<A.

Por lo tanto, ambas placas pueden considerarse como láminas planas infinitas.

La densidad de carga superficial de una placa cargada positivamente puede estar dada por 

σ = \frac{Q}{A}  .

La densidad de carga superficial de una placa cargada negativamente puede estar dada por

σ = \frac{-Q}{A}  .

Supongamos que el capacitor de placas paralelas divide las placas en tres regiones de tal manera que,

  • La región a la izquierda de la placa cargada positivamente es la Región 1.
  • La región en el medio de las dos placas es la región 2.
  • Y la región a la derecha de la placa cargada negativamente es la región 3.

Figura 4. El avión se divide en tres regiones.

Ahora calculemos los campos eléctricos en cada una de las tres regiones por separado.

  • Región 1:

Usando la ley de Gauss, el campo eléctrico generado por una lámina infinita viene dado por:

E = \frac{\sigma}{2\epsilon}  .

El campo eléctrico generado por ambas placas en la región 1 es de la misma magnitud y dirección opuesta.

mi = mi 1 + mi 2 

E = \frac{\sigma}{2ε} - \frac{\sigma}{2ε}  .

mi = 0

  • Región 2:

En este caso calculamos el campo eléctrico entre las dos placas. 

Aquí la magnitud y la dirección del campo eléctrico son las mismas. Entonces, el campo eléctrico generado viene dado por: –

mi = \frac{\sigma}{2\epsilon} + \frac{\sigma}{2\epsilon}   

E = \frac{\sigma}{\epsilon}  .

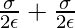
  • Región 3:

Esta región está a la derecha de la placa cargada negativamente.

El campo eléctrico en este caso está dado por

mi =  \frac{\sigma}{2\epsilon} - \frac{\sigma}{2\epsilon}  .

mi = 0

Ahora la expresión para la capacitancia se da como:

C = \frac{Q}{V}  . ⇢ (1)

El valor de la diferencia de potencial V se puede encontrar usando la fórmula,

V = mi × re.

V = \frac{Qd}{A\epsilon}  . ⇢ (2)

Entonces, la capacitancia del capacitor de placas paralelas puede estar dada por

De (1) y (2),

C = \frac{\epsilon A}{d}  .

Ejemplos de preguntas

Pregunta 1: Un condensador de placas paralelas se coloca en el aire. Encuentre su capacitancia si el área de cada placa es de 100 cm 2 y la separación entre las placas es de 1 cm.

Solución:

 La capacitancia del capacitor de placas paralelas se puede dar como,

C = \frac{\epsilon A}{d}  .

Aquí A = 100 × 10 -4 m 2 , d= 10 -2 m.

C = \frac{8.85\times10^{-12} \times100\times 10^{-4}}{10^{-2}}  

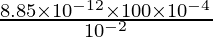
C = 8,85 × 10 -12 F.

Pregunta 2: Un capacitor de 100 cm^2 de área genera una capacitancia de 17.7 × 10 -11 F . Averigüe la separación entre las placas de este capacitor.

Solución:

C = \frac{\epsilon A}{d}

Aquí A = 100 × 10 -4 m , C = 17,7 × 10 -11 F  

 17,7 × 10 -11  =  \frac{8.85\times10^{-12}\times 100\times 10^{-4}}{d}   

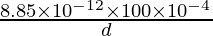
d = 5 × 10 -4   m.

Pregunta 3: El área de un capacitor de placas paralelas se duplica y la separación entre las placas se reduce a la mitad para averiguar el cambio en su capacitancia.

Solución:

C1 =  _\frac{\epsilon A}{d}    

Según pregunta,

d 2 = \frac{1}{2}d_1  

UN 2 = 2 UN 1 

do2 =  _ \frac{\epsilon^2 A_1}{\frac{1}{2}d_1}    

C2 =  4 \frac{\epsilon A_1}{d_1}   

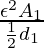
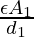
C 2 = 4 C 1  

Pregunta 4: Un capacitor de placas paralelas con un área de placas de 100 cm 2 y una separación entre las placas de 1 cm se coloca en el aire y se le da un voltaje de 1000V Halla su energía

Solución:

La capacitancia del capacitor de placas paralelas se puede dar como,

C = \frac{\epsilon A}{d}  

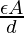
Aquí A = 100 × 10 -4 m 2 , d = 10 -2 m 

C = \frac{8.85\times10^{-12}\times 100\times 10^{-4}}{10^{-2}}   

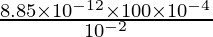
C = 8,85 × 10 -12 F.

La energía de este capacitor se puede calcular usando la expresión

U = 1/2 VC 2

tu = \frac{1}{2}\times8.85\times10^{-12}\times1000^2   

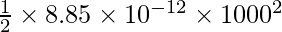
U = 4,425 × 10 -6  J

Pregunta 5: La capacitancia de un capacitor de placas paralelas es 4.425 × 10 -12 F. La separación entre las placas es de 1 cm. Encuentra el área de cada placa.

Solución:

La capacitancia del capacitor de placas paralelas se puede dar como

C = \frac{\epsilon A}{d}

Aquí C = 4.425 × 10 -12 F , d= 10 -2 m

4,425 × 10 -12 = 8,85 × 10 -12 × A/10 -2    .

un = \frac{10^{-2}}{2}   

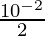
A = 5 × 10 -3 m 2

Pregunta 6: Un condensador de placas paralelas se coloca en el aire. Encuentre su capacitancia si el área de cada placa es de 100 cm 2 y la separación entre las placas es de 1 cm. Si se suministra un voltaje de 100 V, ¿cuánta carga almacenará el capacitor?

Solución:

 la capacitancia del capacitor de placas paralelas se puede dar como

C = \frac{\epsilon A}{d}  

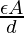
Aquí A = 100 × 10 -4 m 2 , d = 10 -2 m.

C = \frac{8.85\times10^{-12} \times100\times 10^{-4}}{10^{-2}}    .

C= 8,85 × 10 -12    F. 

La carga de un capacitor viene dada por

Q = CV.

Q = 8,85 × 10 -12 × 100 C.

Q = 8,85 × 10 -10  

Pregunta 7: La separación entre las placas de un capacitor de placas paralelas se llena con un material de permitividad relativa cinco veces mayor que la del aire. Halle su capacitancia si la separación entre las placas es de 1 cm y el área de cada placa es de 200 cm 2.

Solución:

 la capacitancia del capacitor de placas paralelas se puede dar como

C = \frac{\epsilon A}{d}

Aquí A = 200 × 10 -4 m 2 , d = 10 -2 m .

ε = 5 × 8,85 × 10 -12  .

C = \frac{5\times 8.85\times10^{-12} \times 200\times 10^{-4}}{10^{-2}}    .

C = 8,85 × 10 -11 F .

Publicación traducida automáticamente

Artículo escrito por harmansahani100 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *