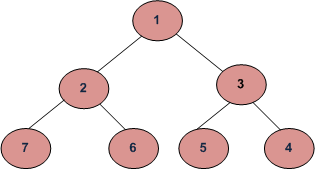
Escriba una función para imprimir el recorrido en espiral de un árbol. Para el siguiente árbol, la función debe imprimir 1, 2, 3, 4, 5, 6, 7.
Hemos discutido el enfoque ingenuo y el enfoque basado en dos pilas en Level Order con recursividad y pilas múltiples.
La idea detrás de este enfoque es que primero tenemos que tomar una cola, una bandera de dirección y una bandera de separación que es NULL
- Inserte el elemento raíz en la cola y vuelva a insertar NULL en la cola.
- Para cada elemento de la cola, inserte sus Nodes secundarios.
- Si se encuentra un NULL, verifique que la dirección para atravesar el nivel en particular sea de izquierda a derecha o de derecha a izquierda. Si es un nivel par, atraviese de izquierda a derecha; de lo contrario, atraviese el árbol de derecha a nivel, es decir, desde el frente hasta el frente anterior, es decir, desde el NULL actual hasta el último NULL que se ha visitado. Esto continúa hasta el último nivel, luego se rompe el bucle e imprimimos lo que queda (que no se ha impreso) comprobando la dirección de impresión.
A continuación se muestra la implementación de la explicación.
C++
// C++ program to print level order traversal
// in spiral form using a single dequeue
#include <bits/stdc++.h>
struct Node {
int data;
struct Node *left, *right;
};
// A utility function to create a new node
struct Node* newNode(int data)
{
struct Node* node = new struct Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
// function to print the level order traversal
void levelOrder(struct Node* root, int n)
{
// We can just take the size as H+N which
// implies the height of the tree with the
// size of the tree
struct Node* queue[2 * n];
int top = -1;
int front = 1;
queue[++top] = NULL;
queue[++top] = root;
queue[++top] = NULL;
// struct Node* t=root;
int prevFront = 0, count = 1;
while (1) {
struct Node* curr = queue[front];
// A level separator found
if (curr == NULL) {
// If this is the only item in dequeue
if (front == top)
break;
// Else print contents of previous level
// according to count
else {
if (count % 2 == 0) {
for (int i = prevFront + 1; i < front; i++)
printf("%d ", queue[i]->data);
}
else {
for (int i = front - 1; i > prevFront; i--)
printf("%d ", queue[i]->data);
}
prevFront = front;
count++;
front++;
// Insert a new level separator
queue[++top] = NULL;
continue;
}
}
if (curr->left != NULL)
queue[++top] = curr->left;
if (curr->right != NULL)
queue[++top] = curr->right;
front++;
}
if (count % 2 == 0) {
for (int i = prevFront + 1; i < top; i++)
printf("%d ", queue[i]->data);
}
else {
for (int i = top - 1; i > prevFront; i--)
printf("%d ", queue[i]->data);
}
}
// Driver code
int main()
{
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
levelOrder(root, 7);
return 0;
}
Java
// Java program to print level order traversal
// in spiral form using a single dequeue
class Solution
{
static class Node
{
int data;
Node left, right;
};
// A utility function to create a new node
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null;
return (node);
}
// function to print the level order traversal
static void levelOrder( Node root, int n)
{
// We can just take the size as H+N which
// implies the height of the tree with the
// size of the tree
Node queue[] = new Node[2 * n];
for(int i = 0; i < 2 * n; i++)
queue[i] = new Node();
int top = -1;
int front = 1;
queue[++top] = null;
queue[++top] = root;
queue[++top] = null;
// Node t=root;
int prevFront = 0, count = 1;
while (true)
{
Node curr = queue[front];
// A level separator found
if (curr == null)
{
// If this is the only item in dequeue
if (front == top)
break;
// Else print contents of previous level
// according to count
else
{
if (count % 2 == 0)
{
for (int i = prevFront + 1; i < front; i++)
System.out.printf("%d ", queue[i].data);
}
else
{
for (int i = front - 1; i > prevFront; i--)
System.out.printf("%d ", queue[i].data);
}
prevFront = front;
count++;
front++;
// Insert a new level separator
queue[++top] = null;
continue;
}
}
if (curr.left != null)
queue[++top] = curr.left;
if (curr.right != null)
queue[++top] = curr.right;
front++;
}
if (count % 2 == 0)
{
for (int i = prevFront + 1; i < top; i++)
System.out.printf("%d ", queue[i].data);
}
else
{
for (int i = top - 1; i > prevFront; i--)
System.out.printf("%d ", queue[i].data);
}
}
// Driver code
public static void main(String args[])
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
levelOrder(root, 7);
}
}
// This code is contributed by Arnab Kundu
C#
// C# program to print level order traversal
// in spiral form using a single dequeue
using System;
class GFG
{
public class Node
{
public int data;
public Node left, right;
};
// A utility function to create a new node
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null;
return (node);
}
// function to print the level order traversal
static void levelOrder( Node root, int n)
{
// We can just take the size as H+N which
// implies the height of the tree with the
// size of the tree
Node []queue = new Node[2 * n];
for(int i = 0; i < 2 * n; i++)
queue[i] = new Node();
int top = -1;
int front = 1;
queue[++top] = null;
queue[++top] = root;
queue[++top] = null;
// Node t=root;
int prevFront = 0, count = 1;
while (true)
{
Node curr = queue[front];
// A level separator found
if (curr == null)
{
// If this is the only item in dequeue
if (front == top)
break;
// Else print contents of previous level
// according to count
else
{
if (count % 2 == 0)
{
for (int i = prevFront + 1;
i < front; i++)
Console.Write(" " + queue[i].data);
}
else
{
for (int i = front - 1;
i > prevFront; i--)
Console.Write(" " + queue[i].data);
}
prevFront = front;
count++;
front++;
// Insert a new level separator
queue[++top] = null;
continue;
}
}
if (curr.left != null)
queue[++top] = curr.left;
if (curr.right != null)
queue[++top] = curr.right;
front++;
}
if (count % 2 == 0)
{
for (int i = prevFront + 1; i < top; i++)
Console.Write(" " + queue[i].data);
}
else
{
for (int i = top - 1; i > prevFront; i--)
Console.Write(" " + queue[i].data);
}
}
// Driver code
public static void Main(String []args)
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
levelOrder(root, 7);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// Javascript program to print level order
// traversal in spiral form using a single dequeue
class Node
{
constructor()
{
this.data = 0;
this.left = null;
this.right = null;
}
};
// A utility function to create a new node
function newNode(data)
{
var node = new Node();
node.data = data;
node.left = node.right = null;
return (node);
}
// Function to print the level order traversal
function levelOrder(root, n)
{
// We can just take the size as H+N which
// implies the height of the tree with the
// size of the tree
var queue = Array(2 * n);
for(var i = 0; i < 2 * n; i++)
queue[i] = new Node();
var top = -1;
var front = 1;
queue[++top] = null;
queue[++top] = root;
queue[++top] = null;
// Node t=root;
var prevFront = 0, count = 1;
while (true)
{
var curr = queue[front];
// A level separator found
if (curr == null)
{
// If this is the only item in dequeue
if (front == top)
break;
// Else print contents of previous level
// according to count
else
{
if (count % 2 == 0)
{
for(var i = prevFront + 1;
i < front; i++)
document.write(" " + queue[i].data);
}
else
{
for(var i = front - 1;
i > prevFront; i--)
document.write(" " + queue[i].data);
}
prevFront = front;
count++;
front++;
// Insert a new level separator
queue[++top] = null;
continue;
}
}
if (curr.left != null)
queue[++top] = curr.left;
if (curr.right != null)
queue[++top] = curr.right;
front++;
}
if (count % 2 == 0)
{
for(var i = prevFront + 1; i < top; i++)
document.write(" " + queue[i].data);
}
else
{
for(var i = top - 1; i > prevFront; i--)
document.write(" " + queue[i].data);
}
}
// Driver code
var root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
levelOrder(root, 7);
// This code is contributed by rutvik_56
</script>
Producción:
1 2 3 4 5 6 7
Complejidad temporal: O(n)
Espacio auxiliar: O(2*n) = O(n)
Publicación traducida automáticamente
Artículo escrito por devarajakhil matta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA