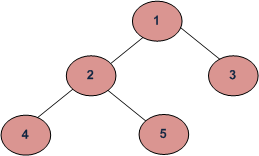
Dado un árbol binario, atravesarlo usando DFS usando recursividad.
A diferencia de las estructuras de datos lineales (array, lista enlazada, colas, pilas, etc.) que solo tienen una forma lógica de atravesarlos, los árboles se pueden recorrer de diferentes maneras. En general, hay 2 formas ampliamente utilizadas para atravesar árboles:
- DFS o primera búsqueda en profundidad
- BFS o búsqueda primero en amplitud
En este artículo, se ha discutido el recorrido mediante DFS. Consulte esta publicación para Breadth First Traversal.
Búsqueda en profundidad
DFS (búsqueda primero en profundidad) es una técnica utilizada para recorrer árboles o gráficos. Aquí se utiliza el retroceso para el recorrido. En este recorrido primero se visita el Node más profundo y luego retrocede a su Node principal si no existe un hermano de ese Node.
Recorrido DFS de un gráfico frente a un árbol
En el gráfico, puede haber ciclos y desconexión. A diferencia del gráfico, el árbol no contiene ciclos y siempre está conectado. Entonces, el DFS de un árbol es relativamente más fácil. Simplemente podemos comenzar desde un Node, luego atravesar sus adyacentes (o hijos) sin preocuparnos por los ciclos. Y si comenzamos desde un solo Node (raíz) y recorremos de esta manera, está garantizado que recorremos todo el árbol ya que no hay desconexión,
Ejemplos:
Árbol:
Por lo tanto, los primeros recorridos en profundidad de este árbol serán:
(a) En orden (Izquierda, Raíz, Derecha): 4 2 5 1 3
(b) Preorden (Raíz, Izquierda, Derecha): 1 2 4 5 3
(c) Posorden (Izquierda, Derecha, Raíz) : 4 5 2 3 1
A continuación se muestran los recorridos de árbol a través de DFS usando recursividad:
1. Recorrido en Orden ( Práctica ):
Ejemplo: el recorrido en orden para la figura anterior es 4 2 5 1 3.
Algorithm Inorder(tree) 1. Traverse the left subtree, i.e., call Inorder(left-subtree) 2. Visit the root. 3. Traverse the right subtree, i.e., call Inorder(right-subtree)
Implementación:
C++
// C program for different tree traversals
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node {
int data;
struct Node *left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout << node->data << " ";
/* now recur on right child */
printInorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "\nInorder traversal of binary tree is \n";
printInorder(root);
return 0;
}
C
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%d ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("\nInorder traversal of binary tree is \n");
printInorder(root);
getchar();
return 0;
}
Java
// Java program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(Node node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
System.out.print(node.key + " ");
/* now recur on right child */
printInorder(node.right);
}
// Wrappers over above recursive functions
void printInorder() { printInorder(root); }
// Driver method
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("\nInorder traversal of binary tree is ");
tree.printInorder();
}
}
Python
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "\nInorder traversal of binary tree is" printInorder(root)
C#
// C# program for different tree traversals
using System;
/* Class containing left and right child of current
node and key value*/
class Node
{
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(Node node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
Console.Write(node.key + " ");
/* now recur on right child */
printInorder(node.right);
}
// Wrappers over above recursive functions
void printInorder()
{
printInorder(root);
}
// Driver code
public static void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("\nInorder traversal of binary tree is ");
tree.printInorder();
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// javascript program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
/* Given a binary tree, print its nodes in inorder */
function printInorder(node) {
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
document.write(node.key + " ");
/* now recur on right child */
printInorder(node.right);
}
// Driver method
var root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write("<br/>Inorder traversal of binary tree is <br/>");
printInorder(root);
// This code is contributed by umadevi9616
</script>
Inorder traversal of binary tree is 4 2 5 1 3
Usos de Inorder:
en el caso de árboles de búsqueda binarios (BST), el recorrido Inorder proporciona Nodes en orden no decreciente. Para obtener Nodes de BST en orden no creciente, se puede usar una variación de Inorder traversal donde Inorder traversal s invertido.
2. Recorrido de preorden ( práctica ):
Ejemplo: el recorrido de preorden para la cifra anterior es 1 2 4 5 3.
Algorithm Preorder(tree) 1. Visit the root. 2. Traverse the left subtree, i.e., call Preorder(left-subtree) 3. Traverse the right subtree, i.e., call Preorder(right-subtree)
Implementación:
C++
// C program for different tree traversals
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node {
int data;
struct Node *left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
/* first print data of node */
cout << node->data << " ";
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "\nPreorder traversal of binary tree is \n";
printPreorder(root);
return 0;
}
C
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct node* node)
{
if (node == NULL)
return;
/* first print data of node */
printf("%d ", node->data);
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("\nPreorder traversal of binary tree is \n");
printPreorder(root);
getchar();
return 0;
}
Java
// Java program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(Node node)
{
if (node == null)
return;
/* first print data of node */
System.out.print(node.key + " ");
/* then recur on left subtree */
printPreorder(node.left);
/* now recur on right subtree */
printPreorder(node.right);
}
// Wrappers over above recursive functions
void printPreorder() { printPreorder(root); }
// Driver method
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Preorder traversal of binary tree is ");
tree.printPreorder();
}
}
Python
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "Preorder traversal of binary tree is" printPreorder(root)
C#
// C# program for different tree traversals
using System;
/* Class containing left and right child of current
node and key value*/
public class Node
{
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(Node node)
{
if (node == null)
return;
/* first print data of node */
Console.Write(node.key + " ");
/* then recur on left subtree */
printPreorder(node.left);
/* now recur on right subtree */
printPreorder(node.right);
}
// Wrappers over above recursive functions
void printPreorder() { printPreorder(root); }
// Driver method
public static void Main()
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Preorder traversal of binary tree is ");
tree.printPreorder();
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// JavaScript implementation of above approach
// A class that represents an individual node in a
// Binary Tree
class Node{
constructor(key){
this.left = null
this.right = null
this.val = key
}
}
// A function to do preorder tree traversal
function printPreorder(root){
if(root){
// First print the data of node
document.write(root.val," ")
// Then recur on left child
printPreorder(root.left)
// Finally recur on right child
printPreorder(root.right)
}
}
// Driver code
let root = new Node(1)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(4)
root.left.right = new Node(5)
document.write("Preorder traversal of binary tree is","</br>")
printPreorder(root)
// This code is contributed by shinjanpatra
</script>
Preorder traversal of binary tree is 1 2 4 5 3
Usos del pedido anticipado:
el recorrido del pedido anticipado se usa para crear una copia del árbol. El recorrido de preorden también se usa para obtener una expresión de prefijo en un árbol de expresión. Consulte http://en.wikipedia.org/wiki/Polish_notation para saber por qué son útiles las expresiones de prefijo.
3. Recorrido Posorden ( Práctica ):
Ejemplo: el recorrido posterior al orden para el árbol anterior es 4 5 2 3 1.
Algorithm Postorder(tree) 1. Traverse the left subtree, i.e., call Postorder(left-subtree) 2. Traverse the right subtree, i.e., call Postorder(right-subtree) 3. Visit the root.
Implementación:
C++
// C program for different tree traversals
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node {
int data;
struct Node *left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct Node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
cout << node->data << " ";
}
/* Driver program to test above functions*/
int main()
{
struct Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "\nPostorder traversal of binary tree is \n";
printPostorder(root);
return 0;
}
C
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
printf("%d ", node->data);
}
/* Driver program to test above functions*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("\nPostorder traversal of binary tree is \n");
printPostorder(root);
getchar();
return 0;
}
Java
// Java program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(Node node)
{
if (node == null)
return;
// first recur on left subtree
printPostorder(node.left);
// then recur on right subtree
printPostorder(node.right);
// now deal with the node
System.out.print(node.key + " ");
}
// Wrappers over above recursive functions
void printPostorder() { printPostorder(root); }
// Driver method
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("\nPostorder traversal of binary tree is ");
tree.printPostorder();
}
}
Python
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "\nPostorder traversal of binary tree is" printPostorder(root)
C#
// C# program for different tree traversals
using System;
/* Class containing left and right child of current
node and key value*/
public class Node
{
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(Node node)
{
if (node == null)
return;
// first recur on left subtree
printPostorder(node.left);
// then recur on right subtree
printPostorder(node.right);
// now deal with the node
Console.Write(node.key + " ");
}
// Wrappers over above recursive functions
void printPostorder() { printPostorder(root); }
// Driver code
public static void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("\nPostorder traversal of binary tree is ");
tree.printPostorder();
}
}
// This code contributed by Rajput-Ji
Javascript
<script>
// javascript program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
constructor(item) {
this.key = item;
this.left = this.right = null;
}
}
var root;
/*
* Given a binary tree, print its nodes according to the "bottom-up" postorder
* traversal.
*/
function printPostorder(node) {
if (node == null)
return;
// first recur on left subtree
printPostorder(node.left);
// then recur on right subtree
printPostorder(node.right);
// now deal with the node
document.write(node.key + " ");
}
// Driver method
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write("\nPostorder traversal of binary tree is<br/> ");
printPostorder(root);
// This code contributed by umadevi9616
</script>
Postorder traversal of binary tree is 4 5 2 3 1
Usos de Postorder:
Postorder transversal se utiliza para eliminar el árbol. Consulte la pregunta sobre la eliminación del árbol para obtener más información. El recorrido de orden posterior también es útil para obtener la expresión de posfijo de un árbol de expresión. Consulte http://en.wikipedia.org/wiki/Reverse_Polish_notation para ver el uso de la expresión postfix.
Implementando todos los cruces usando DFS
C++
// C program for different tree traversals
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct Node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
cout << node->data << " ";
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout << node->data << " ";
/* now recur on right child */
printInorder(node->right);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
/* first print data of node */
cout << node->data << " ";
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "\nPreorder traversal of binary tree is \n";
printPreorder(root);
cout << "\nInorder traversal of binary tree is \n";
printInorder(root);
cout << "\nPostorder traversal of binary tree is \n";
printPostorder(root);
return 0;
}
C
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
printf("%d ", node->data);
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%d ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct node* node)
{
if (node == NULL)
return;
/* first print data of node */
printf("%d ", node->data);
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("\nPreorder traversal of binary tree is \n");
printPreorder(root);
printf("\nInorder traversal of binary tree is \n");
printInorder(root);
printf("\nPostorder traversal of binary tree is \n");
printPostorder(root);
getchar();
return 0;
}
Java
// Java program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node
{
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(Node node)
{
if (node == null)
return;
// first recur on left subtree
printPostorder(node.left);
// then recur on right subtree
printPostorder(node.right);
// now deal with the node
System.out.print(node.key + " ");
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(Node node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
System.out.print(node.key + " ");
/* now recur on right child */
printInorder(node.right);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(Node node)
{
if (node == null)
return;
/* first print data of node */
System.out.print(node.key + " ");
/* then recur on left subtree */
printPreorder(node.left);
/* now recur on right subtree */
printPreorder(node.right);
}
// Wrappers over above recursive functions
void printPostorder() { printPostorder(root); }
void printInorder() { printInorder(root); }
void printPreorder() { printPreorder(root); }
// Driver method
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Preorder traversal of binary tree is ");
tree.printPreorder();
System.out.println("\nInorder traversal of binary tree is ");
tree.printInorder();
System.out.println("\nPostorder traversal of binary tree is ");
tree.printPostorder();
}
}
Python
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "Preorder traversal of binary tree is" printPreorder(root) print "\nInorder traversal of binary tree is" printInorder(root) print "\nPostorder traversal of binary tree is" printPostorder(root)
C#
// C# program for different Console.Writetree traversals
using System;
/* Class containing left and right child of current
node and key value*/
public class Node
{
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree()
{
root = null;
}
/* Given a binary tree, print
its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(Node node)
{
if (node == null)
return;
// first recur on left subtree
printPostorder(node.left);
// then recur on right subtree
printPostorder(node.right);
// now deal with the node
Console.Write(node.key + " ");
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(Node node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
Console.Write(node.key + " ");
/* now recur on right child */
printInorder(node.right);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(Node node)
{
if (node == null)
return;
/* first print data of node */
Console.Write(node.key + " ");
/* then recur on left subtree */
printPreorder(node.left);
/* now recur on right subtree */
printPreorder(node.right);
}
// Wrappers over above recursive functions
void printPostorder() { printPostorder(root); }
void printInorder() { printInorder(root); }
void printPreorder() { printPreorder(root); }
// Driver code
public static void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Preorder traversal of binary tree is ");
tree.printPreorder();
Console.WriteLine("\nInorder traversal of binary tree is ");
tree.printInorder();
Console.WriteLine("\nPostorder traversal of binary tree is ");
tree.printPostorder();
}
}
// This code has been contributed by 29AjayKumar
Javascript
<script>
// JavaScript program to for tree traversals
// A class that represents an individual node in a
// Binary Tree
class Node{
constructor(key){
this.left = null
this.right = null
this.val = key
}
}
// A function to do inorder tree traversal
function printInorder(root){
if(root){
// First recur on left child
printInorder(root.left)
// then print the data of node
document.write(root.val," ")
// now recur on right child
printInorder(root.right)
}
}
// A function to do postorder tree traversal
function printPostorder(root){
if(root){
// First recur on left child
printPostorder(root.left)
// the recur on right child
printPostorder(root.right)
// now print the data of node
document.write(root.val," ")
}
}
// A function to do preorder tree traversal
function printPreorder(root){
if(root){
// First print the data of node
document.write(root.val," ")
// Then recur on left child
printPreorder(root.left)
// Finally recur on right child
printPreorder(root.right)
}
}
// Driver code
let root = new Node(1)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(4)
root.left.right = new Node(5)
document.write("Preorder traversal of binary tree is","</br>")
printPreorder(root)
document.write("</br>","Inorder traversal of binary tree is","</br>")
printInorder(root)
document.write("</br>","Postorder traversal of binary tree is","</br>")
printPostorder(root)
// This code is contributed by shinjanpatra
</script>
Producción:
Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1
Complejidad de tiempo: O(n)
Espacio auxiliar: si no consideramos el tamaño de la pila para las llamadas a funciones, entonces O(1), de lo contrario, O(n).
Publicación traducida automáticamente
Artículo escrito por Shahnawaz_Ali y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA