Recuento de subsecuencias de longitud K cuyo producto es par

Dada una array arr[] y un entero K , la tarea es encontrar el número de subsecuencias no vacías de longitud K a partir de la array dada arr de tamaño N tal que el producto de la subsecuencia sea un número par.
Ejemplo:
 

Entrada: arr[] = [2, 3, 1, 7], K = 3 
Salida: 3 
Explicación: 
Hay 3 subsecuencias de longitud 3 cuyo producto es número par {2, 3, 1}, {2, 3, 7 }, {2, 1, 7}. 
Entrada: arr[] = [2, 4], K = 1 
Salida: 2 
Explicación: 
Hay 2 subsecuencias de longitud 1 cuyo producto es un número par {2} {4}. 
 

Enfoque:
Para resolver el problema mencionado anteriormente, tenemos que encontrar el número total de subsecuencias de longitud K y restar el número de subsecuencias de longitud K cuyo producto es impar. 
 

1. Para hacer un producto de la subsecuencia impar debemos elegir K números como impares.
2. Entonces, el número de subsecuencias de longitud K cuyo producto es impar posiblemente sea encontrar k números impares , es decir, “ o elige k ” o 
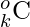
   donde o es el conteo de números impares en la subsecuencia.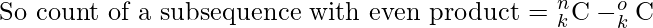
3. 
   donde n y o es el conteo de números totales y números impares respectivamente.

A continuación se muestra la implementación del programa anterior: 
 

// C++ implementation to Count of K
// length subsequence whose
// Product is even
 
#include <bits/stdc++.h>
using namespace std;
 
int fact(int n);
 
// Function to calculate nCr
int nCr(int n, int r)
{
    if (r > n)
        return 0;
    return fact(n)
           / (fact(r)
              * fact(n - r));
}
 
// Returns factorial of n
int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
 
// Function for finding number
// of K length subsequences
// whose product is even number
int countSubsequences(
    int arr[], int n, int k)
{
    int countOdd = 0;
 
    // counting odd numbers in the array
    for (int i = 0; i < n; i++) {
        if (arr[i] & 1)
            countOdd++;
    }
    int ans = nCr(n, k)
              - nCr(countOdd, k);
 
    return ans;
}
 
// Driver code
int main()
{
 
    int arr[] = { 2, 4 };
    int K = 1;
 
    int N = sizeof(arr) / sizeof(arr[0]);
 
    cout << countSubsequences(arr, N, K);
 
    return 0;
}

// Java implementation to count of K
// length subsequence whose product
// is even
import java.util.*;
 
class GFG{
     
// Function to calculate nCr
static int nCr(int n, int r)
{
    if (r > n)
        return 0;
    return fact(n) / (fact(r) *
                      fact(n - r));
}
 
// Returns factorial of n
static int fact(int n)
{
    int res = 1;
    for(int i = 2; i <= n; i++)
        res = res * i;
         
    return res;
}
 
// Function for finding number
// of K length subsequences
// whose product is even number
static int countSubsequences(int arr[],
                             int n, int k)
{
    int countOdd = 0;
 
    // Counting odd numbers in the array
    for(int i = 0; i < n; i++)
    {
        if (arr[i] % 2 == 1)
            countOdd++;
    }
    int ans = nCr(n, k) - nCr(countOdd, k);
 
    return ans;
}
 
// Driver code
public static void main(String args[])
{
    int arr[] = { 2, 4 };
    int K = 1;
 
    int N = arr.length;
 
    System.out.println(countSubsequences(arr, N, K));
}
}
 
// This code is contributed by ANKITKUMAR34

# Python3 implementation to Count of K
# length subsequence whose
# Product is even
 
# Function to calculate nCr
def nCr(n, r):
     
    if (r > n):
        return 0
    return fact(n) // (fact(r) *
                       fact(n - r))
 
# Returns factorial of n
def fact(n):
     
    res = 1
    for i in range(2, n + 1):
        res = res * i
         
    return res
 
# Function for finding number
# of K length subsequences
# whose product is even number
def countSubsequences(arr, n, k):
     
    countOdd = 0
 
    # Counting odd numbers in the array
    for i in range(n):
        if (arr[i] & 1):
            countOdd += 1;
 
    ans = nCr(n, k) - nCr(countOdd, k);
 
    return ans
     
# Driver code
arr = [ 2, 4 ]
K = 1
 
N = len(arr)
 
print(countSubsequences(arr, N, K))
 
# This code is contributed by ANKITKUAR34

// C# implementation to count of K
// length subsequence whose product
// is even
using System;
 
class GFG{
     
// Function to calculate nCr
static int nCr(int n, int r)
{
    if (r > n)
        return 0;
         
    return fact(n) / (fact(r) *
                      fact(n - r));
}
 
// Returns factorial of n
static int fact(int n)
{
    int res = 1;
    for(int i = 2; i <= n; i++)
        res = res * i;
         
    return res;
}
 
// Function for finding number
// of K length subsequences
// whose product is even number
static int countSubsequences(int []arr,
                             int n, int k)
{
    int countOdd = 0;
 
    // Counting odd numbers in the array
    for(int i = 0; i < n; i++)
    {
        if (arr[i] % 2 == 1)
            countOdd++;
    }
    int ans = nCr(n, k) - nCr(countOdd, k);
 
    return ans;
}
 
// Driver code
public static void Main(String []args)
{
    int []arr = { 2, 4 };
    int K = 1;
 
    int N = arr.Length;
 
    Console.WriteLine(countSubsequences(arr, N, K));
}
}
 
// This code is contributed by Princi Singh

<script>
 
// javascript implementation to Count of K
// length subsequence whose
// Product is even
 
 
// Function to calculate nCr
function nCr(n, r)
{
    if (r > n)
        return 0;
    return fact(n)
           / (fact(r)
              * fact(n - r));
}
 
// Returns factorial of n
function fact(n)
{
    var res = 1;
    for (var i = 2; i <= n; i++)
        res = res * i;
    return res;
}
 
// Function for finding number
// of K length subsequences
// whose product is even number
function countSubsequences( arr, n, k)
{
    var countOdd = 0;
 
    // counting odd numbers in the array
    for (var i = 0; i < n; i++) {
        if (arr[i] & 1)
            countOdd++;
    }
    var ans = nCr(n, k)
              - nCr(countOdd, k);
 
    return ans;
}
 
// Driver code
var arr = [ 2, 4 ];
var K = 1;
var N = arr.length;
document.write( countSubsequences(arr, N, K));
 
</script>

2