Recursividad finita e infinita con ejemplos

El proceso en el que una función se llama a sí misma directa o indirectamente se llama Recursión y la función correspondiente se llama función Recursiva . 
Usando Recursion, ciertos problemas se pueden resolver con bastante facilidad. Ejemplos de tales problemas son Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals , DFS , etc.

Tipos de recurrencias:

La recursividad se puede clasificar en dos tipos, dependiendo de cuándo terminan:

1. recursividad finita
2. recursividad infinita

Recursión finita:

La recursividad finita ocurre cuando la recursión termina después de un número finito de llamadas recursivas. Una recursión termina solo cuando se cumple una condición base.

Ejemplo:

A continuación se muestra una implementación para demostrar la recursividad finita.

// C++ program to demsonstrate Finite Recursion
#include <bits/stdc++.h>
using namespace std;
 
// Recursive function
void Geek(int N)
{
    // Base condition
    // When this condition is met,
    // the recursion terminates
    if (N == 0)
        return;
 
    // Print the current value of N
    cout << N << " ";
 
    // Call itself recursively
    Geek(N - 1);
}
 
// Driver code
int main()
{
 
    // Initial value of N
    int N = 5;
 
    // Call the recursive function
    Geek(N);
    return 0;
}

// Java program for the above approach
class GFG{
 
// Recursive function
static void Geek(int N)
{
     
    // Base condition
    // When this condition is met,
    // the recursion terminates
    if (N == 0)
        return;
 
    // Print the current value of N
    System.out.println(N + " ");
 
    // Call itself recursively
    Geek(N - 1);
}
 
// Driver code
public static void main(String[] args)
{
     
    // Initial value of N
    int N = 5;
 
    // Call the recursive function
    Geek(N);
}
}
 
// This code is contributed by abhinavjain194

# Python program to demsonstrate Finite Recursion
# Recursive function
def Geek( N):
 
    # Base condition
    # When this condition is met,
    # the recursion terminates
    if (N == 0):
        return
 
    # Pr the current value of N
    print( N, end =" " )
 
    # Call itself recursively
    Geek(N - 1)
 
 
# Driver code
# Initial value of N
N = 5
 
# Call the recursive function
Geek(N)
 
# this code is contributed by shivanisinghss2110

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG{
 
// Recursive function
static void Geek(int N)
{
      
    // Base condition
    // When this condition is met,
    // the recursion terminates
    if (N == 0)
        return;
  
    // Print the current value of N
    Console.Write(N + " ");
  
    // Call itself recursively
    Geek(N - 1);
}
 
// Driver Code
public static void Main(String[] args)
{
   
    // Initial value of N
    int N = 5;
  
    // Call the recursive function
    Geek(N);
}
}
 
// This code is contributed by target_2.

<script>
 
// JavaScript program to demsonstrate Finite Recursion
// Recursive function
function Geek(N)
{
    // Base condition
    // When this condition is met,
    // the recursion terminates
    if (N == 0)
        return;
 
    // Print the current value of N
    document.write(N +" ");
 
    // Call itself recursively
    Geek(N - 1);
}
 
// Driver code
// Initial value of N
    var N = 5;
 
    // Call the recursive function
    Geek(N);
     
 // this code is contributed by shivanisinghss2110
  
</script>

5 4 3 2 1 

El árbol de recursividad para la función recursiva anterior se ve así.

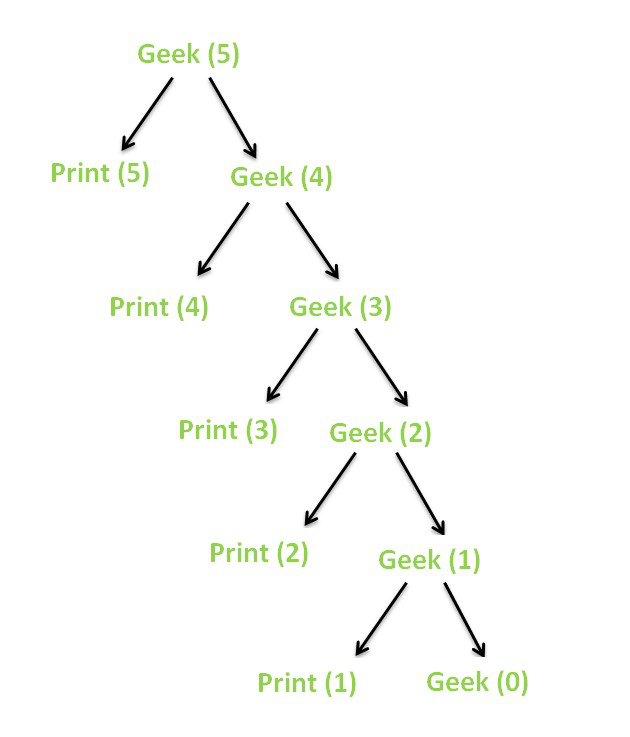
Árbol de recursión

Cuando el valor de N se convierte en 0 , debido a la condición base, la recursividad termina.

Recursividad infinita:

La recursividad infinita ocurre cuando la recursividad no termina después de un número finito de llamadas recursivas. Como nunca se cumple la condición base, la recursividad continúa infinitamente.

Ejemplo: 

A continuación se muestra una implementación para demostrar la recursividad infinita. 

// C++ program to demsonstrate Infinite Recursion
#include <bits/stdc++.h>
using namespace std;
 
// Recursive function
void Geek(int N)
{
    // Base condition
    // This condition is never met here
    if (N == 0)
        return;
 
    // Print the current value of N
    cout << N << " ";
 
    // Call itself recursively
    Geek(N);
}
 
// Driver code
int main()
{
 
    // Initial value of N
    int N = 5;
 
    // Call the recursive function
    Geek(N);
    return 0;
}

// Java program to demsonstrate Infinite Recursion
import java.io.*;
  
class GFG
{
// Recursive function
static void Geek(int N)
{
    // Base condition
    // This condition is never met here
    if (N == 0)
        return;
 
    // Print the current value of N
    System.out.print( N +" ");
 
    // Call itself recursively
    Geek(N);
}
 
// Driver code
public static void main(String[] args)
    {
 
    // Initial value of N
    int N = 5;
 
    // Call the recursive function
    Geek(N);
    }
}
 
// This code is contributed by shivanisinghss2110

# Python3 to demsonstrate Infinite Recursion
 
# Recursive function
def Geek(N):
     
    # Base condition
    # This condition is never met here
    if (N == 0):
        return
 
    # Print the current value of N
    print(N, end = " " )
 
    # Call itself recursively
    Geek(N)
 
# Driver code
 
# Initial value of N
N = 5
 
# Call the recursive function
Geek(N)
 
# This code is contributed by shivanisinghss2110

// C# program to demsonstrate Infinite Recursion
using System;
  
class GFG
{
// Recursive function
static void Geek(int N)
{
    // Base condition
    // This condition is never met here
    if (N == 0)
        return;
 
    // Print the current value of N
    Console.Write( N +" ");
 
    // Call itself recursively
    Geek(N);
}
 
// Driver code
public static void Main(String[] args)
    {
 
    // Initial value of N
    int N = 5;
 
    // Call the recursive function
    Geek(N);
    }
}
 
// This code is contributed by shivanisinghss2110

<script>
// JavaScript program to demsonstrate Infinite Recursion
// Recursive function
function Geek(N)
{
    // Base condition
    // This condition is never met here
    if (N == 0)
        return;
 
    // Print the current value of N
    document.write( N +" ");
 
    // Call itself recursively
    Geek(N);
}
 
// Driver code
    // Initial value of N
    var N = 5;
 
    // Call the recursive function
    Geek(N);
 
// This code is contributed by shivanisinghss2110
</script>

El árbol de recursividad para la función recursiva anterior se ve así.

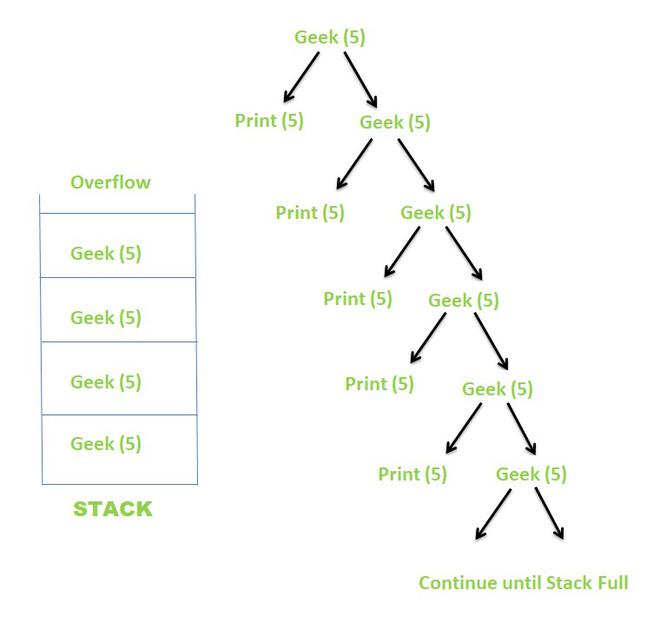
Árbol de recursión

Dado que el valor de N nunca se convierte en 0 , la recursividad nunca termina. En cambio, la recursividad continúa hasta que la pila implícita se llena, lo que da como resultado un desbordamiento de pila . Algunos compiladores dan directamente la salida como falla de segmentación (núcleo volcado) , mientras que otros pueden terminar anormalmente por algún valor y luego mostrar la falla de segmentación .