Ray Optics es una rama de la óptica que describe la propagación de la luz en forma de rayos. Ray Optics también se llama óptica geométrica y se ocupa de la geometría de las luces que caen. este artículo trata sobre la refracción, sus leyes, la refracción a través de la losa de vidrio y sus diversas causas, y la práctica de trazar el camino de los rayos de luz que pasan a través de la losa de vidrio. La refracción es la propiedad del cambio de dirección de la onda al pasar de un medio a otro medio. Este cambio de dirección se debe a un cambio en la velocidad de la onda.
¿Qué es la refracción?
La refracción es el fenómeno del cambio en la dirección de una onda que pasa de un medio a otro medio debido al cambio en su velocidad. La refracción se refiere a la flexión de una onda cuando pasa de un medio a otro medio.
La onda se dobla debido al cambio en su velocidad de un medio a otro medio. Aquí hay dos leyes de la refracción que se pueden establecer como:
- El rayo incidente, el rayo refractado y la normal en un punto de incidencia se encuentran en el mismo plano.
- La relación entre el seno del ángulo de incidencia y el seno del ángulo de refracción es constante. Esto se conoce como Ley de refracción de Snell.
sen i / sen r = constante
¿Qué es la losa de vidrio?
Una losa de vidrio es una sustancia con forma de paralelepípedo que está hecha de vidrio. Una losa de vidrio está hecha de vidrio con tres dimensiones de largo, ancho y alto.

Algunas propiedades importantes de una losa de vidrio se pueden establecer como:
- La losa de vidrio no se desvía de los rayos de luz que la atraviesan.
- La losa de vidrio no dispersa los rayos de luz que la atraviesan.
- Dado que no se desvía ni dispersa los rayos de luz que lo atraviesan, es por eso que el rayo incidente y el rayo emergente que emerge de la losa de vidrio son paralelos. La losa de vidrio solo produce un desplazamiento lateral en la dirección de la luz.
Refracción a través de la losa de vidrio
- Cuando el rayo incidente incide sobre la superficie de la losa de vidrio desde el aire hasta el vidrio formando un ángulo de incidencia i con la normal, el rayo refractado se dobla hacia la normal a medida que el rayo ingresa del medio más raro al más denso.

Refracción a través de la losa de vidrio
- Ahora, después de viajar por la losa de vidrio, el rayo refractado forma un ángulo de incidencia r en la otra superficie de la losa de vidrio, lo que da como resultado que el rayo emergente se desvíe de la normal a medida que viaja del vidrio (medio más denso) al aire (medio más raro) formando un ángulo de emergencia e entre el rayo emergente y la normal.
- El rayo emergente es paralelo al rayo incidente y la distancia perpendicular entre ellos se llama desplazamiento lateral.
- Dado que el ángulo de incidencia es igual al ángulo de emergencia, el rayo emergente es paralelo al rayo incidente.
- En la losa de vidrio, el rayo de luz se refracta dos veces, primero, del medio más raro al más denso y, en segundo lugar, del medio más denso al más raro. El desplazamiento creado en el rayo emergente se debe a la refracción.
Por lo tanto, la fórmula para el desplazamiento lateral d está dada por,
d = [t sin(i – r)]/ cos r = t sin(i – r) sec r
donde t es el espesor de la losa de vidrio, i es el ángulo de incidencia, r es el ángulo de refracción.
Experimento para trazar la trayectoria de un rayo de luz que pasa a través de una losa de vidrio
Objetivo: Trazar la trayectoria de un rayo de luz que pasa a través de la losa de vidrio.
Materiales necesarios: tablero de dibujo, todos los alfileres, papel blanco, losa de vidrio rectangular, transportador, escala, lápiz, alfileres.
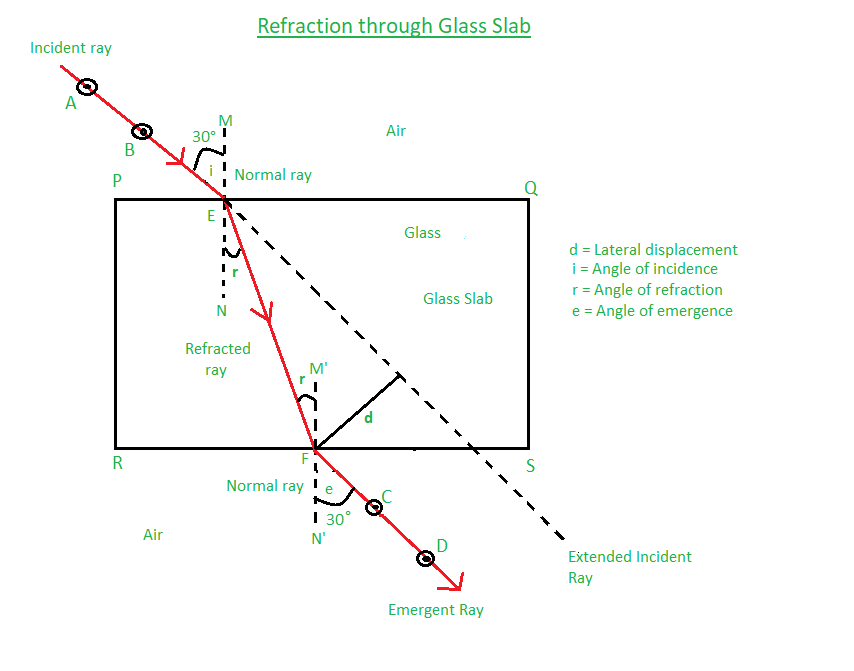
Trazar la trayectoria de un rayo de luz que pasa a través de una losa de vidrio
Procedimiento:
- Fije el papel blanco en el tablero de dibujo con la ayuda de alfileres.
- Coloque la losa de vidrio en el centro del papel y dibuje un contorno de la losa de vidrio y etiquételo como PQRS.
- Dibuje un punto E en PQ y dibuje la perpendicular MN y etiquételo como un rayo normal.
- Dibuja un ángulo de 30° con un transportador con MN. Fije los pines A y B, separados 4-5 cm uno del otro en el rayo que se obtiene por el ángulo formado.
- Coloque la losa de vidrio en el contorno PQRS y mire a través de la losa de vidrio desde el lado RS y fije los pasadores C y D de modo que A, B, C y D queden en la misma línea.
- Dibuja pequeños círculos en A, B, C y D y quita los alfileres.
- Una C, D de modo que se crucen en el punto F en RS y dibuje la perpendicular M’N’ en el punto F.
- Ahora, une los puntos E y F.
- Mida los ángulos formados en PQ y RS, que son el ángulo de incidencia, el ángulo de refracción y el ángulo de emergencia.
- El desplazamiento lateral d se obtiene extendiendo el rayo AB en la línea punteada paralelo a FCD y luego midiéndolo.
Conclusión:
- El ángulo de incidencia es casi igual al ángulo de emergencia.
- A medida que la luz viaja de un medio más raro a uno más denso, el ángulo de refracción será menor que el ángulo de refracción.
- Para diferentes ángulos de incidencia, el desplazamiento lateral será el mismo.
- La luz se desvía hacia lo normal cuando viaja de un medio más raro a uno más denso.
Diferentes casos de refracción a través de placa de vidrio
Caso 1: Refracción cuando el objeto está en un medio más denso y el observador está en un medio más raro
Considere una losa de vidrio con índice de refracción y espesor μ y t respectivamente. El observador (ojo) está en el aire y el objeto (O) está en la losa de vidrio.

Refracción cuando el objeto está en un medio más denso y el observador está en un medio más raro
Por lo tanto, para este caso,
Profundidad virtual = t / μ
y
Desplazamiento virtual (OI) = OA – AI = t[1-(1/ μ)]
Caso 2: Refracción a través de losas sucesivas con diferentes espesores e índice de refracción
Considere tres losas sucesivas s 1 , s 2 y s 3 con espesor t 1 , t 2 , t 3 e índices de refracción μ 1 , μ 2 y μ 3 respectivamente. Estas losas están dispuestas una tras otra con s 1 en la parte superior, s 2 en el medio y s 3 en la parte inferior. El objeto (O) está en s 3 y el observador (ojo) está afuera en el aire (medio más raro).

Refracción a través de losas sucesivas con diferentes espesores e índice de refracción
Por lo tanto, para este caso,
Profundidad virtual (AI) = (t 1 / μ 1 ) + (t 2 / μ 2 ) + (t 3 / μ 3 ) + …….
y
Desplazamiento virtual (OI) = t 1 [1 – (1/ μ 1 )] + t 2 [1 – (1/ μ 2 )] + t 3 [1 – (1/ μ 3 )] + ………
Caso 3: Refracción cuando el objeto y el observador están en un medio más raro
Considere una losa de vidrio con espesor t e índice de refracción μ. En este caso, el objeto (O) y el observador (ojo) están en un medio más raro (aire) separados por la losa de vidrio.

Refracción cuando el objeto y el observador están en un medio más raro
Por lo tanto, para este caso,
Desplazamiento virtual (OI) = [t – (1/ μ)]
Caso 4: Refracción cuando el objeto está en un medio más raro y el observador está en un medio más denso
Considere que el observador (ojo) está en el agua (medio más denso) y el objeto (O) está en el aire (medio más raro).

Refracción cuando el objeto está en un medio más raro y el observador está en un medio más denso
Por lo tanto, para este caso,
Altura real / Altura virtual = 1 / μ
o
Desplazamiento virtual (OI) = AI – AO = (μ – 1)AO
Ejemplos de preguntas
Pregunta 1: Determine la posición del objeto que se encuentra en la parte inferior de la losa de vidrio con un espesor de 12 cm y el índice de refracción del vidrio es de 1,5.
Responder:
El caso dado es la refracción cuando el objeto está en un medio más denso y el observador está en el medio más raro.
Tenemos que encontrar la profundidad virtual, es decir, la posición del objeto.
Aquí, t = 12 cm y μ = 1,5
Posición del objeto = t / μ
= 12/1,5
= 120/15
Posición del objeto = 8 cm
Pregunta 2: Dos líquidos inmiscibles de índices de refracción 3/2 y 4/3 llenan el recipiente hasta 9 cm y 12 cm entonces, ¿Cuál será la profundidad virtual del fondo del recipiente?
Responder:
El caso dado es como la refracción a través de placas sucesivas con diferente espesor e índice de refracción.
Aquí, t 1 = 9 cm, μ 1 = 3/2, t 2 = 12 cm y μ 2 = 4/3
Profundidad virtual = (t 1 /μ 1 ) + (t 2 /μ 2 )
= (9/(3/2)) + (12/(4/3))
= (18/3) + (36/4)
= 6 + 9
Profundidad virtual = 15 cm
Pregunta 3: Se mantiene un objeto en el fondo del recipiente vacío y se enfoca un microscopio para observarlo. Ahora, se llena de agua hasta 16 cm, entonces, a qué cantidad debe moverse el microscopio para que pueda enfocar nuevamente el objeto. El índice de refracción es 4/3.
Responder:
El caso dado es la refracción cuando el objeto está en un medio más denso y el observador está en el medio más raro.
Aquí, t = 16 cm, μ = 4/3
El microscopio de cantidad debe moverse para que pueda enfocar nuevamente el objeto = Desplazamiento virtual = t[1- (1/μ)]
= 16[1 – {1/(4/3)}]
= 16 [1 – 3/4]
= 16 × (1/4)
La cantidad de microscopio debe moverse para que pueda enfocar nuevamente el objeto = 4 cm.
Pregunta 4: Una burbuja de aire en una losa de vidrio (μ = 1.5) tiene 5 cm de profundidad cuando se ve desde una cara y 2 cm de profundidad cuando se ve desde la cara opuesta, luego encuentre el grosor de la losa.
Responder:
Dado:
µ = 1,5
Profundidad virtual v 1 cuando se observa desde una cara = 5 cm
Profundidad virtual v 2 cuando se observa desde la cara opuesta = 2 cm
Tenemos que encontrar la profundidad real. Este caso es cuando el objeto está en un medio más denso y el observador está en el medio más raro.
Cuando se observa desde una cara:
v 1 = r 1 /μ
r 1 = v 1 × μ
= 5 × 1,5 = 7,5 cm
Cuando se observa desde la cara opuesta:
v 2 = r 2 /μ
r 2 = v 2 × μ
= 2 × 1,5 = 3,0 cm
Espesor de la placa de vidrio = r 1 + r 2 = 7,5 + 3,0
= 10,5 cm
Pregunta 5: ¿Qué es el desplazamiento lateral? Indique los factores de los que depende.
Responder:
La distancia perpendicular entre el rayo incidente y el rayo emergente resultante se denomina desplazamiento lateral.
Factores de los que depende el desplazamiento lateral:
- El espesor de la losa de vidrio.
- Ángulo de incidencia
- índice de refracción del vidrio
- La longitud de onda de la luz utilizada
Pregunta 6: ¿Por qué el rayo emergente es paralelo al rayo incidente en la refracción a través de la losa de vidrio?
Responder:
El rayo emergente es paralelo al rayo incidente en la refracción a través de la losa de vidrio porque el ángulo de incidencia y el ángulo de refracción son iguales.
Pregunta 7: Encuentre el desplazamiento lateral cuando se produce la refracción a través de una losa de vidrio donde el ángulo de incidencia es de 45° y el ángulo de refracción es de 30° y el espesor de la losa de vidrio es de 10 cm.
Responder:
Aquí, t = 10 cm, i = 45°, r = 30°
Desplazamiento lateral (d) = [t sin(i – r)]/ cos r
= [10 sen( 45° – 30°)]/ cos 30°
= [10 sen 15°]/ cos 30°
= 10 × (sen 15° / cos 30°)
= 10 × (0,25/0,86)
= 10 × 0,29
Desplazamiento lateral (d) = 2,9 cm
Publicación traducida automáticamente
Artículo escrito por aayushi2402 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA