Regla de Cramer

Las arrays son uno de los temas importantes en matemáticas. Las arrays y los determinantes se utilizan para encontrar las soluciones a diferentes sistemas de ecuaciones. La regla de Cramer se usa para encontrar las incógnitas en el sistema dado de ecuaciones lineales. Veamos cómo aplicar la regla de Cramer y su explicación. Requiere un conocimiento previo de arrays, determinantes y el sistema de ecuaciones lineales.

La regla de Cramer es una regla que se usa para encontrar las incógnitas del conjunto dado de ecuaciones lineales. Esta regla es válida solo si el sistema de ecuaciones dado tiene una solución única. No funciona con el sistema de ecuaciones con infinitas soluciones o sin solución. Esta regla se usa para encontrar soluciones para cualquier número de variables con el mismo número de ecuaciones. Esta regla usa determinantes para encontrar la solución de las ecuaciones dadas o el valor de las incógnitas.

Fórmula de la regla de Cramer

La fórmula de la regla de Cramer para resolver el sistema AX = B (donde, A= array de coeficientes, B = array de columna de constantes (RHS), X = array de columna de incógnitas) o para encontrar los valores de las variables involucra los siguientes pasos,

Pasos de la fórmula de la regla de Cramer

Escribe el sistema de ecuaciones dado en forma AX = B.
Encuentre el valor del determinante ( D ) de la array A. ( Nota: si el determinante es cero, entonces un sistema de ecuaciones no tiene una solución única, lo cual no es válido en la regla de Cramer).
Ahora, encuentre el valor D _x que es el determinante de la array A en la que las constantes de las ecuaciones lineales dadas reemplazan el coeficiente de x.
Ahora, encuentre el valor D _y que es el determinante de la array A en la que el coeficiente de y se reemplaza por las constantes de las ecuaciones lineales dadas.
Ahora, encuentre el valor D _z que es el determinante de la array A en la que el coeficiente de z se reemplaza por las constantes de las ecuaciones lineales dadas. (Encuentre este determinante solo si hay 3 variables presentes en la ecuación dada).
De manera similar, encuentre determinantes para todas las incógnitas si hay más de tres incógnitas presentes.
Encuentre los valores de x = D _x /D , y = D _y /D , z = D _z /D.

Ejemplos de preguntas

Pregunta 1: Resuelve: 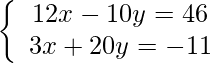$\left\{ \begin{array}{c} 12x-10y= 46\\ 3x+20y=-11 \\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 12 & -10 \\ 3 & 20 \end{bmatrix}$ , B = $\begin{bmatrix} 46 \\ -11 \end{bmatrix}$ , X = $\begin{bmatrix} x \\ y \end{bmatrix}$

Entonces, el determinante D de la array A = $\begin{vmatrix} 12 & -10 \\ 3 & 20 \\ \end{vmatrix}$ = 12 × 20 – 3 × (-10) = 240 + 30 = 270

Ahora, encuentre D _x y D _y

re _x = $\begin{vmatrix} 46 & -10 \\ -11& 20 \\ \end{vmatrix}$ = [46×20 – (-10)×(-11)] = 920 – 110 = 810

D _y = $\begin{vmatrix} 12 & 46 \\ 3 & -11 \\ \end{vmatrix}$ =[12×(-11) – 3×46] = -132 -138 = -270

Ahora, encuentre x = D _x /D, y = D _y /D

x = 810/270 = 3, y = -270/270 = -1

x = 3, y = -1

Pregunta 2: Resuelve: 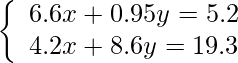$\left\{ \begin{array}{c} 6.6x+0.95y= 5.2\\ 4.2x+8.6y=19.3 \\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 6.6& 0.95 \\ 4.2& 8.6 \\ \end{bmatrix}$ , B = $\begin{bmatrix} 5.2 \\ 19.3 \end{bmatrix}$ , X = $\begin{bmatrix} x \\ y \end{bmatrix}$

Entonces, el determinante D de la array A = $\begin{vmatrix} 6.6& 0.95 \\ 4.2& 8.6 \\ \end{vmatrix}$ = 6,6×8,6 – 4,2×0,95 = 56,76 – 3,99 =52,77

Ahora, encuentre D _x y D _y

D _x = $\begin{vmatrix} 5.2& 0.95 \\ 19.3& 8.6 \\ \end{vmatrix}$ = 5,2 × 8,6 – 19,3 × 0,95 = 44,72 – 18,335 = 26,385

D _y = $\begin{vmatrix} 6.6& 5.2 \\ 4.2& 19.3 \\ \end{vmatrix}$ = 6,6×19,3 – 4,2×5,2 = 127,38 – 21,84 = 105,54

Ahora, encuentra x = D _x /D , y = D _y /D

x = 26,385/52,77 = 0,5, y = 105,54/52,77 = 2

x = 0,5, y = 2

Pregunta 3: Resuelve: $\left\{ \begin{array}{c} 3x^2+4y^2= 91\\ 6x^2-y^2=38 \\ \end{array} \right.$

Solución:

Sea x ² = a, y ² = b

Entonces, la ecuación se puede escribir como:

$\left\{ \begin{array}{c} 3a+4b= 91\\ 6a-b=38 \\ \end{array} \right.$

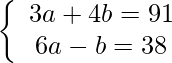
Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 3& 4 \\ 6&-1 \\ \end{bmatrix}$ , B = $\begin{bmatrix} 91 \\ 38 \end{bmatrix}$ , X = $\begin{bmatrix} a \\ b \end{bmatrix}$

Entonces, el determinante D de la array A = $\begin{vmatrix} 3& 4 \\ 6& -1 \end{vmatrix}$ = 3×(-1) – 6×4 = -3-24 = -27

Ahora, encuentra D _a y D _b

re ₌ = $\begin{vmatrix} 91& 4 \\ 38& -1 \end{vmatrix}$ 91×(-1) – 38×4 = – 91 – 152 = -243

re _segundo = $\begin{vmatrix} 3& 91 \\ 6& 38 \end{vmatrix}$ = 3×38 – 6×91 = 114 – 546 = -432

Ahora, encuentra a = D _a /D, b = D _b /D

a = -243/-27 = 9, b = -432/-27 = 16

a = 9, b = 16

Ahora x ² = a = 9, x = √9 = 3

y ² = segundo = 16, y = √16 = 4

Pregunta 4: Resuelve: 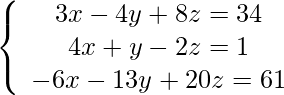$\left\{ \begin{array}{c} 3x-4y+8z= 34\\ 4x+y-2z=1\\ -6x-13y+20z=61\\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 3& -4& 8 \\ 4&1&-2 \\-6&-13&20 \end{bmatrix}$ , B = $\begin{bmatrix} 34 \\ 1 \\ 61 \end{bmatrix}$ , X = $\begin{bmatrix} x \\ y \\ z \end{bmatrix}$

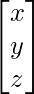
Entonces, el determinante D de la array A = $\begin{vmatrix} 3& -4& 8 \\ 4&1&-2 \\-6&-13&20 \end{vmatrix}$ = 3(20 – 26) – (-4)(80 – 12) + 8(-52-(-6)) = 3×(-6) + 4×68 – 46 ×8 = -18 + 272 – 368

= -114

Ahora, encuentre D _x , D _y y D _z

RE _x = $\begin{vmatrix} 34& -4& 8 \\ 1&1&-2 \\61&-13&20 \end{vmatrix}$ = 34(20 – 26) – (-4)(20 + 122) + 8(-13 – 61)

= 34 × (-6) + 4 × 142 + 8 × (-74) = -204 + 568 – 592 = -228

D _y = $\begin{vmatrix} 3& 34& 8 \\ 4&1&-2 \\-6&61&20 \end{vmatrix}$ = 3(20 + 2 × 61) – 34(80 – 12) + 8(61 × 4 + 6)

= 3 × 142 – 34 × 68 + 8 × 250 = 426 – 2312 + 2000 = 114

re _z = $\begin{vmatrix} 3& -4& 34 \\ 4&1&1 \\-6&-13&61 \end{vmatrix}$ = 3(61+13) – (-4)(61×4 + 6) + 34(-52+6)

= 3 × 74 + 4 × 250 + 34 × (-46) = 222 + 1000 -1564 = -342

Ahora, encuentra x = D _x /D, y = D _y /D, z = D _z /D

x = -228/-114 = 2, y = 114/-114 = -1, z = -342/-114 = 3

x = 2, y = -1, z = 3

Pregunta 5: Resuelve: 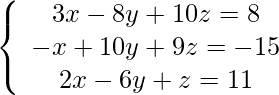$\left\{ \begin{array}{c} 3x-8y+10z= 8\\ -x+10y+9z=-15\\ 2x-6y+z=11\\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 3& -8& 10 \\ -1&10&9 \\2&-6&1 \end{bmatrix}$ , B = $\begin{bmatrix} 8 \\ -15 \\ 11 \end{bmatrix}$ , X = $\begin{bmatrix} x \\ y \\ z \end{bmatrix}$

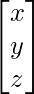
Entonces, el determinante D de la array A = $\begin{vmatrix} 3& -8& 10 \\ -1&10&9 \\2&-6&1 \end{vmatrix}$ = 3(10+54) + 8(-1-18) +10(6-20)

= 3 × 64 – 8 × 19 + 10 × (-14) = 192 -152 – 140 = -100

Ahora, encuentre D _x , D _y y D _z

RE _x = $\begin{vmatrix} 8& -8& 10 \\ -15&10&9 \\11&-6&1 \end{vmatrix}$ = 8(10+54) + 8(-15-99) + 10(90 -110)

= 8 × 64 + 8 × (-114) + 10 × (-20) = 512 – 912 – 200 = -600

D _y = $\begin{vmatrix} 3& 8& 10 \\ -1&-15&9 \\2&11&1 \end{vmatrix}$ = 3(-15-99) – 8(-1-18) + 10(-11+30)

= 3 × (-114) + 8 × 19 + 10 × 19 = -342 + 152 +190 = 0

re _z = $\begin{vmatrix} 3& -8& 8 \\ -1&10&-15 \\2&-6&11 \end{vmatrix}$ = 3(110-90) + 8(-11+30) + 8(6-20)

= 3 × 20 + 8 × 19 + 8 × (-14) = 60 + 152 – 112 = 100

Ahora, encuentra x = D _x /D, y = D _y /D, z = D _z /D

x = -600/-100 = 6, y = 0/-100 = 0, z = 100/-100 = -1

x = 6, y = 0, z = -1

Pregunta 6: Resuelve: 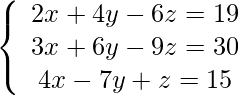$\left\{ \begin{array}{c} 2x+4y-6z= 19\\ 3x+6y-9z=30\\ 4x-7y+z=15\\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = , B = , X = $\begin{bmatrix} 2& 4& -6 \\ 3&6&-9 \\4&-7&1 \end{bmatrix}$ $\begin{bmatrix} 19 \\ 30 \\ 15 \end{bmatrix}$ $\begin{bmatrix} x \\ y \\ z \end{bmatrix}$

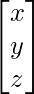
Entonces, el determinante D de la array A = = 2(6 – 63) – 4(3 + 36) – 6(-21 – 24) = 2 × (-57) – 4 × 39 – 6 × (-45) = -114 – 156 + 270 = 0

Desde |D| = 0, lo que significa que el sistema de ecuaciones dado no tiene una solución única, lo cual no es válido en la regla de Cramer, ya que se define solo para el sistema de ecuaciones que tiene una solución única. Esto significa que el sistema de ecuaciones dado tiene solución infinita o no tiene solución.

Pregunta 7: Resuelve: 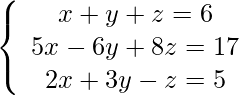$\left\{ \begin{array}{c} x+y+z= 6\\ 5x-6y+8z=17\\ 2x+3y-z=5\\ \end{array} \right.$

Solución:

Las ecuaciones dadas en forma de AX = B

A = $\begin{bmatrix} 1& 1& 1 \\ 5&-6&8 \\2&3&-1 \end{bmatrix}$ , B = $\begin{bmatrix} 6 \\ 17 \\ 5 \end{bmatrix}$ , X = $\begin{bmatrix} x \\ y \\ z \end{bmatrix}$

Entonces, el determinante D de la array A = $\begin{vmatrix} 1& 1& 1 \\ 5&-6&8 \\2&3&-1 \end{vmatrix}$ = 1(6 – 24) – 1(-5 – 16) + 1(15 + 12)

= -18 + 21 + 27 = 30

Ahora, encuentre D _x , D _y y D _z

Dx = = 6(6-24) -1(-17-40) +1( ₅₁ $\begin{vmatrix} 6& 1& 1 \\ 17&-6&8 \\5&3&-1 \end{vmatrix}$ +30)

= 6(-18) + 57 + 81 = -108 + 138 = 30

D _y = $\begin{vmatrix} 1& 6& 1 \\ 5&17&8 \\2&5&-1 \end{vmatrix}$ = 1(-17 – 40) – 6(-5 – 16) + 1(25 – 34) = -57 + 126 – 9 = 60

D _z = $\begin{vmatrix} 1& 1& 6 \\ 5&-6&17 \\2&3&5 \end{vmatrix}$ = 1(-30 – 51) – 1(25 – 34) + 6(15 + 12) = -81 + 9 + 162 = 90

Ahora, encuentra x = D _x /D, y = D _y /D, z = D _z /D

x = 30/30 = 1, y = 60/30 = 2, z = 90/30 = 3

x = 1, y = 2, z = 3