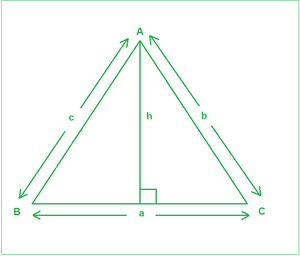
Dados los ángulos (en grados) A , C y el lado c , correspondientes a la figura de abajo, la tarea es encontrar los dos lados restantes a y b .
Ejemplos:
Entrada: A = 45, C = 35, c = 23
Salida:
28,35
39,49
Explicación:
a es 28,35 y b es 39,49Entrada: A = 45, C = 45, c = 10
Salida:
10
14.14
Enfoque: La idea es usar la regla del seno . Establece que los lados de cualquier triángulo son proporcionales al seno de los ángulos opuestos a ellos. a / Sin(A) = b / Sin(B) = c / Sin(C) . La derivación se describe a continuación:
Como se desprende de la figura anterior:
Se ha trazado una perpendicular de longitud h en BC desde A . De las reglas trigonométricas generales:
SenB=h/c——–(1)
SinC=h/b——–(2)
De las dos ecuaciones anteriores, obtenemos:
cx SinB=bx SinC
o b/SenB=c/SenC—–(3)
De manera similar, si se traza una perpendicular de B a AC , podemos obtener:
a/SenA=c/SenC——-(4)
De las ecuaciones (3) y (4) obtenemos:
a/SenA=b/SenB=c/SenC
Siga los pasos a continuación para resolver el problema:
- Cambie los ángulos A y C de grados a radianes para poder usarlos en las funciones incorporadas.
- Calcula el ángulo B usando la observación de que las sumas de los ángulos de un triángulo suman 180 grados.
- Usa la regla del seno para calcular los lados a y b .
A continuación se muestra la implementación del enfoque anterior:
C++14
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to calculate remaining two sides
void findSides(double A, double C, double c)
{
// Calculate angle B
double B = 180 - (A + C);
// Convert angles to their respective radians for
// using trigonometric functions
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
// Sine rule
double a = (c / sin(C)) * sin(A);
double b = (c / sin(C)) * sin(B);
// Precision of 2 decimal spaces
cout << fixed << setprecision(2);
// Print the answer
cout << a << endl;
cout << b << endl;
}
// Driver Code
int main()
{
// Input
double A = 45.0;
double C = 35.0;
double c = 23;
// Function Call
findSides(A, C, c);
return 0;
}
Java
// Java program for the above approach
class GFG{
// Function to calculate remaining two sides
static void findSides(double A, double C,
double c)
{
// Calculate angle B
double B = 180 - (A + C);
// Convert angles to their respective
// radians for using trigonometric functions
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
// Sine rule
double a = (c / Math.sin(C)) * Math.sin(A);
double b = (c / Math.sin(C)) * Math.sin(B);
// Print the answer
System.out.println(String.format("%.2f", a));
System.out.println(String.format("%.2f", b));
}
// Driver code
public static void main(String[] args)
{
// Input
double A = 45.0;
double C = 35.0;
double c = 23;
// Function Call
findSides(A, C, c);
}
}
// This code is contributed by abhinavjain194
Python3
# Python3 program for the above approach
import math
# Function to calculate remaining two sides
def findSides(A, C, c):
# Calculate angle B
B = 180 - (A + C)
# Convert angles to their respective radians
# for using trigonometric functions
A = A * (3.14159 / 180)
C = C * (3.14159 / 180)
B = B * (3.14159 / 180)
# Sine rule
a = (c / math.sin(C)) * math.sin(A)
b = (c / math.sin(C)) * math.sin(B)
# Precision of 2 decimal spaces
# Print the answer
print("{0:.2f}".format(a))
print("{0:.2f}".format(b))
# Driver Code
# Input
A = 45.0
C = 35.0
c = 23
# Function Call
findSides(A, C, c)
# This code is contributed by target_2
C#
// C# program for the above approach
using System;
class GFG{
// Function to calculate remaining two sides
static void findSides(double A, double C,
double c)
{
// Calculate angle B
double B = 180 - (A + C);
// Convert angles to their respective
// radians for using trigonometric functions
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
// Sine rule
double a = (c / Math.Sin(C)) * Math.Sin(A);
double b = (c / Math.Sin(C)) * Math.Sin(B);
// Print the answer
Console.WriteLine("{0:F2}",a);
Console.WriteLine("{0:F2}",b);
}
// Driver code
public static void Main(String[] args)
{
// Input
double A = 45.0;
double C = 35.0;
double c = 23;
// Function Call
findSides(A, C, c);
}
}
// This code is contributed by shivanisinghss2110
Javascript
<script>
// JavaScript program for the above approach
// Function to calculate remaining two sides
function findSides(A, C, c)
{
// Calculate angle B
let B = 180 - (A + C);
// Convert angles to their respective radians for
// using trigonometric functions
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
// Sine rule
let a = (c / Math.sin(C)) * Math.sin(A);
let b = (c / Math.sin(C)) * Math.sin(B);
// Precision of 2 decimal spaces
// Print the answer
document.write(a.toPrecision(4) + "<br>");
document.write(b.toPrecision(4) + "<br>");
}
// Driver Code
// Input
let A = 45.0;
let C = 35.0;
let c = 23;
// Function Call
findSides(A, C, c);
// This code is contributed by Potta Lokesh
</script>
28.35 39.49
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)