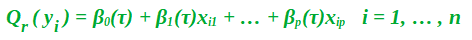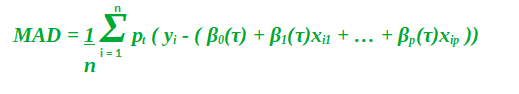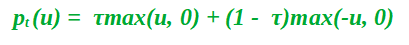La regresión cuantil es un algoritmo que estudia el impacto de las variables independientes en diferentes cuantiles de la distribución de la variable dependiente. La regresión de cuantiles proporciona una imagen completa de la relación entre Z e Y. Es robusta y eficaz para los valores atípicos en las observaciones de Z. En la regresión por cuantiles, la estimación y las inferencias no tienen distribución. La regresión por cuantiles es una extensión de la regresión lineal, es decir, cuando no se cumplen las condiciones de la regresión lineal (es decir, linealidad, independencia o normalidad), se utiliza . Estima la función cuantil condicional como una combinación lineal de los predictores, utilizada para estudiar las relaciones de distribución de las variables, ayuda a detectar la heteroscedasticidad, y también útil para tratar con variables censuradas. Es muy fácil realizar una regresión de cuantiles en la programación R.
Expresión Matemática
La regresión por cuantiles es más efectiva y robusta para los valores atípicos. En la regresión por cuantiles, no está limitado a encontrar la mediana, es decir, puede calcular cualquier porcentaje (cuantil) para un valor particular en las variables de características. Por ejemplo, si uno quiere encontrar el cuantil 30 del precio de un edificio en particular, eso significa que hay un 30 % de probabilidad de que el precio real del edificio esté por debajo de la predicción, mientras que hay un 70 % de probabilidad de que el precio está arriba. Por lo tanto, la ecuación del modelo de regresión por cuantiles es:
Entonces, ahora en lugar de ser constantes, los coeficientes beta ahora han funcionado con una dependencia en el cuantil. Encontrar los valores para estas betas en un valor de cuantil particular tiene casi el mismo proceso que para la cuantificación lineal regular. Ahora tenemos que reducir la desviación absoluta mediana.
Además, matemáticamente p t toma la forma:
La función p t (u) es la función de verificación que otorga pesos asimétricos al error que depende del cuantil y el signo general del error.
Implementación en R
El conjunto de datos:
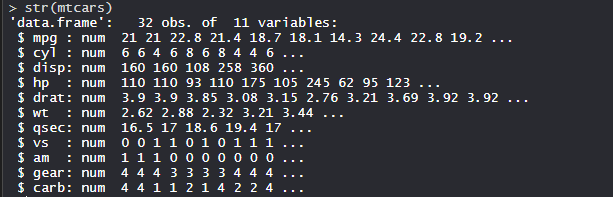
mtcars (prueba de carretera de automóviles de tendencia del motor) comprende el consumo de combustible, el rendimiento y 10 aspectos del diseño del automóvil para 32 automóviles. Viene preinstalado con el paquete dplyr en R.
R
# Installing the package
install.packages("dplyr")
# Loading package
library(dplyr)
# Structure of dataset in package
str(mtcars)
Producción:
Realización de una regresión cuantil en un conjunto de datos:
Usar el algoritmo de regresión cuantil en el conjunto de datos entrenando el modelo usando características o variables en el conjunto de datos.
R
# Installing Packages
install.packages("quantreg")
install.packages("ggplot2")
install.packages("caret")
# Loading the packages
library(quantreg)
library(dplyr)
library(ggplot2)
library(caret)
# Model: Quantile Regression
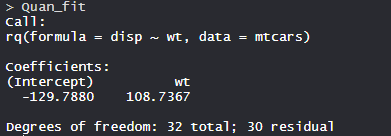
Quan_fit <- rq(disp ~ wt, data = mtcars)
Quan_fit
# Summary of Model
summary(Quan_fit)
# Plot
plot(disp ~ wt, data = mtcars, pch = 16, main = "Plot")
abline(lm(disp ~ wt, data = mtcars), col = "red", lty = 2)
abline(rq(disp ~ wt, data = mtcars), col = "blue", lty = 2)
Producción:
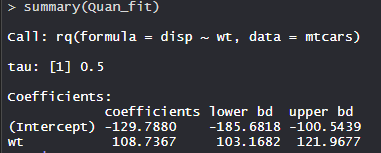
- Modelo Quan_fit:
El modelo Quan_fit tiene Intercepción -129.7880 con 32 Grados de Libertad.
- Resumen Modelo:
El modelo tiene un valor tau de 0,5 con bd inferior es -185,6818 y bd superior es -100,5439 de coeficiente -129,7880.
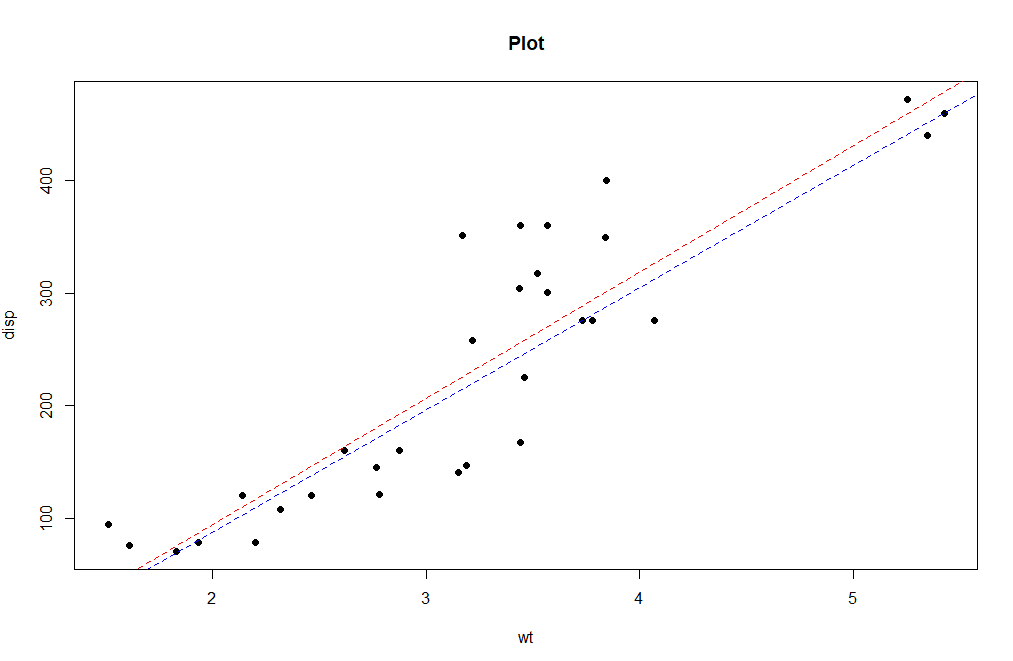
- Gráfico:
El gráfico muestra la línea de regresión del cuantil en azul y la línea de regresión lineal en rojo. Por lo tanto, las aplicaciones de regresión de Quantile se utilizan en gráficos de crecimiento, estadísticas, análisis de regresión con capacidad total.
Ventajas de la regresión cuantil
- Ayuda a comprender la relación entre variables de datos que tienen relaciones no lineales con variables predictoras.
- Es robusto y efectivo para valores atípicos .
- Ayuda a obtener una dispersión estadística que ayuda a una revisión más profunda entre la relación de las variables.