Los datos univariados son el tipo de datos en los que el resultado depende solo de una variable. Por ejemplo, el conjunto de datos de puntos en una línea se puede considerar como un dato univariante donde la abscisa se puede considerar como una característica de entrada y la ordenada se puede considerar como una salida/resultado.
Por ejemplo:
Para la línea Y = 2X + 3 ;
La característica de entrada será X e Y será el resultado.
| X | Y |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
Concepto:
para la regresión lineal univariante, solo hay un vector de características de entrada. La línea de regresión tendrá la forma de:
Y = b0 + b1 * X
Donde,
b0 y b1 son los coeficientes de regresión.
Por tanto, se intenta predecir los coeficientes de regresión b0 y b1 entrenando un modelo.
Funciones de utilidad
- Predecir
defpredict(x, b0, b1):"""Predicts the value of prediction based oncurrent value of regression coefficients when input is x"""# Y = b0 + b1 * Xreturnb0+b1*x - Función de costo: la función
de costo calcula el porcentaje de error con el valor actual de los coeficientes de regresión. Define cuantitativamente hasta qué punto el modelo se compara con los coeficientes de regresión reales que tienen la tasa de error más baja.defcost(x, y, b0, b1):# y is a list of expected valueerrors=[]forx, yinzip(x, y):prediction=predict(x, b0, b1)expected=ydifference=prediction-expectederrors.append(difference)# Now, we have errors for all the observations,# for some input, the value of error might be positive# and for some input might be negative,# and if we directly add them up,# the values might cancel out leading to wrong output."# Hence, we use concept of mean squared error.# in mse, we return mean of square of all the errors.mse=sum([e*eforeinerrors])/len(errors)returnmse - Derivado de costos
Después de cada iteración, el costo se actualiza en proporción al error. La naturaleza del error es muy sensible a los datos. Por sensible a los datos me refiero a que el valor del error cambia muy rápido porque teníamos una función de error cuadrada. Por lo tanto, para hacerlo más tolerante a valores altos de errores, derivamos la función de error.
Las matemáticas son las siguientes:![Rendered by QuickLaTeX.com \begin{document} \begin{align*} cost(x, y) &= \frac{1}{m} \left( \sum_{i=1}^{n}\, (prediction(x_i)-y_i)^2 \right) \\ &= \frac{1}{m} \left( \sum_{i=1}^{n}\, (b0+b1*x_i-y_i)^2 \right) \end{align} \vspace{15} \begin{align*} cost\_derivative(x, y) &= \frac{\partial}{\partial b}\left( \frac{1}{m} \left( \sum_{i=1}^{n}\, (b0+b1*x_i-y_i)^2 \right) \right) \\ &= \frac{1}{m} \left( \sum_{i=1}^{n}\, \left(\frac{\partial}{\partial b}(b0+b1*x_i-y_i)^2\right) \right) \hspace{4ex} ....using DUIS \\ &= \frac{1}{m} \left( \sum_{i=1}^{n}\, \left(2*(b0+b1*x_i-y_i)*x_i^b \right) \right) \\ &= \frac{1}{m} \left( \sum_{i=1}^{n}\, \left(2*(prediction(x_i)-y_i)*x_i^b \right) \right) \\ \end{align} Where, \newline m = len(x) - is the number of rows in the dataset. \newline $x_i^b$- is x who's coefficient is b. \newline y = b_0+b_1 x_1 \newline $In this, b_1$is coefficient of $x_1$but coefficient of $b_0$is 1 \[ x_i^b = \begin{cases} 1 & i=0 \\ x_i & otherwise \end{cases} \] For this, we append an extra row consisting of 1's for $b_0$. \newline Or, add a switch case to the $cost\_derivative$function. \newline In our case, we will proceed with switch case. \newline \end{document}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c52bb85e3ec566e9cb1df09f6f5c5457_l3.png)
Código:
defcost_derivative(x, y, b0, b1, i):returnsum([2*(predict(xi, b0, b1)-yi)*1ifi==0else2*(predict(xi, b0, b1)-yi)*xiforxi, yiinzip(x, y)])/len(x) - Coeficientes de actualización:
en cada iteración (época), los valores del coeficiente de regresión se actualizan en un valor específico frente al error de la iteración anterior. Esta actualización es muy importante y es el quid de las aplicaciones de aprendizaje automático que escribe.
La actualización de los coeficientes con una actualización exacta de un coeficiente se realiza penalizando su valor con una fracción de error que causaron sus valores anteriores.
Esta fracción se denomina tasa de aprendizaje. Esto define qué tan rápido nuestro modelo llega al punto de convergencia (punto donde el error es idealmente 0).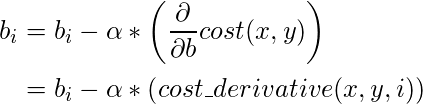
La función de Python para la misma es la siguiente:
defupdate_coeff(x, y, b0, b1, i, alpha):bi-=alpha*cost_derivative(x, y, b0, b1, i)returnbi - Detener iteraciones:
esta es la función que se utiliza para especificar cuándo deben detenerse las iteraciones.
Según el usuario, el algoritmo stop_iteration generalmente devuelve verdadero en las siguientes condiciones:- Iteración máxima: el modelo se entrena para un número específico de iteraciones.
- Valor del error: dependiendo del valor del error anterior, el algoritmo decide si continuar o detenerse.
- Precisión: dependiendo de la última precisión del modelo, si es mayor que la precisión mencionada, el algoritmo devuelve True,
- Híbrido: Esto se usa con más frecuencia. Esto combina más de una de las condiciones mencionadas anteriormente junto con una opción de descanso excepcional. El descanso excepcional es una condición en la que el entrenamiento continúa hasta que sucede algo malo. Algo malo podría incluir el desbordamiento de resultados, las limitaciones de tiempo excedidas, etc.
Teniendo todas las funciones de utilidad definidas, veamos el pseudocódigo seguido de su implementación:
Código:
x, y is the given data. (b0, b1) <-- (0, 0) i = 0 while True: if stop_iteration(i): break else: b0 = update_coeff(x, y, b0, b1, 0, alpha) b1 = update_coeff(x, y, b0, b1, 1, alpha)
Implementación final de Oop:
class LinearRegressor:
def __init__(self, x, y, alpha = 0.01, b0 = 0, b1 = 0):
"""
x: input feature
y: result / target
alpha: learning rate, default is 0.01
b0, b1: linear regression coefficient.
"""
self.i = 0
self.x = x
self.y = y
self.alpha = alpha
self.b0 = b0
self.b1 = b1
if len(x) != len(y):
raise TypeError("x and y should have same number of rows.")
def predict(model, x):
"""Predicts the value of prediction based on
current value of regression coefficients when input is x"""
# Y = b0 + b1 * X
return model.b0 + model.b1 * x
def cost_derivative(model, i):
x, y, b0, b1 = model.x, model.y, model.b0, model.b1
predict = model.predict
return sum([
2 * (predict(xi) - yi) * 1
if i == 0
else (predict(xi) - yi) * xi
for xi, yi in zip(x, y)
]) / len(x)
def update_coeff(model, i):
cost_derivative = model.cost_derivative
if i == 0:
model.b0 -= model.alpha * cost_derivative(i)
elif i == 1:
model.b1 -= model.alpha * cost_derivative(i)
def stop_iteration(model, max_epochs = 1000):
model.i += 1
if model.i == max_epochs:
return True
else:
return False
def fit(model):
update_coeff = model.update_coeff
model.i = 0
while True:
if model.stop_iteration():
break
else:
update_coeff(0)
update_coeff(1)
if __name__ == '__main__':
linearRegressor = LinearRegressor(
x =[i for i in range(12)],
y =[2 * i + 3 for i in range(12)],
alpha = 0.03
)
linearRegressor.fit()
print(linearRegressor.predict(12))
# expects 2 * 12 + 3 = 27
Publicación traducida automáticamente
Artículo escrito por RishabhBhatnagar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA