Relación entre gramática y lenguaje en Teoría de la Computación – Part 1

Una gramática es un conjunto de reglas de producción que se utilizan para generar strings de un lenguaje. En este artículo, hemos discutido cómo encontrar el lenguaje generado por una gramática y viceversa.

Lenguaje generado por una gramática –

Dada una gramática G, su lenguaje correspondiente L(G) representa el conjunto de todas las strings generadas a partir de G. Considere la siguiente gramática,

G: S-> aSb|ε

En esta gramática, usando S-> ε, podemos generar ε. Por lo tanto, ε es parte de L(G). De manera similar, usando S=>aSb=>ab, se genera ab. Del mismo modo, también se puede generar aabb.
Por lo tanto,

L(G) = {anbn, n>=0}

En el lenguaje L(G) discutido anteriormente, se toma la condición n = 0 para aceptar ε.
Puntos clave –

• Para una gramática G dada, su lengua correspondiente L(G) es única.
• El lenguaje L(G) correspondiente a la gramática G debe contener todas las strings que pueden generarse a partir de G.
• El lenguaje L(G) correspondiente a la gramática G no debe contener ninguna string que no pueda generarse a partir de G.

Discutamos preguntas basadas en esto:

Que-1. Considere la gramática: (GATE-CS-2009)

S -> aSa|bSb|a|b 

El lenguaje generado por la gramática anterior sobre el alfabeto {a,b} es el conjunto de:
(A) Todos los palíndromos
(B) Todos los palíndromos de longitud impar.
(C) Strings que comienzan y terminan con el mismo símbolo
(D) Todos los palíndromos de longitud uniforme

Solución: Usando S->a y S->b, se pueden generar a y b. De manera similar, usando S=>aSa=>aba, se puede generar aba. Otras strings que se pueden generar a partir de la gramática son: a, b, aba, bab, aaa, bbb, ababa,…
Por lo tanto, la opción (B) es correcta.

Que-2. Considere las siguientes gramáticas libres de contexto: (GATE-CS-2016)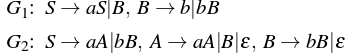

¿Cuál de los siguientes pares de lenguajes es generado por G1 y G2, respectivamente?

Solución: Considere la gramática G1:
Usando S=>B=>b, se puede generar b.
Utilizando S=>B=>bB, se puede generar bb.
Usando S=>aS=>aB=>ab se puede generar.
Usando S=>aS=>aB=>abB=>abb se puede generar.
Como podemos ver, el número de a puede ser cero o más, pero el número de b siempre es mayor que cero.
Por lo tanto,

L(G1) = {ambn| m>=0 and n>0}

Considere la gramática G2:
Usando S=>aA=>a, se puede generar a.
Usando S=>bB=>b, se puede generar b.
Usando S=>aA=>aaA=>aa se puede generar.
Usando S=>bB=>bbB=>bb se puede generar.
Utilizando S=>aA=>aB=>abB=>abb se puede generar.

Como podemos ver, a o b deben ser mayores que 0.
Por lo tanto,

L(G2) = {ambn| m>0 or n>0}

Gramática que genera un lenguaje dado –

Dada una lengua L(G), su correspondiente gramática G representa las reglas de producción que producen L(G). Considere el lenguaje L(G):

L(G) = {anbn, n>=0}

El lenguaje L(G) es un conjunto de strings ε, ab, aabb, aaabbb….
Para una string ε en L(G), la regla de producción puede ser S->ε.
Para otras strings en L(G), la regla de producción puede ser S->aSb|ε.
Por tanto, la gramática G correspondiente a L(G) es:

S->aSb| ε 

Puntos clave –

• Para un lenguaje L(G) dado, puede haber más de una gramática que pueda producir L(G).
• La gramática G correspondiente al lenguaje L(G) debe generar todas las strings posibles de L(G).
• La gramática G correspondiente al lenguaje L(G) no debe generar ninguna string que no sea parte de L(G).

Discutamos preguntas basadas en esto:

Que-3. ¿Cuál de las siguientes gramáticas genera el lenguaje L = {a ⁱ b ^j | i≠j}? (GATE-CS-2006)

Solución: El idioma dado L contiene las strings:

{a, b, aa, bb, aaa, bbb, aab, abb…}

Significa que la string debe contener uno o más números de a O uno o más números de b O a seguido de b que tiene un número diferente de a y b.

Si consideramos la gramática en la opción (A), puede generar ab como:

S=>AC=>aAC=>aC=>ab

Sin embargo, el lenguaje L no puede generar ab. Por lo tanto, la gramática en la opción (A) no es correcta.

De manera similar, la gramática en la opción (B) puede generar ab como:

S=>aS=>ab

Sin embargo, el idioma L no puede generar ab. Por lo tanto, la gramática en la opción (B) no es correcta.

De manera similar, la gramática en la opción (C) puede generar ab como:

S=>AC=>C=>aCb=>ab

Sin embargo, el lenguaje L no puede generar ab. Por lo tanto, la gramática en la opción (C) no es correcta.
Por lo tanto, usando el método de eliminación, la opción (D) es correcta.