Una función booleana se describe mediante una expresión algebraica que consiste en variables binarias, las constantes 0 y 1 y los símbolos de operación lógica. ![]()
Para un conjunto dado de valores de las variables binarias involucradas, la función booleana puede tener un valor de 0 o 1. Para ejemplo, la función booleana ![]() se define en términos de tres variables binarias
se define en términos de tres variables binarias ![]() . La función es igual a 1 si
. La función es igual a 1 si ![]() y
y ![]() simultáneamente o
simultáneamente o ![]() .
.
Cada función booleana se puede expresar mediante una expresión algebraica, como la mencionada anteriormente, o en términos de una tabla de verdad. Una función puede expresarse mediante varias expresiones algebraicas, por ser lógicamente equivalentes, pero sólo existe una única tabla de verdad para cada función.
Una función booleana se puede transformar de una expresión algebraica a un diagrama de circuito compuesto por puertas lógicas conectadas en una estructura particular. Diagrama de circuito para ![]() –
–

Formas canónicas y estándar:
cualquier variable binaria puede tomar una de dos formas, ![]() o
o ![]() . Una función booleana se puede expresar en términos de
. Una función booleana se puede expresar en términos de ![]() variables binarias. Si todas las variables binarias se combinan juntas usando la operación AND, entonces hay un total de
variables binarias. Si todas las variables binarias se combinan juntas usando la operación AND, entonces hay un total de ![]() combinaciones ya que cada variable puede tomar dos formas.
combinaciones ya que cada variable puede tomar dos formas.
Cada una de las combinaciones se denomina minitérmino o producto estándar . Un minitérmino está representado por ![]() donde
donde ![]() es el equivalente decimal del número binario al que se designa el minitérmino.
es el equivalente decimal del número binario al que se designa el minitérmino.
Nota importante: en un término mínimo, la variable binaria no está primada si la variable es 1 y está primada si la variable es 0, es decir, si el término mínimo es ![]() entonces eso significa
entonces eso significa![]() y
y ![]() .
.
Por ejemplo, para una función booleana en dos variables, los minitérminos son:![]()
De manera similar, si las variables se combinan con la operación OR, el término obtenido se denomina maxterm o suma estándar . Un maxterm está representado por ![]() donde
donde ![]() es el equivalente decimal del número binario al que se designa el maxterm.
es el equivalente decimal del número binario al que se designa el maxterm.
Nota importante: en un término máximo, la variable binaria no está primada si la variable es 0 y está primada si la variable es 1, es decir, si el término máximo es ![]() entonces eso significa
entonces eso significa ![]() y
y ![]() .
.
Por ejemplo, para una función booleana en dos variables, los términos máximos son:![]()
Minitérminos y Maxtérminos para función en 3 variables –

Relación entre Mintérminos y Maxtérminos – Cada minitérmino es el complemento de su correspondiente maxtérmino.
Por ejemplo, para una función booleana en dos variables:
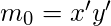

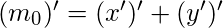
In general
or
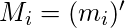
Construcción de funciones booleanas: ahora que sabemos qué son los términos mínimos y máximos, podemos usarlos para construir expresiones booleanas.
«Una función booleana se puede expresar algebraicamente a partir de una tabla de verdad dada formando un término mínimo para cada combinación de las variables que produce un 1 en la función y luego tomando el OR de todos esos términos».
Por ejemplo, considere dos funciones ![]() y
y ![]() con las siguientes tablas de verdad:
con las siguientes tablas de verdad:
| X | y | z | F 1 | F 2 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
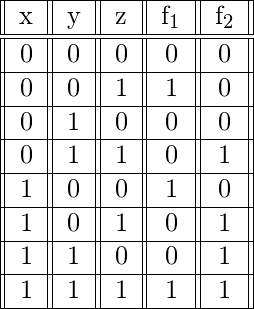
La función
![]()
es 1 para las siguientes combinaciones de
![]()
– 001,100,111
Los minitérminos correspondientes son-
![]()
,
![]()
,
![]()
.
Por lo tanto, la expresión algebraica para
![]()
es-
![]()
![]()
De manera similar, la expresión algebraica para
![]()
es-
![]()
Si usamos la ley de De Morgans en
![]()
y
![]()
todos los 1 se convierten en 0 y todos los 0 se convierten en 1. Por lo tanto, obtenemos-
![]()
![]()
Sobre el uso de la Ley de De Morgan de nuevo-
![]()
![]()
![]()
y
![]()
![]()
![]()
Podemos concluir de lo anterior que las funciones booleanas se pueden expresar como
suma de minitérminos
o un
producto de maxterms
.
“Se dice que las funciones booleanas expresadas como suma de minitérminos o producto de maxtérminos están en forma canónica .
- Ejemplo 1: exprese la siguiente expresión booleana en formularios SOP y POS:
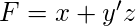
- Solución: la expresión se puede transformar en formato SOP agregando variables faltantes en cada término multiplicando por
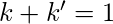 dónde
dónde 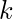 está la variable faltante.
está la variable faltante.
Se deduce del hecho de que:
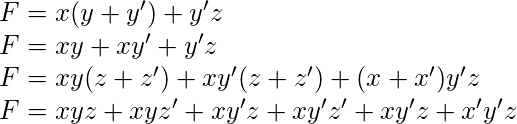
Al reorganizar los términos mínimos en orden ascendente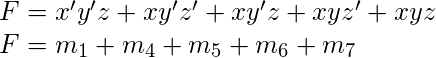
Si queremos el formulario POS, podemos negar dos veces el formulario SOP como se indicó anteriormente para obtener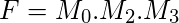
: Los formularios SOP y POS tienen una notación breve de representación :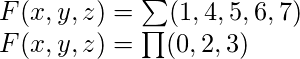
Formas estándar:
las formas canónicas son formas básicas que se obtienen de la tabla de verdad de la función. Estas formas generalmente no se utilizan para representar la función, ya que son engorrosas de escribir y es preferible representar la función en el menor número de literales posible.
Hay dos tipos de formularios estándar:
- Suma de productos (SOP): una expresión booleana que involucra términos AND con uno o más literales cada uno, combinados con OR.
- Producto de sumas (POS) Una expresión booleana que implica términos OR con uno o más literales cada uno, combinados con AND, p. ej.
SOP-
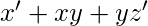 POS-
POS- 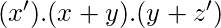
Nota: las expresiones anteriores no son equivalentes, son solo ejemplos.
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
1. GATE CS 2010, Pregunta 6
2. GATE CS 2008, Pregunta 7
3. GATE CS 2014 Conjunto-1, Pregunta 17
Referencias-
Diseño digital 5ª edición, por Morris Mano y Michael Ciletti
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA