Representación de Números Binarios Negativos

Dado que los números binarios solo pueden tener dos símbolos, ya sea 0 o 1 para cada posición o bit, no es posible agregar símbolos menos o más delante de un número binario.

Representamos números binarios negativos usando un símbolo menos delante de ellos. En la representación de números por computadora, estos números se pueden distinguir con la ayuda de un bit adicional o indicador llamado bit de signo o indicador de signo en el sistema de representación de números binarios para números con signo. Este bit adicional se denomina bit de signo o bandera de signo y tiene un valor de bit de signo de 0 para números positivos y 1 para números binarios negativos.

La representación de la magnitud de los números positivos es fácil y no necesita ningún cambio.

La representación de la magnitud de los números negativos se cambia en consecuencia para representarla.

Formas de representar magnitudes:
Estas son: Método Signo-Magnitud, Método Complemento a 1 y Método Complemento a 2. Estos se explican a continuación mediante ejemplos.

1. Método de magnitud con signo:
   solo agregamos un bit de signo adicional para reconocer números negativos y positivos. El bit de signo tiene 1 para número negativo y 0 para número positivo.

   

   Rango de números:
   para un registro de n bits, MSB será un bit de signo y (n-1) bits será una magnitud. Entonces,
   el número negativo más bajo que se puede almacenar es -(2 ^(k-1) -1) y el número positivo más grande que se puede almacenar es (2 ^(k-1) -1).

   Pero, esta representación (signo) tiene una representación ambigua del número 0. Significa que 0 tiene dos representaciones diferentes, una es -0 (p. ej., 1 00000 en un registro de seis bits) y la segunda es +0 (p. ej., 0 00000 en un registro de seis bits). ).

   

2. Método de complemento de 1
   : tenga en cuenta que MSB siempre es un bit de signo, si es 0, entonces no hay cambios. MSB siempre es 1 en caso de números negativos. Solo tomamos el complemento de 1 de números negativos para representar en la computadora.

   

   Rango de números:
   para el registro de n bits, el número negativo más bajo que se puede almacenar es -(2 ^(n-1) -1) y el número positivo más grande que se puede almacenar es (2 ^(n-1) -1).

   Pero, esta representación (de signo) tiene una representación ambigua del número 0. Significa que 0 tiene dos representaciones diferentes, una es -0 (p. ej., 1 1111 en un registro de cinco bits) y la segunda es +0 (p. ej., 0 0000 en un registro de cinco bits). ).

   

3. Método de complemento a 2
   : tenga en cuenta que MSB siempre es un bit de signo, si es 0, entonces no hay cambios. MSB siempre es 1 en caso de números negativos. Solo tomamos complemento de 2 de números negativos para representar en la computadora.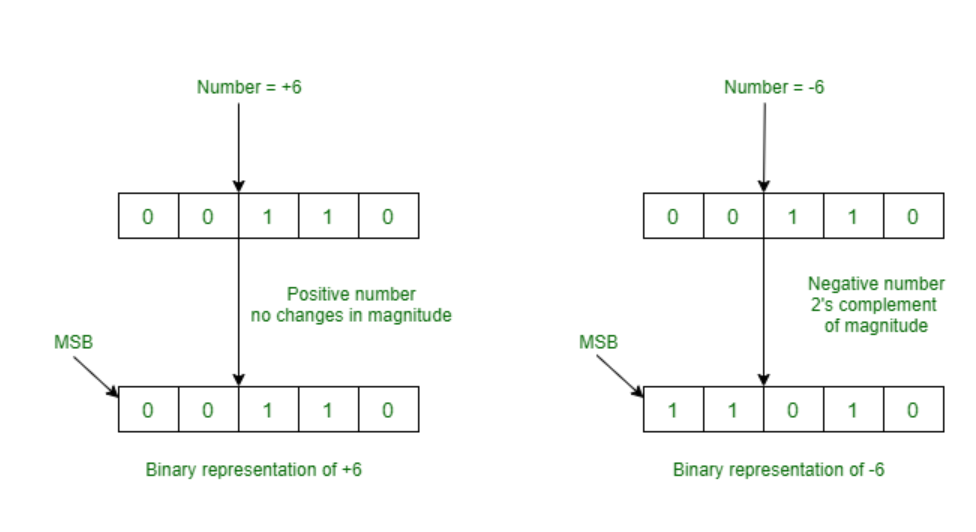

   

   Dado que solo hay una representación de +0 y -0, esta representación en complemento a 2 es mejor que la representación de signo y la representación en complemento a 1.

   

   Rango de números:
   para el registro de n bits, el número negativo más bajo que se puede almacenar es -(2 ^(n-1) ) y el número positivo más grande que se puede almacenar es (2 ^(n-1) -1).