Si la mayoría de los elementos de la array son cero, la array se denomina array dispersa. Es un desperdicio almacenar los elementos cero en la array ya que no afectan los resultados de nuestro cálculo. Es por eso que implementamos estas arrays en representaciones más eficientes que la array 2D estándar. Usando representaciones más eficientes, podemos reducir significativamente las complejidades de espacio y tiempo de las operaciones.
Hemos discutido en 4 representaciones diferentes en los siguientes artículos:
En este artículo, discutiremos otra representación de la array dispersa que se conoce comúnmente como el formato de Yale.
El CSR (fila dispersa comprimida) o el formato de Yale es similar a la representación de array (discutida en el conjunto 1) de array dispersa. Representamos una array M (m * n), mediante tres arrays o vectores 1-D llamados A, IA, JA. Deje que NNZ denote el número de elementos distintos de cero en M y tenga en cuenta que se utiliza la indexación basada en 0.
- El vector A es de tamaño NNZ y almacena los valores de los elementos distintos de cero de la array. Los valores aparecen en el orden de atravesar la array fila por fila
- El vector IA es de tamaño m+1 almacena el número acumulativo de elementos distintos de cero hasta (sin incluir) la i-ésima fila. Se define por la relación recursiva:
- IA[0] = 0
- IA[i] = IA[i-1] + número de elementos distintos de cero en la (i-1) ésima fila de la Array
- El vector JA almacena el índice de columna de cada elemento en el vector A. Por lo tanto, también es de tamaño NNZ.
Para encontrar el número de elementos distintos de cero en la fila i, realizamos IA[i+1] – IA[i]. Observe cómo esta representación es diferente a la implementación basada en array donde el segundo vector almacena los índices de fila de elementos distintos de cero.
Los siguientes ejemplos muestran cómo se representan estas arrays.
Ejemplos:
Input : 0 0 0 0
5 8 0 0
0 0 3 0
0 6 0 0
Solution: When the matrix is read row by
row, the A vector is [ 5 8 3 6]
The JA vector stores column indices
of elements in A hence, JA = [ 0 1 2
1]. IA[0] = 0. IA[1] = IA[0] + no
of non-zero elements in row 0
i.e 0 + 0 = 0.
Similarly,
IA[2] = IA[1] + 2 = 2
IA[3] = IA[2] + 1 = 3
IA[4] = IA[3]+1 = 4
Therefore IA = [0 0 2 3 4]
The trick is remember that IA[i]
stores NNZ upto and not-including
i row.
Input : 10 20 0 0 0 0
0 30 0 4 0 0
0 0 50 60 70 0
0 0 0 0 0 80
Output : A = [10 20 30 4 50 60 70 80],
IA = [0 2 4 7 8]
JA = [0 1 1 3 2 3 4 5]
Algoritmo:
SPARSIFY (MATRIX)
Step 1: Set M to number of rows in MATRIX
Step 2: Set N to number of columns in MATRIX
Step 3: I = 0, NNZ = 0. Declare A, JA, and IA.
Set IA[0] to 0
Step 4: for I = 0 ... N-1
Step 5: for J = 0 ... N-1
Step 5: If MATRIX [I][J] is not zero
Add MATRIX[I][J] to A
Add J to JA
NNZ = NNZ + 1
[End of IF]
Step 6: [ End of J loop ]
Add NNZ to IA
[ End of I loop ]
Step 7: Print vectors A, IA, JA
Step 8: END
Implementación:
CPP
// CPP program to find sparse matrix rep-
// resentation using CSR
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef std::vector<int> vi;
typedef vector<vector<int> > matrix;
// Utility Function to print a Matrix
void printMatrix(const matrix& M)
{
int m = M.size();
int n = M[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++)
cout << M[i][j] << " ";
cout << endl;
}
}
// Utility Function to print A, IA, JA vectors
// with some decoration.
void printVector(const vi& V, char* msg)
{
cout << msg << "[ ";
for_each(V.begin(), V.end(), [](int a) {
cout << a << " ";
});
cout << "]" << endl;
}
// Generate the three vectors A, IA, JA
void sparesify(const matrix& M)
{
int m = M.size();
int n = M[0].size(), i, j;
vi A;
vi IA = { 0 }; // IA matrix has N+1 rows
vi JA;
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i][j] != 0) {
A.push_back(M[i][j]);
JA.push_back(j);
// Count Number of Non Zero
// Elements in row i
NNZ++;
}
}
IA.push_back(NNZ);
}
printMatrix(M);
printVector(A, (char*)"A = ");
printVector(IA, (char*)"IA = ");
printVector(JA, (char*)"JA = ");
}
// Driver code
int main()
{
matrix M = {
{ 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 },
};
sparesify(M);
return 0;
}
Java
import java.util.*;
// Java program to find sparse matrix
// resentation using CSR
public class GFG {
// Utility Function to print a Matrix
private static void printMatrix(int[][] M)
{
int m = M.length;
int n = (M.length == 0 ? 0 : M[0].length);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(M[i][j] + " ");
}
System.out.println();
}
}
// Utility Function to print A, IA, JA vectors
// with some decoration.
private static void printVector(ArrayList<Integer> V,
String msg)
{
System.out.print(msg + "[ ");
for (var a : V) {
System.out.print(a + " ");
}
System.out.println("]");
}
// Generate the three vectors A, IA, JA
private static void sparesify(int[][] M)
{
int m = M.length;
int n = (M.length == 0 ? 0 : M[0].length), i, j;
ArrayList<Integer> A = new ArrayList<Integer>();
ArrayList<Integer> IA
= new ArrayList<Integer>(); // IA matrix has N+1
// rows
ArrayList<Integer> JA = new ArrayList<Integer>();
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i][j] != 0) {
A.add(M[i][j]);
JA.add(j);
// Count Number of Non Zero
// Elements in row i
NNZ++;
}
}
IA.add(NNZ);
}
printMatrix(M);
printVector(A, "A = ");
printVector(IA, "IA = ");
printVector(JA, "JA = ");
}
// Driver code
public static void main(String[] args)
{
int[][] M = { { 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 } };
// Function call
sparesify(M);
}
}
// This code is contributed by Aarti_Rathi
C#
// C# program to find sparse matrix
// resentation using CSR
using System;
using System.Collections.Generic;
class GFG {
// Utility Function to print a Matrix
static void printMatrix(int[, ] M)
{
int m = M.GetLength(0);
int n = M.GetLength(1);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++)
Console.Write(M[i, j] + " ");
Console.WriteLine();
}
}
// Utility Function to print A, IA, JA vectors
// with some decoration.
static void printVector(List<int> V, string msg)
{
Console.Write(msg + "[ ");
foreach(var a in V) { Console.Write(a + " "); }
Console.WriteLine("]");
}
// Generate the three vectors A, IA, JA
static void sparesify(int[, ] M)
{
int m = M.GetLength(0);
int n = M.GetLength(1), i, j;
List<int> A = new List<int>();
List<int> IA
= new List<int>(); // IA matrix has N+1 rows
List<int> JA = new List<int>();
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i, j] != 0) {
A.Add(M[i, j]);
JA.Add(j);
// Count Number of Non Zero
// Elements in row i
NNZ++;
}
}
IA.Add(NNZ);
}
printMatrix(M);
printVector(A, "A = ");
printVector(IA, "IA = ");
printVector(JA, "JA = ");
}
// Driver code
public static void Main()
{
int[, ] M = {
{ 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 },
};
// Function call
sparesify(M);
}
}
// This code is contributed by Aarti_Rathi
0 0 0 0 1 5 8 0 0 0 0 0 3 0 0 0 6 0 0 1 A = [ 1 5 8 3 6 1 ] IA = [ 0 1 3 4 6 ] JA = [ 4 0 1 2 1 4 ]
Complejidad temporal: O(nxm)
Espacio auxiliar: O(n + m)
notas
- La dispersión de la array = (Número total de elementos – Número de elementos distintos de cero) / (Número total de elementos) o (1 – NNZ/mn) o (1 – tamaño(A)/mn).
- La representación basada en array directa requería memoria 3 * NNZ mientras que CSR requiere (2 * NNZ + m + 1) memoria.
- Las arrays CSR son eficientes en memoria siempre que
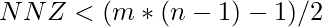 .
. - Similar a CSR, sale CSC, que significa Columnas dispersas comprimidas. Es el análogo de columna para CSR.
- El formato ‘Nuevo’ de Yale comprime aún más los vectores A y JA en 1 vector.
Este artículo es una contribución de Aarti_Rathi . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por Sayan Mahapatra y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA