Resolución de ecuaciones en diferencias homogéneas de segundo orden en MATLAB

Las ecuaciones en diferencias son ecuaciones matemáticas que involucran las diferencias entre valores generalmente sucesivos de una función (‘y’) de una variable discreta. Aquí, una variable discreta significa que se define solo para valores que difieren en una cantidad finita, generalmente una constante (generalmente ‘1’). Una ecuación en diferencias también se puede definir como una relación entre la diferencia de una función desconocida en uno o más valores generales como es el argumento. Por ejemplo, la ecuaciónΔy _n+1 +y _n = 2, también se puede reescribir como: y _n+2 -y _n+1 +y _n = 2 (Ya que, Δy _n = y _n+1 -y _n )

Orden de una Ecuación en Diferencia:

El Orden de una Ecuación en Diferencia se puede encontrar por la Relación: 

Ejemplo: considere la ecuación 3y _n+2 -y _n+1 +5y _n = -12, el orden es:

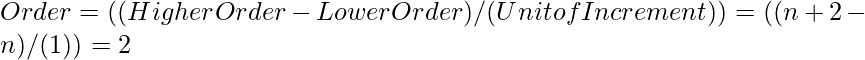
Por lo tanto, el orden de la ecuación anterior es ‘2’. Por lo tanto, puede llamarse una ecuación de diferencia de segundo ^orden específica.

Homogéneo: si el RHS de la ecuación anterior es cero, entonces se puede llamar una ecuación de diferencia homogénea de segundo ^orden en específico. 

Pasos para resolver una ^ecuación en diferencia homogénea de segundo orden  :

Paso 1: Deje que la ecuación de diferencia de segundo orden dada sea:

ayn+2+byn+1+cyn = 0

Paso 2: Luego, reducimos la ecuación de diferencia de segundo orden anterior a su forma de ecuación auxiliar (AE):

ar2+br+c = 0

Paso 3: Luego, encontramos el Determinante de la Ecuación Auxiliar (AE) anterior por la Relación:

Det = (b2 − 4ac)

Paso 4: Si el Determinante encontrado arriba es Positivo (2 Raíces Reales Distintas r ₁ & r ₂ ), entonces el y _n será:

yn = C1r1n + C2r2n

Paso 5: De lo contrario, si el Determinante encontrado arriba es Cero (2 Raíz Real Igual,r ₁ =r ₂ =r), entonces el y _n será:

yn = (C1n + C2)r1n

Paso 6: De lo contrario, si el Determinante encontrado arriba es Negativo (Raíces Complejas, r = α ± iβ), entonces el y _n será: 

yn = Pn(C1cos(nθ) + C2sin(nθ)),
where P = √(α2+β2) and θ = tan-1(β/α)

Si se dan algunas condiciones iniciales, como y ₀ = m y y ₁ = n, entonces sustituimos estas dos ecuaciones en la ecuación anterior y luego encontramos C1 y C2 resolviendo la ecuación que formamos anteriormente por sustitución. Luego reemplazamos el C ₁ y C ₂ encontrado en la ecuación ‘y _n ‘.

Las funciones de MATLAB utilizadas en el siguiente código son:

• disp(‘txt’): este método muestra el mensaje ‘txt’ al usuario.
• input(‘txt’): este método muestra el ‘txt’ y espera a que el usuario ingrese un valor y presione la tecla Retorno.
• solve(eq): este método resuelve el ‘eq’ para la variable presente en él.
• abs(z): este método devuelve el módulo complejo de z.
• angle(z): este método devuelve el ángulo de fase en el intervalo [-π,π] de z.
• subs(y, old, new): este método devuelve una copia de y, reemplazando todas las apariciones de old con new.
• simplificar (eq): este método realiza la simplificación algebraica de ‘eq’.

Ejemplo 1:

% MATLAB CODE (WITHOUT INITIAL CONDITIONS):
% To clear all variables from the current workspace
clear all  
  
% To clear all the text from the Command Window, resulting in a clear screen
clc        
disp("Solving 2nd Order Homogeneous Difference Equations in MATLAB | GeeksforGeeks")
  
% To Declare them as Variables
syms r c1 c2 n  
F=input('Input the coefficients [a,b,c]: ');
  
% Coefficients of the 2nd Order Difference Equation
a=F(1);b=F(2);c=F(3);  
  
% Auxiliary Equation Formed
eq=a*(r^2)+b*(r)+c;    
S=solve(eq);
  
% Roots of the Auxiliary Equation Formed
r1=S(1);r2=S(2);       
  
% Determinant of the Auxiliary Equation Formed
D=b^2-4*a*c;           
if D>0
    y1=(r1)^n;
    y2=(r2)^n;
    yn=c1*y1+c2*y2;
elseif D==0
    y1=(r1)^n;
    y2=n*((r2)^n);
    yn=c1*y1+c2*y2;
else
    P=abs(r1);
    t=angle(r1);
    y1=((P)^n)*cos(n*t);
    y2=((P)^n)*sin(n*t);
    yn=c1*y1+c2*y2;
end
disp ('The solution of the difference equation yn=')
disp(yn)

Producción:

 

 

Ejemplo 2:

% MATLAB CODE (WITH INITIAL CONDITIONS):
% To clear all variables from the current workspace
clear all  
clc        
disp("Solving 2nd Order Homogeneous Difference Equations in MATLAB | GeeksforGeeks")
  
% To Declare them as Variables
syms r c1 c2 n  
F=input('Input the coefficients [a,b,c]: ');
  
% Coefficients of the 2nd Order Difference Equation
a=F(1);b=F(2);c=F(3);  
  
% Auxiliary Equation Formed
eq=a*(r^2)+b*(r)+c;    
S=solve(eq);
  
% Roots of the Auxiliary Equation Formed
r1=S(1);r2=S(2);       
  
% Determinant of the Auxiliary Equation Formed
D=b^2-4*a*c;          
if D>0
    y1=(r1)^n;
    y2=(r2)^n;
    yn=c1*y1+c2*y2;
elseif D==0
    y1=(r1)^n;
    y2=n*((r2)^n);
    yn=c1*y1+c2*y2;
else
    P=abs(r1);
    t=angle(r1);
    y1=((P)^n)*cos(n*t);
    y2=((P)^n)*sin(n*t);
    yn=c1*y1+c2*y2;
end
IC=input('Enter the initial conditions in the form [y0,y1]:');
  
% Initial conditions
y0=IC(1);y1=IC(2);      
eq1=subs(yn,n,0)-y0;
eq2=subs(yn,n,1)-y1;
  
% Finding C1 & C2
[c1,c2]=solve(eq1,eq2); 
yn=simplify(subs(yn));
disp ('The solution of the difference equation yn=')
disp(yn)

Producción: