Resolución de problemas en array de dispersión

Requisito previo: Array de gráfico de dispersión

Calculamos S _w (dentro de la array de dispersión de clase) y S _B (entre la array de dispersión de clase) para los puntos de datos disponibles.

S _W : Para minimizar la variabilidad dentro de una clase, dispersión de clase interna.
S _B : Para aumentar la variabilidad entre clases, la dispersión entre clases.

diagrama de dispersión de los puntos

X1 = (y1, y2) ={ (2,2), (1,2), (1,2), (1,2), (2,2) }
X2 = (y1,y2) ={ (9, 10), (6,8), (9,5), (8,7), (10,8) }

Dentro de la array de dispersión de clase:

$S_W = \sum_{i=1}^{c}S_i \\ S_i = \sum_{x\in D_i}^{c} (x-m_i)(x-m_i)^{T}$

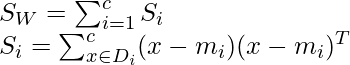
S_i is the class specific covariance matrix.
m_i is the mean of individual class

Cálculo medio:

Calculamos la media para cada uno de los puntos presentes en la clase. Aquí la media es la suma total de las observaciones dividida por el número de observaciones, requerimos esta media para calcular la covarianza de la array.

$m_1 = [\frac{2+1+1+1+2}{5} , \frac{2+2+2+2+2}{5} ] \\ = [1.4,2]$

$m_2 = [\frac{9+6+9+8+10}{5} , \frac{10+8+5+7+8}{5} ] \\ = [8.4,7.6]$

Cálculo de la array de covarianza:
restamos el valor medio de cada una de las observaciones y luego calculamos el promedio después de realizar la multiplicación de la array con la transpuesta de la array.

Covarianza específica de clase para la primera clase:

$(X1-m_1) = \begin{bmatrix} 0.6 & -0.4 & -0.4 & -0.4 & 0.6\\ 0 & 0 & 0& 0& 0 \end{bmatrix}$

$1) \begin{bmatrix} 0.6 \\ 0 \end{bmatrix} * \begin{bmatrix} 0.6 &0 \end{bmatrix} = \begin{bmatrix} 0.36 &0 \\ 0 &0 \end{bmatrix} \\\\ 2) \begin{bmatrix} -0.4 \\ 0 \end{bmatrix} * \begin{bmatrix} -0.4 &0 \end{bmatrix} = \begin{bmatrix} 0.16 &0 \\ 0 &0 \end{bmatrix} \\\\ 3) \begin{bmatrix} -0.4 \\ 0 \end{bmatrix} * \begin{bmatrix} -0.4 &0 \end{bmatrix} = \begin{bmatrix} 0.16 &0 \\ 0 &0 \end{bmatrix} \\\\ 4) \begin{bmatrix} -0.4 \\ 0 \end{bmatrix} * \begin{bmatrix} -0.4 &0 \end{bmatrix} = \begin{bmatrix} 0.16 &0 \\ 0 &0 \end{bmatrix} \\\\ 5) \begin{bmatrix} 0.6 \\ 0 \end{bmatrix} * \begin{bmatrix} 0.6 &0 \end{bmatrix} = \begin{bmatrix} 0.36 &0 \\ 0 &0 \end{bmatrix} \\\\$

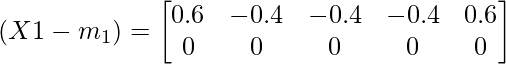
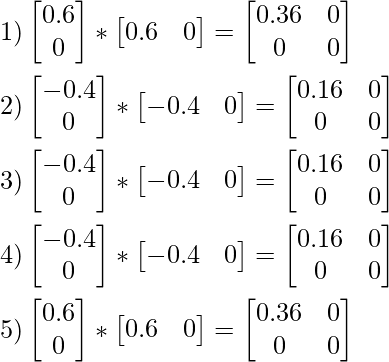
Promediando valores de 1,2,3,4 y 5.
Calculamos la suma de todos los valores para cada elemento en la array para S1 y dividimos por el número de la observación que en el presente cálculo es 5.

$matrix_{00} = \frac{ 0.36+0.16+0.16+0.16+0.36}{5}\\ =\frac{1.2}{5}\\ = 0.24\\\\ matrix_{01} = \frac{ 0+0+0+0+0}{5}\\ = 0\\\\ matrix_{10} = \frac{ 0+0+0+0+0}{5}\\ = 0\\\\ matrix_{11} = \frac{ 0+0+0+0+0}{5}\\ = 0\\\\$

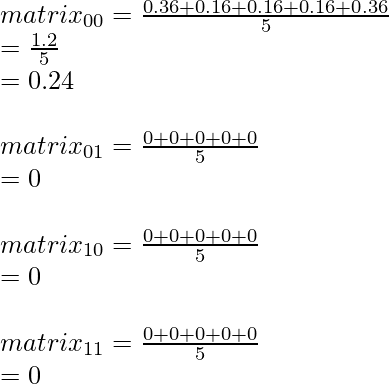
_{Por lo tanto} S1 es:

$S_1 = \begin{bmatrix} 0.24 &0 \\ 0 &0 \end{bmatrix}$

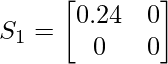
Covarianza específica de clase para la segunda clase:

$(X2-m_2) = \begin{bmatrix} 0.6 & -2.4 & 0.6 & -0.4 & 1.6\\ 2.4 & 0.4 & -2.6& -0.6& 0.4 \end{bmatrix}$

$1) \begin{bmatrix} 0.6 \\ 2.4 \end{bmatrix} * \begin{bmatrix} 0.6 &2.4 \end{bmatrix} = \begin{bmatrix} 0.36 &1.44 \\ 1.44 &05.76 \end{bmatrix} \\\\ 2) \begin{bmatrix} -2.4 \\ 0.4 \end{bmatrix} * \begin{bmatrix} -2.4 &0.4 \end{bmatrix} = \begin{bmatrix} 5.76 &-0.96 \\ -0.96 &0.16 \end{bmatrix} \\\\ 3) \begin{bmatrix} 0.6 \\ -2.6 \end{bmatrix} * \begin{bmatrix} 0.6 &-2.6 \end{bmatrix} = \begin{bmatrix} 0.36 &-1.56 \\ 1.56 &6.76 \end{bmatrix} \\\\ 4) \begin{bmatrix} -0.4 \\ -0.6 \end{bmatrix} * \begin{bmatrix} -0.4 &-0.6 \end{bmatrix} = \begin{bmatrix} 0.16 &0.24 \\ 0.24 &0.36 \end{bmatrix} \\\\ 5) \begin{bmatrix} 1.6 \\ 0.4 \end{bmatrix} * \begin{bmatrix} 1.6 &0.4 \end{bmatrix} = \begin{bmatrix} 2.56 &0.64 \\ 0.64 &0.16 \end{bmatrix} \\\\$

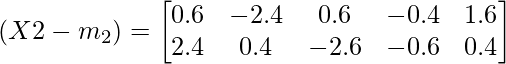
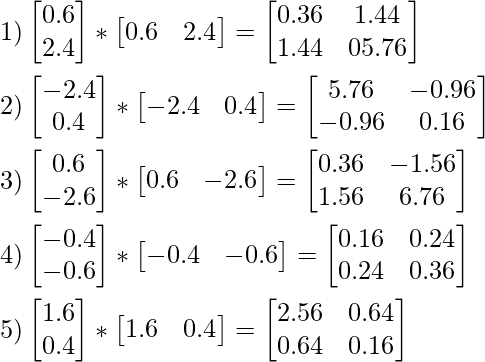
Promediando los valores de 1, 2, 3, 4 y 5
, calculamos la suma de todos los valores de cada elemento en la array para S2 y la dividimos por el número de la observación, que en el presente cálculo es 5.

$matrix_{00} = \frac{ 0.36+5.76+0.36+0.16+2.56}{5}\\ =\frac{9.2}{5}\\ = 1.84\\\\ matrix_{01} = \frac{ 1.44-0.96-1.56+0.24+0.64}{5}\\ =\frac{-0.2}{5}\\ = -0.04\\\\ matrix_{10} = \frac{ 1.44-0.96-1.56+0.24+0.64}{5}\\ =\frac{-0.2}{5}\\ = -0.04\\\\ matrix_{11} = \frac{ 5.76+0.16+6.76+0.36+0.16}{5}\\ =\frac{13.2}{5}\\ = 2.64\\\\$

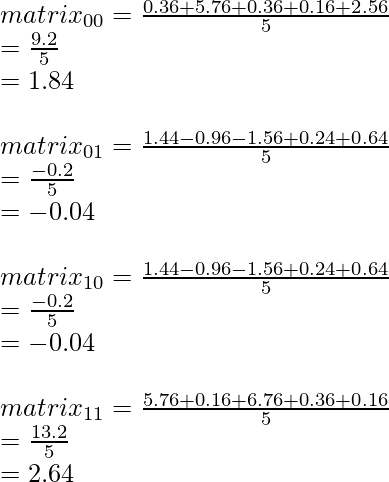
Por lo tanto S2 es:

$S_2 = \begin{bmatrix} 1.84 &-0.04 \\ -0.04 &2.64 \end{bmatrix}$

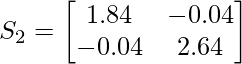
Dentro de la array de dispersión de clase S _w :

S_W= S₁ + S₂

$S_W= \begin{bmatrix} 0.24 &0 \\ 0 &0 \end{bmatrix} + \begin{bmatrix} 1.84 &-0.04 \\ -0.04 &2.64 \end{bmatrix} \\\\ =\begin{bmatrix} 2.08 &-0.04 \\ -0.04 &2.64 \end{bmatrix}$

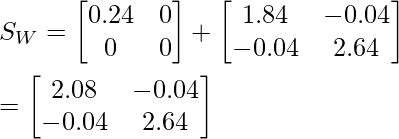
Entre la array de dispersión de clases S _B :

$S_B = (m_1 - m_2) * (m_1 - m_2)^{T}\\\\ S_B = \begin{bmatrix} 7 & 5.6 \end{bmatrix} * \begin{bmatrix} 7 \\5.6 \end{bmatrix} \\\\ =\begin{bmatrix} 49 &37.2 \\ 37.2 &31.36 \end{bmatrix}$

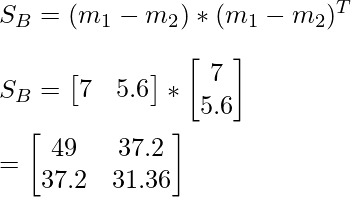
Array de dispersión total:

S_{T = SB + SW}

$S_w =\begin{bmatrix} 49 &37.2 \\ 37.2 &31.36 \end{bmatrix} + \begin{bmatrix} 2.08 &-0.04 \\ -0.04 &2.64 \end{bmatrix} \\ =\begin{bmatrix} 51.08 & 37.16 \\ 37.16 &34 \end{bmatrix}$

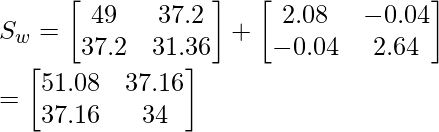
Por lo tanto, hemos calculado entre la array de dispersión de clase y la array de dispersión dentro de la clase para los puntos de datos disponibles.

Hacemos uso de estos cálculos en la extracción de características, donde el objetivo principal es aumentar la distancia entre la clase en la proyección de puntos y disminuir la distancia entre los puntos dentro de la clase en la proyección. Aquí nuestro objetivo es generar una proyección de datos en la dimensión requerida.

Publicación traducida automáticamente

Artículo escrito por deviprajwala y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta