Requisitos previos :
retrocediendoes una técnica algorítmica para resolver problemas recursivamente al tratar de construir una solución de forma incremental, una pieza a la vez, eliminando aquellas soluciones que no satisfacen las restricciones del problema en cualquier punto en el tiempo (por tiempo, aquí, se hace referencia al tiempo transcurrido hasta alcanzar cualquier nivel del árbol de búsqueda). El retroceso también se puede decir como una mejora del enfoque de fuerza bruta. Básicamente, la idea detrás de la técnica de retroceso es que busca una solución a un problema entre todas las opciones disponibles. Inicialmente, comenzamos el retroceso desde una opción posible y si el problema se resuelve con esa opción seleccionada, devolvemos la solución; de lo contrario, retrocedemos y seleccionamos otra opción de las opciones disponibles restantes. También puede haber un caso en el que ninguna de las opciones le brinde la solución y, por lo tanto, entendemos que retroceder no brindará ninguna solución a ese problema en particular. También podemos decir que el retroceso es una forma de recursividad. Esto se debe a que el proceso de encontrar la solución entre las distintas opciones disponibles se repite recursivamente hasta que no encontramos la solución o llegamos al estado final. Entonces, podemos concluir que retroceder en cada paso elimina aquellas opciones que no pueden darnos la solución y procede a aquellas opciones que tienen el potencial de llevarnos a la solución. Esto se debe a que el proceso de encontrar la solución entre las distintas opciones disponibles se repite recursivamente hasta que no encontramos la solución o llegamos al estado final. Entonces, podemos concluir que retroceder en cada paso elimina aquellas opciones que no pueden darnos la solución y procede a aquellas opciones que tienen el potencial de llevarnos a la solución. Esto se debe a que el proceso de encontrar la solución entre las distintas opciones disponibles se repite recursivamente hasta que no encontramos la solución o llegamos al estado final. Entonces, podemos concluir que retroceder en cada paso elimina aquellas opciones que no pueden darnos la solución y procede a aquellas opciones que tienen el potencial de llevarnos a la solución.
Según la definición de wiki,
El backtracking se puede definir como una técnica algorítmica general que considera buscar todas las combinaciones posibles para resolver un problema computacional.
Hay tres tipos de problemas en el retroceso:
- Problema de decisión: en este, buscamos una solución factible.
- Problema de optimización: en esto, buscamos la mejor solución.
- Problema de enumeración: en este, encontramos todas las soluciones factibles.
¿Cómo determinar si un problema se puede resolver usando Backtracking?
En general, todo problema de satisfacción de restricciones que tenga restricciones claras y bien definidas sobre cualquier solución objetiva, que construya de forma incremental un candidato a la solución y lo abandone («retrocede») tan pronto como determine que el candidato no puede completarse hasta una solución válida. solución, puede ser resuelto por Backtracking. Sin embargo, la mayoría de los problemas que se discuten se pueden resolver utilizando otros algoritmos conocidos como la programación dinámica o los algoritmos codiciosos .en complejidad de tiempo logarítmica, lineal, lineal-logarítmica en orden de tamaño de entrada y, por lo tanto, eclipsa el algoritmo de retroceso en todos los aspectos (ya que los algoritmos de retroceso son generalmente exponenciales tanto en el tiempo como en el espacio). Sin embargo, aún quedan algunos problemas, que hasta ahora solo tienen algoritmos de retroceso para resolverlos.
Considere una situación en la que tiene tres cajas frente a usted y solo una de ellas tiene una moneda de oro, pero no sabe cuál. Entonces, para obtener la moneda, deberás abrir todas las cajas una por una. Primero marcarás la primera casilla, si no contiene la moneda, tendrás que cerrarla y marcar la segunda casilla y así sucesivamente hasta encontrar la moneda. Esto es backtracking, es decir, resolver todos los subproblemas uno por uno para llegar a la mejor solución posible.
Considere el siguiente ejemplo para entender el enfoque de Backtracking más formalmente,
Dada una instancia de cualquier problema computacional ![]() y los datos
y los datos ![]() correspondientes a la instancia, todas las restricciones que deben cumplirse para resolver el problema están representadas por
correspondientes a la instancia, todas las restricciones que deben cumplirse para resolver el problema están representadas por ![]() . Un algoritmo de retroceso funcionará de la siguiente manera:
. Un algoritmo de retroceso funcionará de la siguiente manera:
El algoritmo comienza a construir una solución, comenzando con un conjunto de soluciones vacío ![]() . S = {}
. S = {}
- Suma al primer movimiento que aún queda (Todos los movimientos posibles se agregan
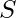 uno por uno). Esto ahora crea un nuevo subárbol
uno por uno). Esto ahora crea un nuevo subárbol 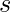 en el árbol de búsqueda del algoritmo.
en el árbol de búsqueda del algoritmo. - Compruebe si
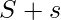 satisface cada una de las restricciones en
satisface cada una de las restricciones en 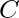 .
.
- En caso afirmativo, entonces el subárbol
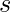 es «elegible» para agregar más «hijos».
es «elegible» para agregar más «hijos». - De lo contrario, todo el subárbol
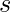 es inútil, por lo que vuelve al paso 1 usando argument
es inútil, por lo que vuelve al paso 1 usando argument 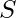 .
.
- En caso afirmativo, entonces el subárbol
- En caso de «elegibilidad» del subárbol recién formado
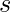 , vuelve al paso 1, usando el argumento
, vuelve al paso 1, usando el argumento 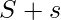 .
. - Si la comprobación
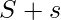 devuelve que es una solución para todos los datos
devuelve que es una solución para todos los datos 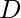 . Salida y terminación del programa.
. Salida y terminación del programa.
De lo contrario, devuelva que no es posible una solución con la corriente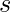 y, por lo tanto, deséchelo.
y, por lo tanto, deséchelo.
Diferencia entre recursividad y retroceso:
En recursión, la función se llama a sí misma hasta que llega a un caso base. Al retroceder, usamos la recursividad para explorar todas las posibilidades hasta obtener el mejor resultado para el problema.
Pseudocódigo para retroceder :
1. Solución recursiva de retroceso.
void findSolutions(n, other params) :
if (found a solution) :
solutionsFound = solutionsFound + 1;
displaySolution();
if (solutionsFound >= solutionTarget) :
System.exit(0);
return
for (val = first to last) :
if (isValid(val, n)) :
applyValue(val, n);
findSolutions(n+1, other params);
removeValue(val, n);
2. Averiguar si existe o no una solución
boolean findSolutions(n, other params) :
if (found a solution) :
displaySolution();
return true;
for (val = first to last) :
if (isValid(val, n)) :
applyValue(val, n);
if (findSolutions(n+1, other params))
return true;
removeValue(val, n);
return false;
Intentemos resolver un problema de retroceso estándar, el problema de N-Queen .
La Reina N es el problema de colocar N reinas de ajedrez en un tablero de ajedrez N × N para que no haya dos reinas que se ataquen entre sí. Por ejemplo, la siguiente es una solución para el problema de 4 Queen.

El resultado esperado es una array binaria que tiene unos para los bloques donde se colocan las reinas. Por ejemplo, a continuación se muestra la array de salida para la solución anterior de 4 reinas.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Algoritmo de retroceso : la idea es colocar las reinas una por una en diferentes columnas, comenzando desde la columna más a la izquierda. Cuando colocamos una reina en una columna, buscamos conflictos con reinas ya colocadas. En la columna actual, si encontramos una fila para la que no hay conflicto, marcamos esta fila y columna como parte de la solución. Si no encontramos esa fila debido a conflictos, retrocedemos y devolvemos falso.
Algoritmos de retroceso:
- Genera strings k-arias
- Problema de coloración de gráficos
- ciclos hamiltonianos
- Problema de N-Queens
- Problema de mochila
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column. Do following for every tried row.
a) If the queen can be placed safely in this row then mark this [row,
column] as part of the solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to a solution then return
true.
c) If placing queen doesn't lead to a solution then unmark this [row,
column] (Backtrack) and go to step (a) to try other rows.
4) If all rows have been tried and nothing worked, return false to trigger
backtracking.
Puede consultar el artículo sobre Backtracking | Conjunto 3 (N Problema de la Reina) para la implementación completa del enfoque anterior.
Más problemas de retroceso :
Publicación traducida automáticamente
Artículo escrito por AayushChaturvedi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA