Rompecabezas 29 | (Rompecabezas de rueda de coche)

Rompecabezas : Un coche tiene 4 neumáticos y 1 neumático de repuesto. Cada neumático puede recorrer una distancia máxima de 20 000 millas antes de desgastarse. ¿Cuál es la distancia máxima que puede recorrer el automóvil antes de verse obligado a comprar una llanta nueva? Puede cambiar los neumáticos (utilizando el neumático de repuesto) un número ilimitado de veces. 
 

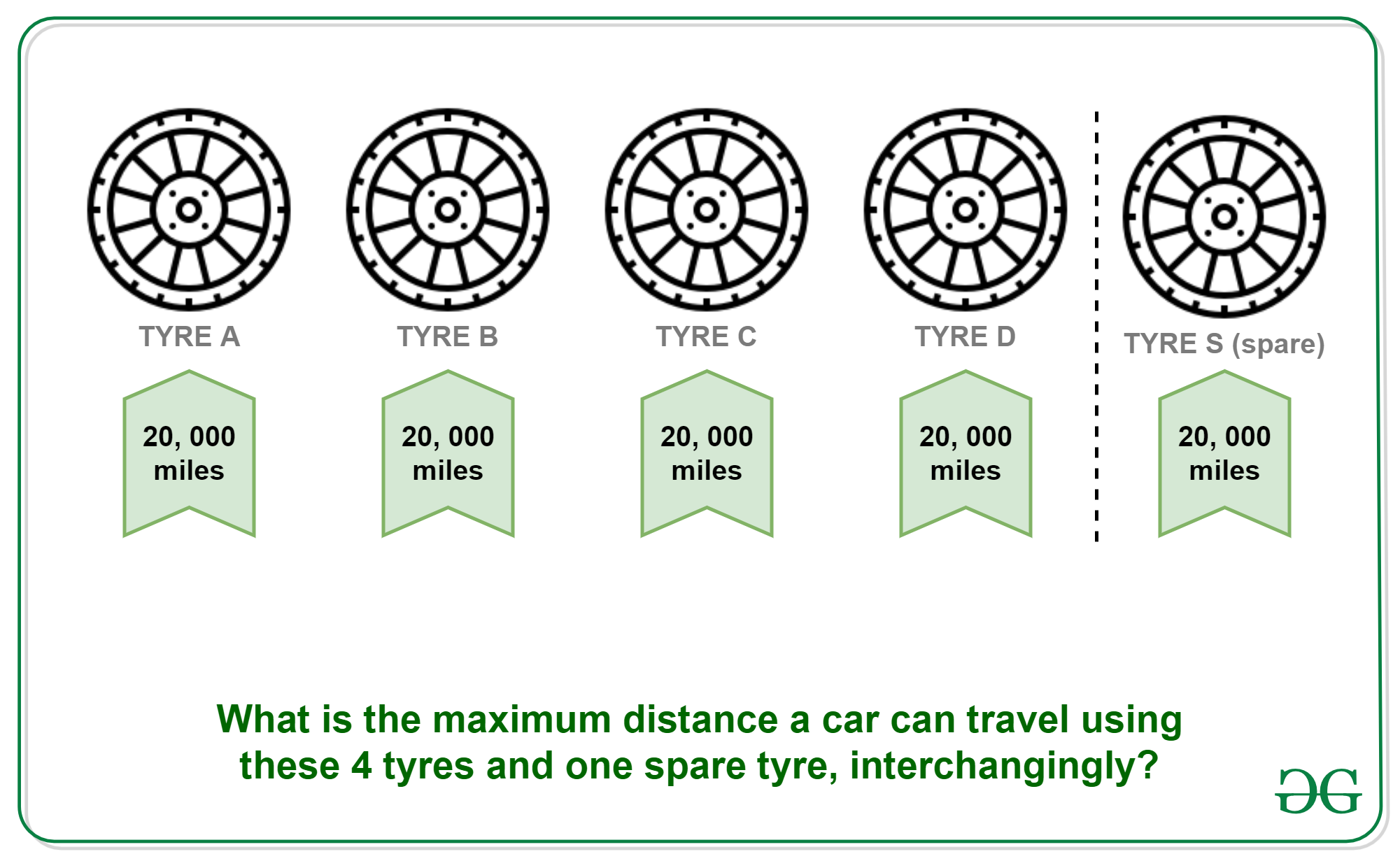
Respuesta : 25000 kms
Solución : divida la vida útil de la llanta de refacción en 4 partes iguales, es decir, 5000 y cámbiela cada vez que complete una distancia de 5000 millas. 
Sean cuatro llantas A, B, C y D y la llanta de refacción S.
 

• 5000 KM: Reemplace A con S. Distancias restantes (A, B, C, D, S): 15000, 15000, 15000, 15000, 20000. 
   

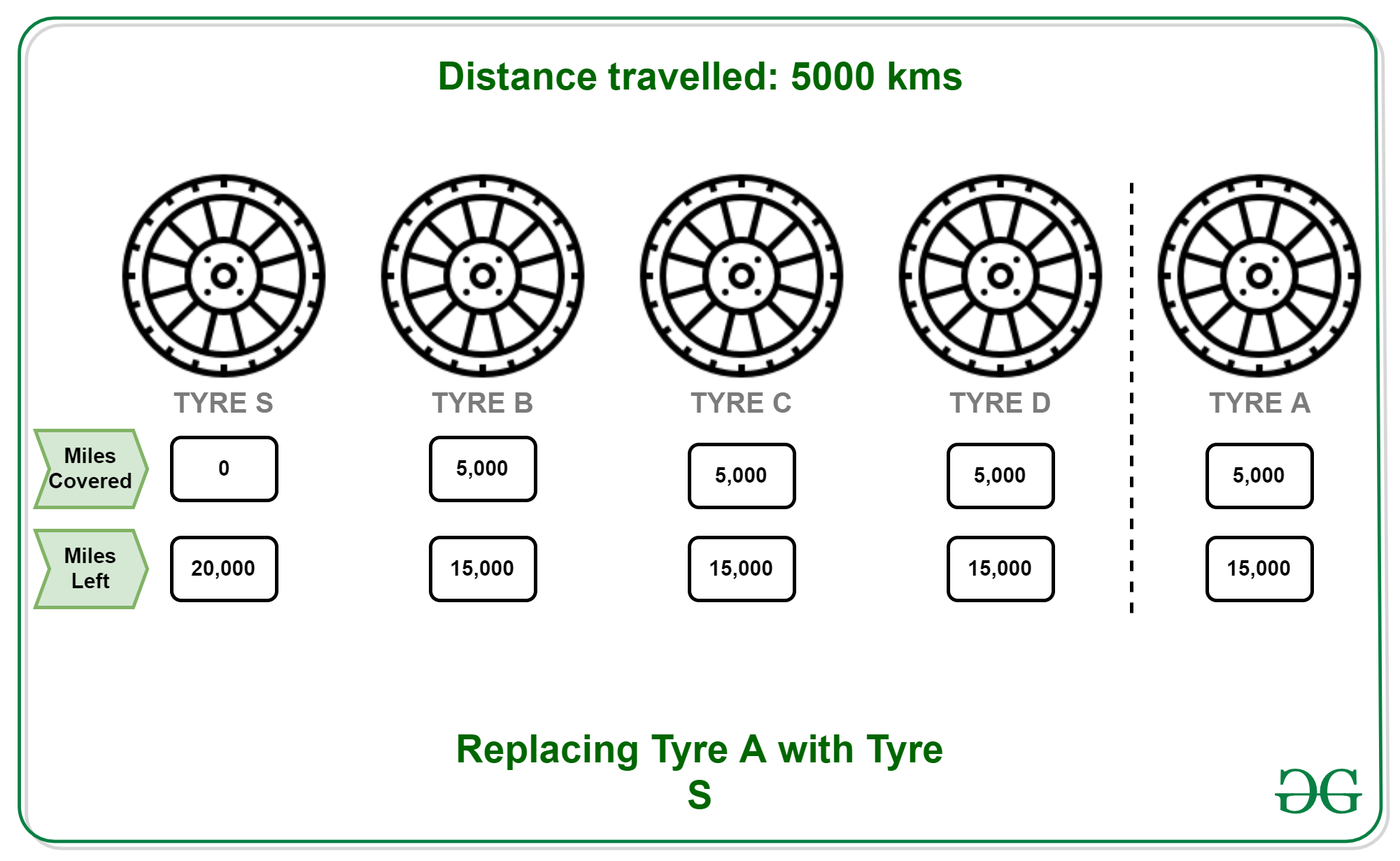
• 10000 KMs: Vuelva a colocar A en su posición original y reemplace B por S. Distancias restantes (A, B, C, D, S): 15000, 10000, 10000, 10000, 15000. 
   

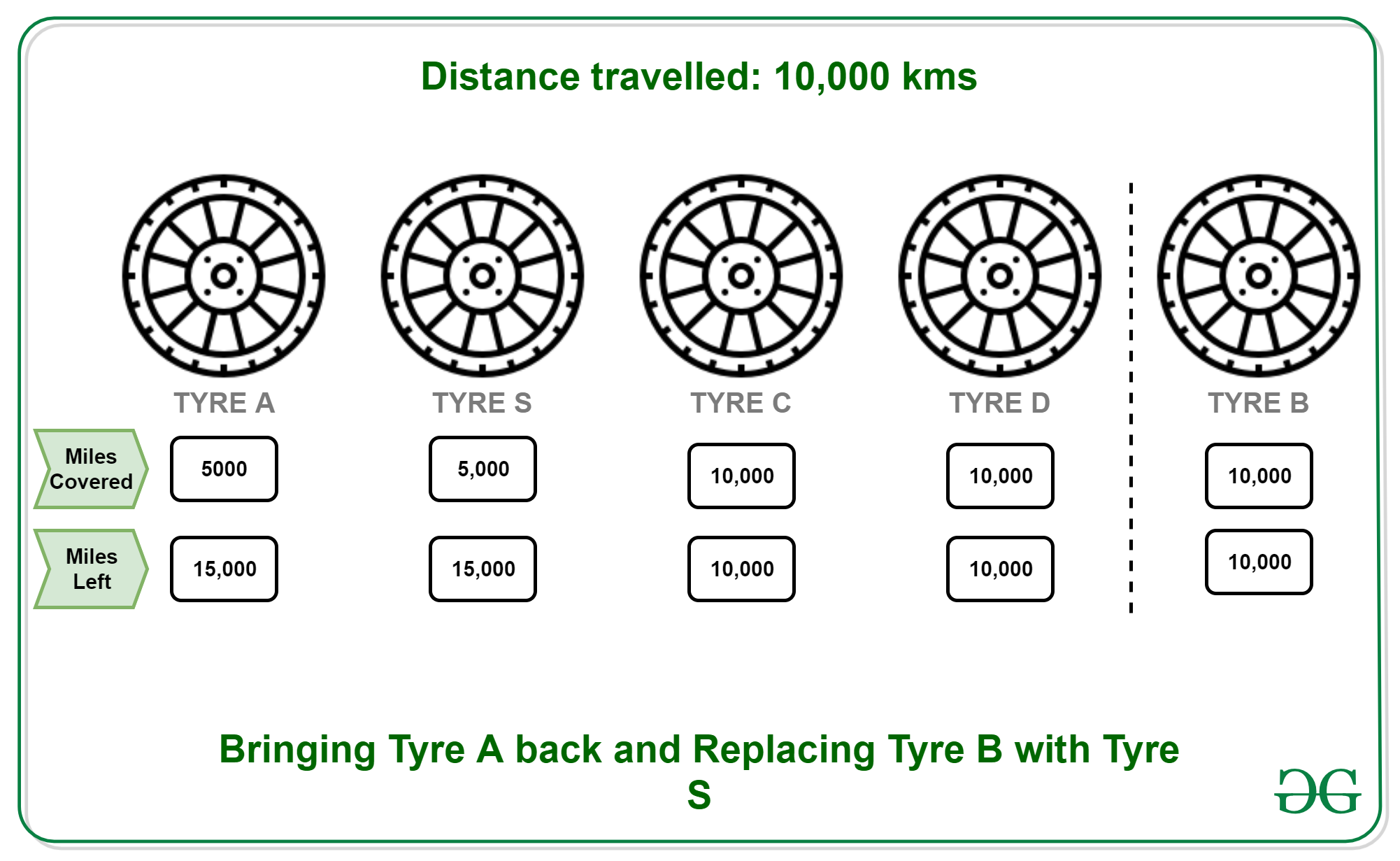
• 15000 KMs: Vuelva a colocar B en su posición original y reemplace C con S. Distancias restantes (A, B, C, D, S): 10000, 10000, 5000, 5000, 10000. 
   

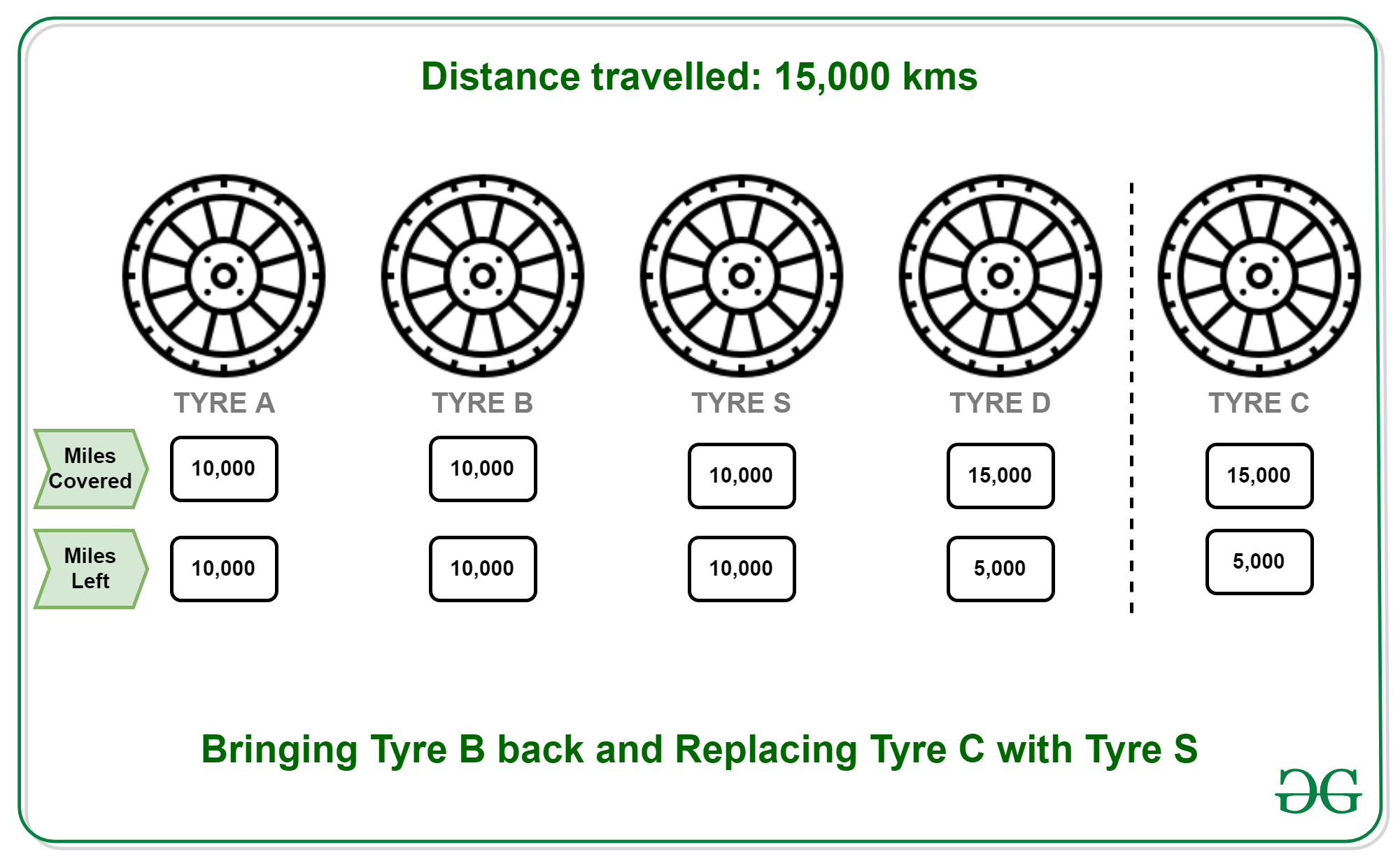
• 20000 KMs: Vuelva a colocar C en su posición original y reemplace D con S. Distancias restantes (A, B, C, D, S): 5000, 5000, 5000, 0, 5000. 
   

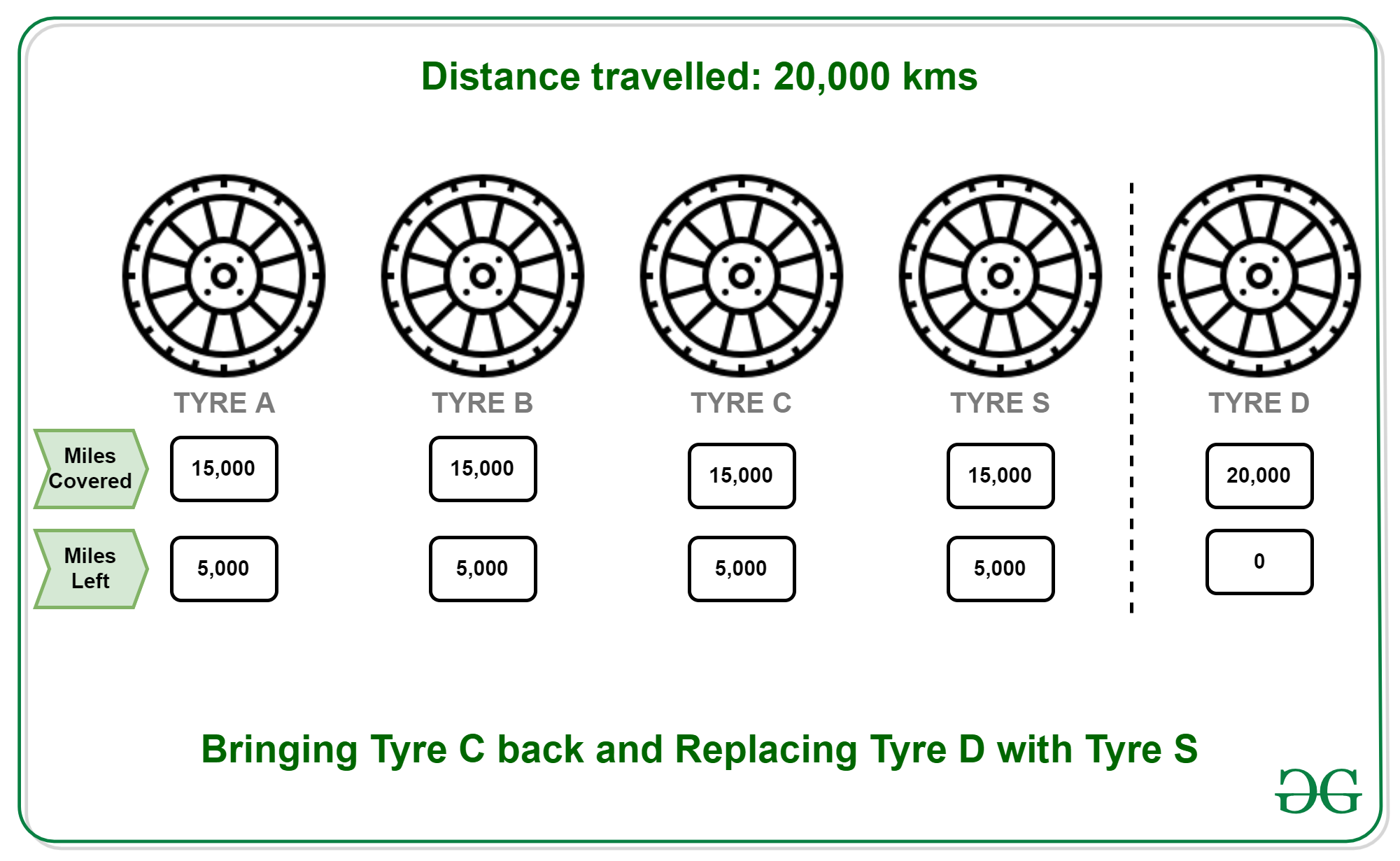
• 25000 KM: Todos los neumáticos ahora están completamente desgastados. 
   

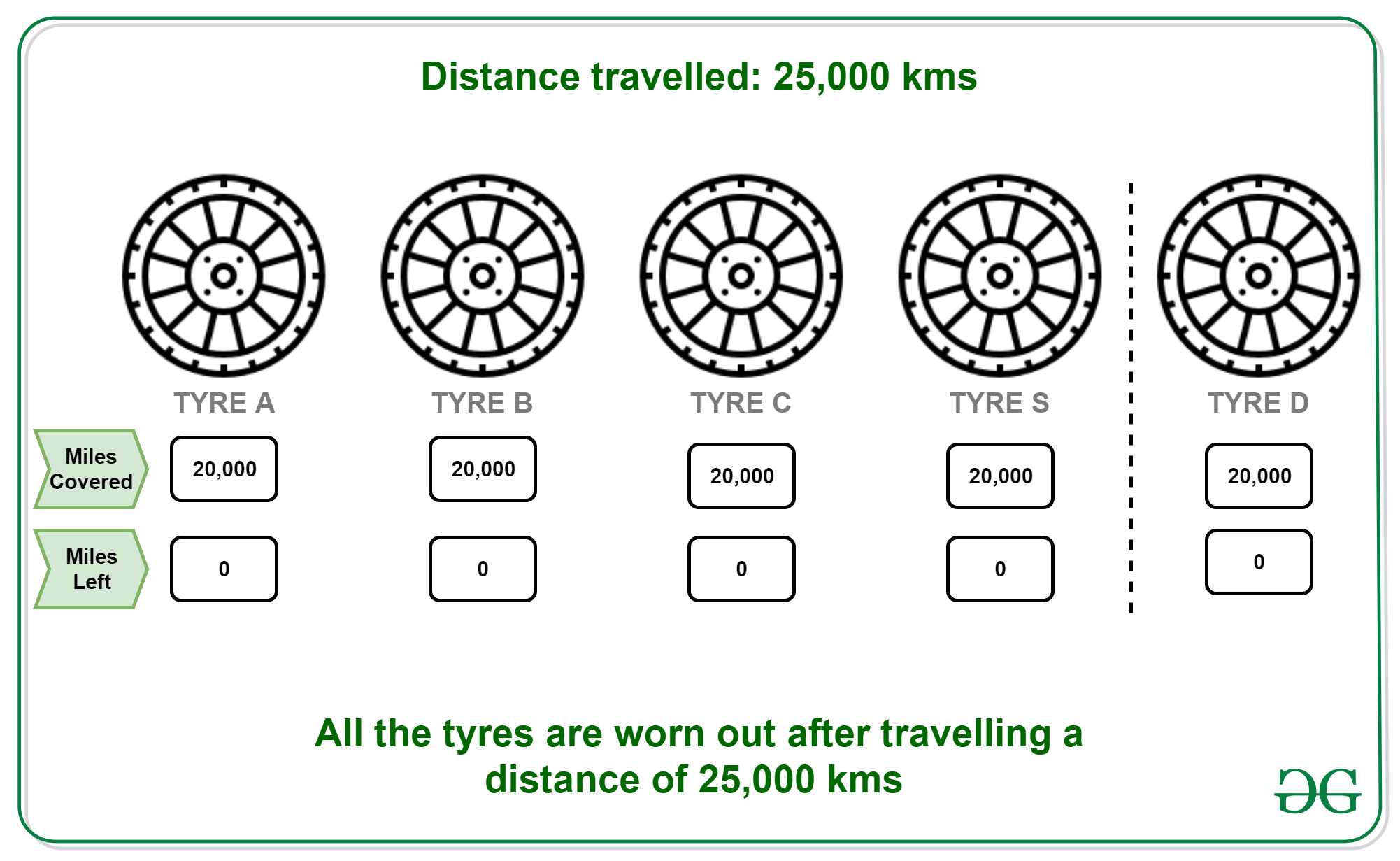
Todos los neumáticos se utilizan en toda su fuerza. 
 

Pregunta de entrevista de Amazon relacionada

Hay n lápices, cada uno de l de largo. Cada uno puede escribir 4 kilómetros. Después de escribir 4 kilómetros tiene l/4 de longitud. Se pueden juntar 4 lápices que tengan 1/4 de largo y se puede hacer 1 lápiz. Uno no puede hacer un lápiz de piezas si las piezas restantes son 3 o 2 o 1 en número, pero uno puede incluir estas piezas restantes cuando sea necesario. 
Escribe una relación independiente de l, longitud del lápiz dado, para cuánto se puede escribir con n lápices. 
Ejemplos: 
 

Input: 4
Output: 20

Enfoque recursivo: 
supongamos que usamos 3 lápices que serán 12 y generarán 3 lápices usados, ahora si los lápices restantes son mayores que cero, al menos 1 lápiz sin usar se puede usar con esos 3 sin usar para escribir 4 y eso generará 1 lápiz más sin usar. Esto se seguirá repitiendo.
 

if(n-3 >= 1){
  f(n) = f(n-3) + 12 + 4
} 
else{
  // Used pencil that cannot be used
  f(n) = 4*n
}

A continuación se muestra la implementación del enfoque anterior:
 

int count(int n)
{
    if (n < 4) {
        return (n * 4);
    }
    else {
        return (16 + count(n - 3));
    }
}

Enfoque matemático O(1): 
la relación anterior se puede optimizar en O(1)
 

// x is max no of time we can 
//subtract 3 without n-3 <= 3
n - 3*x <= 3     
x  >  (n-3)/3
i.e. n/3 - 1 if it divides exactly
else n/3

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find relation independent of l
// length of the given pencil, for how much one
// can write from n pencils.
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find no of pencils
int count(int n)
{
    int x = (n / 3) - 1;
    if (n % 3) {
        x++;
    }
    return (4 * x + 4 * n);
}
 
// Driver function
int main()
{
    int n = 5;
    cout << count(n) << endl;
}

// Java program to find relation independent of l
// length of the given pencil, for how much one
// can write from n pencils.
class GFG
{
 
// Function to find no of pencils
static int count(int n)
{
    int x = (n / 3) - 1;
    if (n % 3 > 0)
    {
        x++;
    }
    return (4 * x + 4 * n);
}
 
// Driver code
public static void main(String[] args)
{
    int n = 5;
    System.out.print(count(n) +"\n");
}
}
 
// This code is contributed by PrinciRaj1992

# Python3 program to find relation independent of l
# length of the given pencil, for how much one
# can write from n pencils.
 
# Function to find no of pencils
def count(n):
    x = (n // 3) - 1;
    if (n % 3 > 0):
        x+=1;
     
    return (4 * x + 4 * n);
 
# Driver code
if __name__ == '__main__':
    n = 5;
    print(count(n));
     
# This code is contributed by PrinciRaj1992

// C# program to find relation independent of l
// length of the given pencil, for how much one
// can write from n pencils.
using System;
 
class GFG
{
 
// Function to find no of pencils
static int count(int n)
{
    int x = (n / 3) - 1;
    if (n % 3 > 0)
    {
        x++;
    }
    return (4 * x + 4 * n);
}
 
// Driver code
public static void Main(String[] args)
{
    int n = 5;
    Console.Write(count(n) +"\n");
}
}
 
// This code is contributed by 29AjayKumar

<script>
// Javascript program to find relation independent of l
// length of the given pencil, for how much one
// can write from n pencils.
 
// Function to find no of pencils
function count(n)
{
    let x = Math.floor(n / 3) - 1;
    if (n % 3 > 0)
    {
        x++;
    }
    return (4 * x + 4 * n);
}
 
// Driver code
let n = 5;
document.write(count(n) +"<br>");
 
// This code is contributed by rag2127
</script>

24