Rompecabezas 64 | Rodea los Pueblos

En un distrito llamado Daulatpur, que es una de las ciudades mejor planificadas del mundo, hay una cierta disposición de las aldeas. El arreglo se adhiere a los siguientes patrones de diseño:

• Todos los límites de un pueblo son rectos, y todos los pueblos están rodeados por cuatro límites de la misma longitud.
• La longitud de la línea que une los puntos no adyacentes es igual.
• Todos los pueblos están divididos en un grupo de tres pueblos, con un patio de recreo común completamente rodeado por un límite de cada pueblo.

Luego, los pueblos se clasifican aún más en la categoría de pueblos especiales. Los pueblos especiales tienen la propiedad de que el área de uno de los pueblos de su grupo es igual a la suma del área de los otros dos pueblos. Se le ha dicho que los límites de un pueblo pueden variar de 1 km a 15 km de longitud.
Averigüe la suma del área de los patios de recreo para ese grupo de pueblos que se han categorizado en pueblos especiales.

Nota: Se da que para cada conjunto de límites de los pueblos, solo existe un grupo especial.

Solución: 114 Km^2 .

Explicación: En la pregunta anterior se da que los límites de los pueblos son rectos, iguales y en número de cuatro. La longitud de la línea que une los puntos no adyacentes => la longitud de la diagonal del polígono. Como los lados y las diagonales del polígono son iguales, esto implica que el polígono es un cuadrado. Entonces, todo el distrito es una colección de trillizos dados de pueblos, donde el área entre las plazas es el patio de recreo.

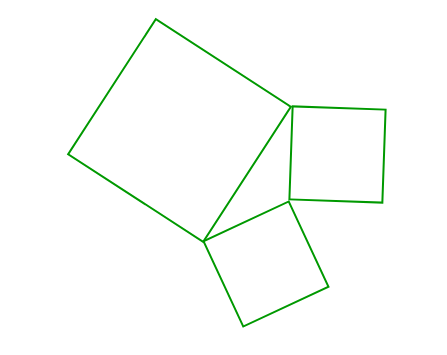
Ahora, la pregunta dice que los pueblos especiales son aquellos pueblos que tienen la suma de áreas de dos igual a la tercera. Deje que el lado de los pueblos en un triplete sea a, b y c respectivamente, lo que implica que
a^2 = b^2 + c^2

• Ahora, del 1 al 15 tienes que encontrar los tripletes pitagóricos que son (3, 4, 5), (5, 12, 13), (9, 12, 15) y (6, 8, 10) respectivamente.
• Como a ^ 2 = b ^ 2 + c ^ 2, los patios de recreo triangulares tienen un ángulo recto. Y como solo hay uno de esos grupos especiales.
• Por tanto, la respuesta es (1/2 ) x 3 x 4 + (1/2) x 5 x 12 + (1/2) x 6 x 8 + (1/2) x 9 x 12= 114 .

Este rompecabezas es aportado por Praveer Satyam. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.