Rompecabezas 67 | Triángulo de ajuste

Sameer le hace una pregunta a su amigo Kartik para poner a prueba su inteligencia. 

Sameer – Te han dado un triángulo rectángulo ABC, con ángulo recto en B. La longitud de la hipotenusa es de 10 m y la altura a la hipotenusa desde B es de 6 m. 

Kartik- Vamos. 

Sameer – Dime el área del triángulo ABC. 

Kartik – 30 metros cuadrados. 

Sameer – Sabía que dirías esto, pero te equivocas amigo. Prueba algo de geometría. 

Kartik necesita tu ayuda para responder a esta pregunta. 
 

Respuesta: Tal triángulo nunca puede existir  .

Solución: Al principio parecería que 30 metros cuadrados es la respuesta correcta, usando la fórmula 

0.5*Base*Altura 
=0.5*10*6 
=30 

Un triángulo con dimensiones dadas nunca puede existir. La altura máxima a la hipotenusa de un triángulo puede ser la mitad de la longitud de la hipotenusa. (Ver foto) 

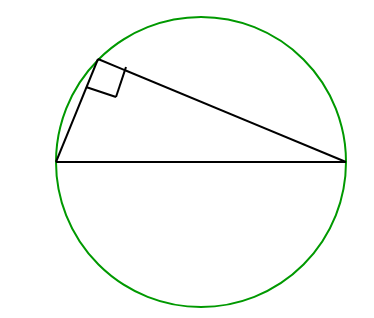
Entonces, la altura máxima puede ser la mitad del diámetro, que en este caso es de 10 m. Por tanto, la altura máxima a la hipotenusa puede ser la mitad de 10 m, es decir, sólo 5 m. 
 

Este rompecabezas es aportado por Feroz Baig. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.