Rompecabezas: a continuación se muestra un rompecabezas de cerillas, mueva 3 cerillas para obtener 3 cuadrados . Dé todas las posibles soluciones únicas para el problema dado.

Solución:
Analicemos una solución paso a paso para llegar a un resultado.
1. Cuente el número total de fósforos disponibles en el problema. En la figura, el número total de fósforos es igual a 12, como se muestra en la siguiente figura.

2. Ahora para hacer un cuadrado se usan 4 palos entonces, para formar 4 cuadrados se hubieran usado 16 palos pero solo tenemos 12 palos. Aquí viene el concepto de palos comunes entre dos formas unitarias adyacentes.

Los palos 5,4,6,10 son fósforos comunes
3. Ahora para hacer 3 cuadrados se requieren 4 * 3 = 12 palos (como máximo, cuando los palos no son comunes entre los cuadrados). Y en este caso, hay 12 fósforos disponibles. Ahora, todo lo que tenemos que hacer es-
- Elimina los 4 palos comunes.
- Forma 3 cuadrados independientes,
- Moviendo solo 3 palos.
4. Concepto de palo prometedor
- Curiosamente, si cualquiera de los 12 palos se mueve primero, al menos dos palos comunes perderán sus propiedades comunes. Al mover cualquiera de los cuatro palos comunes, inmediatamente se producirán 4 palos independientes. Esto es imposible de lograr en los dos movimientos restantes. Por lo tanto, el primer movimiento de palo eliminando dos palos comunes no puede ser un palo común.
- Ocho de los palos restantes (1, 2, 3, 12, 11, 9, 8, 7) se pueden mover primero, ya que los 8 palos comparten la misma posición, función y ubicación dentro de la estructura. Estos son los palos de esquina. Estos son los palos prometedores.
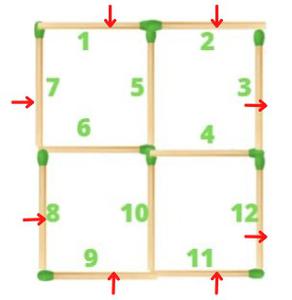
Los palos marcados son palos prometedores.
Solución 1: técnica común de eliminación de palos
El número 4 no se puede dividir en tres enteros positivos con un valor mínimo de 1. Uno de los tres números tiene que ser 2. Al aplicar Razonamiento , se pueden eliminar 4 palos comunes en solo 3 movimientos como-
1. Mueva primero el palo número 2. Esto destruye 1 cuadrado y elimina 2 cerillas comunes.

2. Mueva el palo numerado 3. Esto da como resultado dos palos gratis ganados, dos palos comunes eliminados (como 5, 4 no son palos comunes ahora) y 1 casilla reducida.

3. Mueva el tercer palo de manera que elimine 2 palos comunes más y destruya 1 cuadrado más.
Nota:
Cualquiera de los cuatro palos numerados 1,7,11,12 pertenecientes a los dos cuadrados adyacentes al cuadrado destruido en este momento no se puede quitar, ya que eliminaría 1 palo común más, destruiría 1 cuadrado más, sin embargo, crearía dos palos sin colocar. y la situación podría ser imposible de manipular.
La única solución factible para este paso es seleccionar el palo 8.

Se forman 3 cuadrados
Por lo tanto , se pueden concluir 3 soluciones más mediante este método, como se muestra.
Solución 2: si se consideran los palos 1,7,12 para el movimiento en lugar de 2,3,8 en la primera solución.

Solución 3: Si se consideran los palos 1,7,11 para el movimiento en lugar de 2,3,8 en la primera solución.

Solución 4: si se consideran los palos 8,9,2 para el movimiento en lugar de 2,3,8 en la primera solución.

Publicación traducida automáticamente
Artículo escrito por ninja_hattori y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA