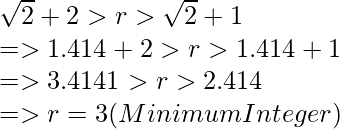Se requiere una string binaria de tamaño mínimo tal que la probabilidad de eliminar dos 1 al azar sea 1/X

Dado un valor X , la tarea es encontrar una string binaria de tamaño mínimo, de modo que si se eliminan 2 caracteres al azar, la probabilidad de que ambos caracteres sean ‘1’ es 1/X . Imprime el tamaño de dicha string binaria.

Ejemplo:

Entrada: X = 2 
Salida: 4 
Explicación: 
Sea la string binaria “0111”. 
La probabilidad de elegir 2 1 de la string dada es = 3C2 / 4C2 = 3/6 = 1/2 (que es igual a 1/X). 
Por lo tanto, el tamaño requerido es 4. 
(Para este ejemplo, se puede tomar cualquier string binaria de 4 tamaños con 3 ‘1’ y 1 ‘0’).
Entrada: X = 8 
Salida: 5 

Planteamiento: Intentaremos encontrar una fórmula para resolver este problema.  

Sea 
r = número de 1 en la string 
y 
b = número de 0 en la string.

• Si se eliminan dos caracteres al azar, entonces 

 Número total de vías = (r + b) _{C 2.} 

• Si se desea que 2 caracteres sean 1, Número favorable de casos = r _{C 2} . 
   
• Por lo tanto, P(ambos son 1) = r _C2 / (r + b) _C2 . 
  
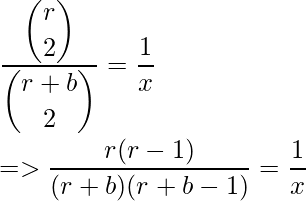
• Una observación engañosa para seguir adelante con nuestro cálculo es: 
  
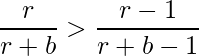
• Elevando al cuadrado la desigualdad y comparando con la igualdad, obtenemos 
  
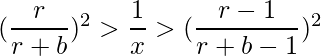
• Si r > 1, sacamos raíz cuadrada en los 3 lados. 
  
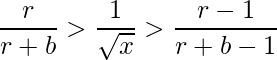
• Tomando la parte más a la izquierda de la desigualdad, obtenemos:  
  
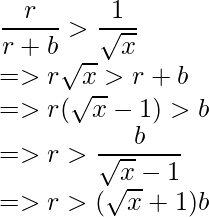
• De manera similar, tomando la parte más a la derecha de la desigualdad, obtenemos:  
  
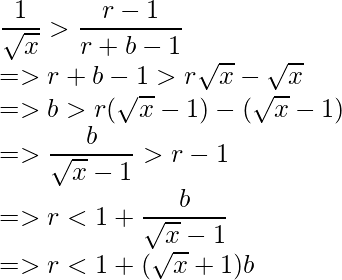
• Combinando las conclusiones derivadas, obtenemos el rango de r en términos de b.  
  
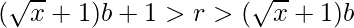
• Para el valor mínimo de string, establecemos b = 1  
  
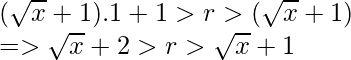
• Para obtener un r mínimo válido, tomamos el primer valor entero de r en este rango.

Por ejemplo: si X = 2
 

 

Por lo tanto, r = 3 yb = 1 . 
P(ambos caracteres son 1) = 3C2 / 4C2 = 2/4 = 1/2 

A continuación se muestra la implementación del enfoque anterior.

// C++ implementation of the
// above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function returns the minimum
// size of the string
int MinimumString(int x)
{
    // From formula
    int b = 1;
 
    // Left limit of r
    double left_lim = sqrt(x) + 1.0;
 
    // Right limit of r
    double right_lim = sqrt(x) + 2.0;
 
    int r;
    for (int i = left_lim; i <= right_lim; i++) {
        if (i > left_lim and i < right_lim) {
            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
 
    return b + r;
}
 
// Driver Code
int main()
{
 
    int X = 2;
    cout << MinimumString(X);
    return 0;
}

// Java implementation of the
// above approach
import java.util.*;
 
class GFG{
 
// Function returns the minimum
// size of the String
static int MinimumString(int x)
{
     
    // From formula
    int b = 1;
 
    // Left limit of r
    double left_lim = Math.sqrt(x) + 1.0;
 
    // Right limit of r
    double right_lim = Math.sqrt(x) + 2.0;
 
    int r = 0;
    for(int i = (int)left_lim; i <= right_lim; i++)
    {
        if (i > left_lim && i < right_lim)
        {
             
            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}
 
// Driver Code
public static void main(String[] args)
{
    int X = 2;
    System.out.print(MinimumString(X));
}
}
 
// This code is contributed by PrinciRaj1992

# Python3 implementation of
# the above approach
from math import sqrt
 
# Function returns the minimum
# size of the string
def MinimumString(x):
 
    # From formula
    b = 1
 
    # Left limit of r
    left_lim = sqrt(x) + 1.0
 
    # Right limit of r
    right_lim = sqrt(x) + 2.0
 
    for i in range(int(left_lim),
                   int(right_lim) + 1):
        if(i > left_lim and i < right_lim):
             
            # Smallest integer in
            # the valid range
            r = i
            break
 
    return b + r
 
# Driver Code
if __name__ == '__main__':
 
    X = 2
 
    print(MinimumString(X))
 
# This code is contributed by Shivam Singh

// C# implementation of the
// above approach
using System;
 
class GFG{
 
// Function returns the minimum
// size of the String
static int MinimumString(int x)
{
     
    // From formula
    int b = 1;
 
    // Left limit of r
    double left_lim = Math.Sqrt(x) + 1.0;
 
    // Right limit of r
    double right_lim = Math.Sqrt(x) + 2.0;
 
    int r = 0;
    for(int i = (int)left_lim; i <= right_lim; i++)
    {
        if (i > left_lim && i < right_lim)
        {
             
            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}
 
// Driver Code
public static void Main(String[] args)
{
    int X = 2;
     
    Console.Write(MinimumString(X));
}
}
 
// This code is contributed by gauravrajput1

<script>
 
// Javascript program for
// the above approach
    
// Function returns the minimum
// size of the String
function MinimumString(x)
{
       
    // From formula
    let b = 1;
   
    // Left limit of r
    let left_lim = Math.sqrt(x) + 1.0;
   
    // Right limit of r
    let right_lim = Math.sqrt(x) + 2.0;
   
    let r = 0;
    for(let i = Math.floor(left_lim); i <= Math.floor(right_lim); i++)
    {
        if (i > left_lim && i < right_lim)
        {
               
            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}
     
// Driver Code
     
     let  X = 2;
    document.write(MinimumString(X));
 
</script>

4

Complejidad Temporal: O(1), ya que la diferencia entre el límite izquierdo y el límite derecho será siempre menor que 1. 
Espacio Auxiliar: O(1)