Dados dos enteros m & n, encuentre el número de secuencias posibles de longitud n tales que cada uno de los siguientes elementos sea mayor o igual que el doble del elemento anterior pero menor o igual que m.
Ejemplos:
Input : m = 10, n = 4
Output : 4
There should be n elements and value of last
element should be at-most m.
The sequences are {1, 2, 4, 8}, {1, 2, 4, 9},
{1, 2, 4, 10}, {1, 2, 5, 10}
Input : m = 5, n = 2
Output : 6
The sequences are {1, 2}, {1, 3}, {1, 4},
{1, 5}, {2, 4}, {2, 5}
Según la condición dada, el valor n-ésimo de la secuencia puede ser como máximo m. Puede haber dos casos para el elemento n-ésimo:
- Si es m, entonces el (n-1)-ésimo elemento es como máximo m/2. Recurrimos para m/2 y n-1.
- Si no es m, entonces a lo sumo es m-1. Recurrimos para (m-1) y n.
El número total de secuencias es la suma del número de secuencias que incluye m y el número de secuencias donde m no está incluido. Por lo tanto, el problema original de encontrar el número de secuencias de longitud n con valor máximo m se puede subdividir en subproblemas independientes de encontrar el número de secuencias de longitud n con valor máximo m-1 y el número de secuencias de longitud n-1 con valor máximo m/ 2.
C++
// C++ program to count total number
// of special sequences of length n where
#include <iostream>
using namespace std;
// Recursive function to find the number of special
// sequences
int getTotalNumberOfSequences(int m, int n)
{
// A special sequence cannot exist if length
// n is more than the maximum value m.
if (m < n)
return 0;
// If n is 0, found an empty special sequence
if (n == 0)
return 1;
// There can be two possibilities : (1) Reduce
// last element value (2) Consider last element
// as m and reduce number of terms
return getTotalNumberOfSequences(m - 1, n) +
getTotalNumberOfSequences(m / 2, n - 1);
}
// Driver code
int main()
{
int m = 10;
int n = 4;
cout << "Total number of possible sequences "
<< getTotalNumberOfSequences(m, n);
return 0;
}
// This code is contributed by shivanisinghss2110
Java
// Java program to count total number
// of special sequences of length n where
class Sequences
{
// Recursive function to find the number of special
// sequences
static int getTotalNumberOfSequences(int m, int n)
{
// A special sequence cannot exist if length
// n is more than the maximum value m.
if(m < n)
return 0;
// If n is 0, found an empty special sequence
if(n == 0)
return 1;
// There can be two possibilities : (1) Reduce
// last element value (2) Consider last element
// as m and reduce number of terms
return getTotalNumberOfSequences (m-1, n) +
getTotalNumberOfSequences (m/2, n-1);
}
// main function
public static void main (String[] args)
{
int m = 10;
int n = 4;
System.out.println("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
}
}
Python3
#Python3 program to count total number of
#special sequences of length n where
#Recursive function to find the number of
# special sequences
def getTotalNumberOfSequences(m,n):
#A special sequence cannot exist if length
#n is more than the maximum value m.
if m<n:
return 0
#If n is 0, found an empty special sequence
if n==0:
return 1
#There can be two possibilities : (1) Reduce
#last element value (2) Consider last element
#as m and reduce number of terms
res=(getTotalNumberOfSequences(m-1,n)+
getTotalNumberOfSequences(m//2,n-1))
return res
#Driver Code
if __name__=='__main__':
m=10
n=4
print('Total number of possible sequences:',getTotalNumberOfSequences(m,n))
#This code is contributed by sahilshelangia
C#
// C# program to count total number
// of special sequences of length n
// where every element is more than
// or equal to twice of previous
using System;
class GFG
{
// Recursive function to find
// the number of special sequences
static int getTotalNumberOfSequences(int m, int n)
{
// A special sequence cannot exist if length
// n is more than the maximum value m.
if(m < n)
return 0;
// If n is 0, found an empty special sequence
if(n == 0)
return 1;
// There can be two possibilities : (1) Reduce
// last element value (2) Consider last element
// as m and reduce number of terms
return getTotalNumberOfSequences (m-1, n) +
getTotalNumberOfSequences (m/2, n-1);
}
// Driver code
public static void Main ()
{
int m = 10;
int n = 4;
Console.Write("Total number of possible sequences " +
getTotalNumberOfSequences(m, n));
}
}
// This code is contributed by nitin mittal.
PHP
<?php
// PHP program to count total
// number of special sequences
// of length n where
// Recursive function to find
// the number of special sequences
function getTotalNumberOfSequences($m, $n)
{
// A special sequence cannot
// exist if length n is more
// than the maximum value m.
if ($m < $n)
return 0;
// If n is 0, found an empty
// special sequence
if ($n == 0)
return 1;
// There can be two possibilities :
// (1) Reduce last element value
// (2) Consider last element
// as m and reduce number of terms
return getTotalNumberOfSequences($m - 1, $n) +
getTotalNumberOfSequences($m / 2, $n - 1);
}
// Driver Code
$m = 10;
$n = 4;
echo("Total number of possible sequences ");
echo (getTotalNumberOfSequences($m, $n));
// This code is contributed by nitin mittal.
?>
Javascript
<script>
// program to count total number of special sequences
// of length n where
// Recursive function to find the number of special
// sequences
function getTotalNumberOfSequences( m, n)
{
// A special sequence cannot exist if length
// n is more than the maximum value m.
if (m < n)
return 0;
// If n is 0, found an empty special sequence
if (n == 0)
return 1;
// There can be two possibilities : (1) Reduce
// last element value (2) Consider last element
// as m and reduce number of terms
return getTotalNumberOfSequences (m-1, n) +
getTotalNumberOfSequences (m/2, n-1);
}
// Driver Code
let m = 10;
let n = 4;
document.write ("Total number of possible sequences ",
getTotalNumberOfSequences(m, n));
// This code is contributed by anikakapoor.
</script>
Producción:
Total number of possible sequences 4
Análisis de Complejidad:
Complejidad temporal: O(2 m ) en el peor de los casos
Complejidad espacial: O(m), la profundidad del árbol de recurrencia es m en el peor de los casos.
Tenga en cuenta que la función anterior calcula los mismos subproblemas una y otra vez. Considere el siguiente árbol para f(10, 4).
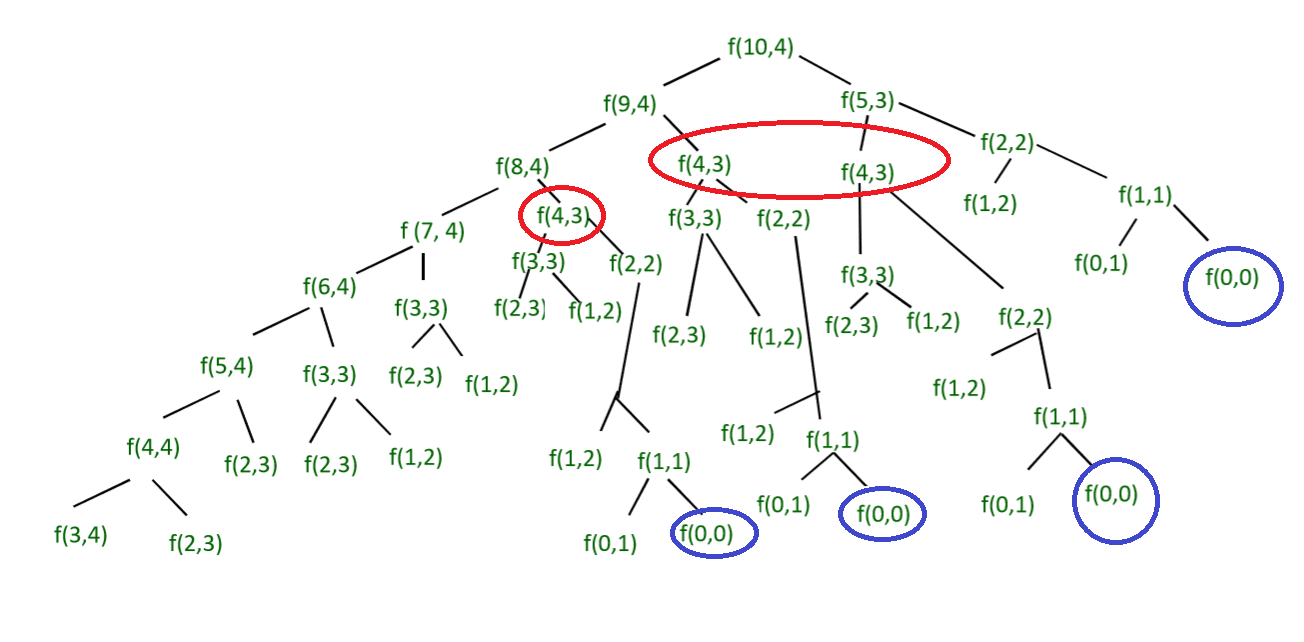
Árbol recursivo para m= 10 y N =4
Podemos resolver este problema usando programación dinámica.
C++
// C program to count total number of special sequences
// of length N where
#include <stdio.h>
// DP based function to find the number of special
// sequences
int getTotalNumberOfSequences(int m, int n)
{
// define T and build in bottom manner to store
// number of special sequences of length n and
// maximum value m
int T[m+1][n+1];
for (int i=0; i<m+1; i++)
{
for (int j=0; j<n+1; j++)
{
// Base case : If length of sequence is 0
// or maximum value is 0, there cannot
// exist any special sequence
if (i == 0 || j == 0)
T[i][j] = 0;
// if length of sequence is more than
// the maximum value, special sequence
// cannot exist
else if (i < j)
T[i][j] = 0;
// If length of sequence is 1 then the
// number of special sequences is equal
// to the maximum value
// For example with maximum value 2 and
// length 1, there can be 2 special
// sequences {1}, {2}
else if (j == 1)
T[i][j] = i;
// otherwise calculate
else
T[i][j] = T[i-1][j] + T[i/2][j-1];
}
}
return T[m][n];
}
// Driver Code
int main()
{
int m = 10;
int n = 4;
printf("Total number of possible sequences %d",
getTotalNumberOfSequences(m, n));
return 0;
}
Java
// Efficient java program to count total number
// of special sequences of length n where
class Sequences
{
// DP based function to find the number of special
// sequences
static int getTotalNumberOfSequences(int m, int n)
{
// define T and build in bottom manner to store
// number of special sequences of length n and
// maximum value m
int T[][]=new int[m+1][n+1];
for (int i=0; i<m+1; i++)
{
for (int j=0; j<n+1; j++)
{
// Base case : If length of sequence is 0
// or maximum value is 0, there cannot
// exist any special sequence
if (i == 0 || j == 0)
T[i][j] = 0;
// if length of sequence is more than
// the maximum value, special sequence
// cannot exist
else if (i < j)
T[i][j] = 0;
// If length of sequence is 1 then the
// number of special sequences is equal
// to the maximum value
// For example with maximum value 2 and
// length 1, there can be 2 special
// sequences {1}, {2}
else if (j == 1)
T[i][j] = i;
// otherwise calculate
else
T[i][j] = T[i-1][j] + T[i/2][j-1];
}
}
return T[m][n];
}
// main function
public static void main (String[] args)
{
int m = 10;
int n = 4;
System.out.println("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
}
}
Python3
#Python3 program to count total number of
#special sequences of length N where
#DP based function to find the number
# of special sequence
def getTotalNumberOfSequences(m,n):
#define T and build in bottom manner to store
#number of special sequences of length n and
#maximum value m
T=[[0 for i in range(n+1)] for i in range(m+1)]
for i in range(m+1):
for j in range(n+1):
#Base case : If length of sequence is 0
# or maximum value is 0, there cannot
#exist any special sequence
if i==0 or j==0:
T[i][j]=0
#if length of sequence is more than
#the maximum value, special sequence
# cannot exist
elif i<j:
T[i][j]=0
# If length of sequence is 1 then the
# number of special sequences is equal
# to the maximum value
# For example with maximum value 2 and
# length 1, there can be 2 special
# sequences {1}, {2}
elif j==1:
T[i][j]=i
else:
T[i][j]=T[i-1][j]+T[i//2][j-1]
return T[m][n]
#Driver Code
if __name__=='__main__':
m=10
n=4
print('Total number of possible sequences ',getTotalNumberOfSequences(m, n))
#This code is contributed by sahilshelangia
C#
// Efficient C# program to count total number
// of special sequences of length n where
using System;
class Sequences {
// DP based function to find
// the number of special
// sequences
static int getTotalNumberOfSequences(int m, int n)
{
// define T and build in
// bottom manner to store
// number of special sequences
// of length n and maximum value m
int [,]T=new int[m + 1, n + 1];
for (int i = 0; i < m + 1; i++)
{
for (int j = 0; j < n + 1; j++)
{
// Base case : If length
// of sequence is 0
// or maximum value is
// 0, there cannot
// exist any special
// sequence
if (i == 0 || j == 0)
T[i, j] = 0;
// if length of sequence
// is more than the maximum
// value, special sequence
// cannot exist
else if (i < j)
T[i,j] = 0;
// If length of sequence is 1 then the
// number of special sequences is equal
// to the maximum value
// For example with maximum value 2 and
// length 1, there can be 2 special
// sequences {1}, {2}
else if (j == 1)
T[i,j] = i;
// otherwise calculate
else
T[i,j] = T[i - 1, j] + T[i / 2, j - 1];
}
}
return T[m,n];
}
// Driver Code
public static void Main ()
{
int m = 10;
int n = 4;
Console.WriteLine("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// PHP program to count total
// number of special sequences
// of length N where
// DP based function to find
// the number of special
// sequences
function getTotalNumberOfSequences($m, $n)
{
// define T and build in bottom
// manner to store number of
// special sequences of length
// n and maximum value m
$T = array(array());
for ($i = 0; $i < $m + 1; $i++)
{
for ($j = 0; $j < $n + 1; $j++)
{
// Base case : If length of
// sequence is 0 or maximum
// value is 0, there cannot
// exist any special sequence
if ($i == 0 or $j == 0)
$T[$i][$j] = 0;
// if length of sequence is
// more than the maximum value,
// special sequence cannot exist
else if ($i < $j)
$T[$i][$j] = 0;
// If length of sequence is
// 1 then the number of
// special sequences is equal
// to the maximum value
// For example with maximum
// value 2 and length 1, there
// can be 2 special sequences
// {1}, {2}
else if ($j == 1)
$T[$i][$j] = $i;
// otherwise calculate
else
$T[$i][$j] = $T[$i - 1][$j] +
$T[$i / 2][$j - 1];
}
}
return $T[$m][$n];
}
// Driver Code
$m = 10;
$n = 4;
echo "Total number of possible sequences ",
getTotalNumberOfSequences($m, $n);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// Efficient javascript program to count total number
// of special sequences of length n where
// DP based function to find the number of special
// sequences
function getTotalNumberOfSequences(m, n)
{
// define T and build in bottom manner to store
// number of special sequences of length n and
// maximum value m
let T = new Array(m+1);
for (let i=0; i<m+1; i++)
{
T[i] = new Array(n+1);
for (let j=0; j<n+1; j++)
{
// Base case : If length of sequence is 0
// or maximum value is 0, there cannot
// exist any special sequence
if (i == 0 || j == 0)
T[i][j] = 0;
// if length of sequence is more than
// the maximum value, special sequence
// cannot exist
else if (i < j)
T[i][j] = 0;
// If length of sequence is 1 then the
// number of special sequences is equal
// to the maximum value
// For example with maximum value 2 and
// length 1, there can be 2 special
// sequences {1}, {2}
else if (j == 1)
T[i][j] = i;
// otherwise calculate
else
T[i][j] = T[i-1][j] + T[parseInt(i/2, 10)][j-1];
}
}
return T[m][n];
}
let m = 10;
let n = 4;
document.write("Total number of possible sequences "+
getTotalNumberOfSequences(m, n));
// This code is contributed rameshtravel07.
</script>
Producción:
4
Tiempo Complejidad : O(mxn)
Espacio Auxiliar : O(mxn)
Este artículo es una contribución de Bahubali . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA