Shell sort es principalmente una variación de Insertion Sort . En la ordenación por inserción, movemos los elementos solo una posición hacia adelante. Cuando un elemento tiene que moverse mucho más adelante, hay muchos movimientos involucrados. La idea de ShellSort es permitir el intercambio de artículos lejanos. En Shell sort, hacemos que la array esté ordenada por h para un valor grande de h. Seguimos reduciendo el valor de h hasta que se convierte en 1. Se dice que una array está ordenada por h si todas las sublistas de cada h-ésimo elemento están ordenadas.
Algoritmo:
Paso 1 − Iniciar
Paso 2 − Inicializar el valor del tamaño del espacio. Ejemplo: h
Paso 3 − Dividir la lista en subpartes más pequeñas. Cada uno debe tener intervalos iguales a h
Paso 4: ordene estas sublistas usando la ordenación por inserción
Paso 5: repita este paso 2 hasta que la lista esté ordenada.
Paso 6: imprima una lista ordenada.
Paso 7 – Detente.
Pseudocódigo:
PROCEDIMIENTO SHELL_SORT(ARRAY, N)
WHILE GAP < LENGTH(ARRAY) /3 :
GAP = ( INTERVALO * 3 ) + 1
END WHILE LOOP
WHILE GAP > 0 :
FOR (OUTER = GAP; OUTER < LENGTH(ARRAY); OUTER++):
INSERCIÓN_VALOR = MATRIZ[EXTERIOR]
INTERIOR = EXTERIOR;
WHILE INTERIOR > ESPACIO-1 Y ARRAY[INTERIOR – ESPACIO] >= VALOR_INSERCIÓN:
ARRAY[INTERIOR] = ARRAY[INTERIOR – ESPACIO]
INTERIOR = INTERIOR –
FIN DEL ESPACIO WHILE LOOP
ARRAY[INTER] = INSERCIÓN_VALOR
FIN DEL BUCLE
ESPACIO = (ESPACIO – 1) /3;
FIN MIENTRAS BUCLE
FIN SHELL_SORT
A continuación se muestra la implementación de ShellSort.
C++
// C++ implementation of Shell Sort
#include <iostream>
using namespace std;
/* function to sort arr using shellSort */
int shellSort(int arr[], int n)
{
// Start with a big gap, then reduce the gap
for (int gap = n/2; gap > 0; gap /= 2)
{
// Do a gapped insertion sort for this gap size.
// The first gap elements a[0..gap-1] are already in gapped order
// keep adding one more element until the entire array is
// gap sorted
for (int i = gap; i < n; i += 1)
{
// add a[i] to the elements that have been gap sorted
// save a[i] in temp and make a hole at position i
int temp = arr[i];
// shift earlier gap-sorted elements up until the correct
// location for a[i] is found
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
// put temp (the original a[i]) in its correct location
arr[j] = temp;
}
}
return 0;
}
void printArray(int arr[], int n)
{
for (int i=0; i<n; i++)
cout << arr[i] << " ";
}
int main()
{
int arr[] = {12, 34, 54, 2, 3}, i;
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Array before sorting: \n";
printArray(arr, n);
shellSort(arr, n);
cout << "\nArray after sorting: \n";
printArray(arr, n);
return 0;
}
Java
// Java implementation of ShellSort
class ShellSort
{
/* An utility function to print array of size n*/
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
/* function to sort arr using shellSort */
int sort(int arr[])
{
int n = arr.length;
// Start with a big gap, then reduce the gap
for (int gap = n/2; gap > 0; gap /= 2)
{
// Do a gapped insertion sort for this gap size.
// The first gap elements a[0..gap-1] are already
// in gapped order keep adding one more element
// until the entire array is gap sorted
for (int i = gap; i < n; i += 1)
{
// add a[i] to the elements that have been gap
// sorted save a[i] in temp and make a hole at
// position i
int temp = arr[i];
// shift earlier gap-sorted elements up until
// the correct location for a[i] is found
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
// put temp (the original a[i]) in its correct
// location
arr[j] = temp;
}
}
return 0;
}
// Driver method
public static void main(String args[])
{
int arr[] = {12, 34, 54, 2, 3};
System.out.println("Array before sorting");
printArray(arr);
ShellSort ob = new ShellSort();
ob.sort(arr);
System.out.println("Array after sorting");
printArray(arr);
}
}
/*This code is contributed by Rajat Mishra */
Python3
# Python3 program for implementation of Shell Sort
# Python3 program for implementation of Shell Sort
def shellSort(arr, n):
# code here
gap=n//2
while gap>0:
j=gap
# Check the array in from left to right
# Till the last possible index of j
while j<n:
i=j-gap # This will keep help in maintain gap value
while i>=0:
# If value on right side is already greater than left side value
# We don't do swap else we swap
if arr[i+gap]>arr[i]:
break
else:
arr[i+gap],arr[i]=arr[i],arr[i+gap]
i=i-gap # To check left side also
# If the element present is greater than current element
j+=1
gap=gap//2
# driver to check the code
arr2 = [12, 34, 54, 2, 3]
print("input array:",arr2)
shellSort(arr2,len(arr2))
print("sorted array",arr2)
# This code is contributed by Illion
C#
// C# implementation of ShellSort
using System;
class ShellSort
{
/* An utility function to
print array of size n*/
static void printArray(int []arr)
{
int n = arr.Length;
for (int i=0; i<n; ++i)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
/* function to sort arr using shellSort */
int sort(int []arr)
{
int n = arr.Length;
// Start with a big gap,
// then reduce the gap
for (int gap = n/2; gap > 0; gap /= 2)
{
// Do a gapped insertion sort for this gap size.
// The first gap elements a[0..gap-1] are already
// in gapped order keep adding one more element
// until the entire array is gap sorted
for (int i = gap; i < n; i += 1)
{
// add a[i] to the elements that have
// been gap sorted save a[i] in temp and
// make a hole at position i
int temp = arr[i];
// shift earlier gap-sorted elements up until
// the correct location for a[i] is found
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
// put temp (the original a[i])
// in its correct location
arr[j] = temp;
}
}
return 0;
}
// Driver method
public static void Main()
{
int []arr = {12, 34, 54, 2, 3};
Console.Write("Array before sorting :\n");
printArray(arr);
ShellSort ob = new ShellSort();
ob.sort(arr);
Console.Write("Array after sorting :\n");
printArray(arr);
}
}
// This code is contributed by nitin mittal.
Javascript
<script>
// Javascript implementation of ShellSort
/* An utility function to print array of size n*/
function printArray(arr)
{
let n = arr.length;
for (let i = 0; i < n; ++i)
document.write(arr[i] + " ");
document.write("<br>");
}
/* function to sort arr using shellSort */
function sort(arr)
{
let n = arr.length;
// Start with a big gap, then reduce the gap
for (let gap = Math.floor(n/2); gap > 0; gap = Math.floor(gap/2))
{
// Do a gapped insertion sort for this gap size.
// The first gap elements a[0..gap-1] are already
// in gapped order keep adding one more element
// until the entire array is gap sorted
for (let i = gap; i < n; i += 1)
{
// add a[i] to the elements that have been gap
// sorted save a[i] in temp and make a hole at
// position i
let temp = arr[i];
// shift earlier gap-sorted elements up until
// the correct location for a[i] is found
let j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
// put temp (the original a[i]) in its correct
// location
arr[j] = temp;
}
}
return arr;
}
// Driver method
let arr = [12, 34, 54, 2, 3];
document.write("Array before sorting<br>");
printArray(arr);
arr = sort(arr);
document.write("Array after sorting<br>");
printArray(arr);
// This code is contributed by unknown2108
</script>
Producción:
Array before sorting: 12 34 54 2 3 Array after sorting: 2 3 12 34 54
Complejidad de tiempo: la complejidad de tiempo de la implementación anterior de la ordenación de Shell es O(n 2 ). En la implementación anterior, la brecha se reduce a la mitad en cada iteración. Hay muchas otras formas de reducir las brechas que conducen a una mejor complejidad del tiempo. Vea esto para más detalles.
Complejidad
en el peor de los casos La complejidad en el peor de los casos para la clasificación de shell es O(n2
)
.
Entonces, la complejidad del mejor caso es Ω (n log (n))
Complejidad promedio del caso
La complejidad del caso promedio de clasificación shell depende del intervalo seleccionado por el programador.
θ(n log(n)2).
LA Complejidad Promedio de Casos: O(n*log n)
Complejidad de Espacio
La complejidad de espacio de la clasificación shell es O(1).
Aplicaciones de clasificación de conchas
1. Reemplazo de la ordenación por inserción, donde lleva mucho tiempo completar la tarea determinada.
2. Para llamar a la sobrecarga de la pila, usamos ordenación de shell.
3. cuando la recursión excede un límite particular, usamos shell sort.
4. Para conjuntos de datos de tamaño mediano a grande.
5. En clasificación por inserción para reducir el número de operaciones.
Referencias:
http://en.wikipedia.org/wiki/Shellsort
Instantáneas:

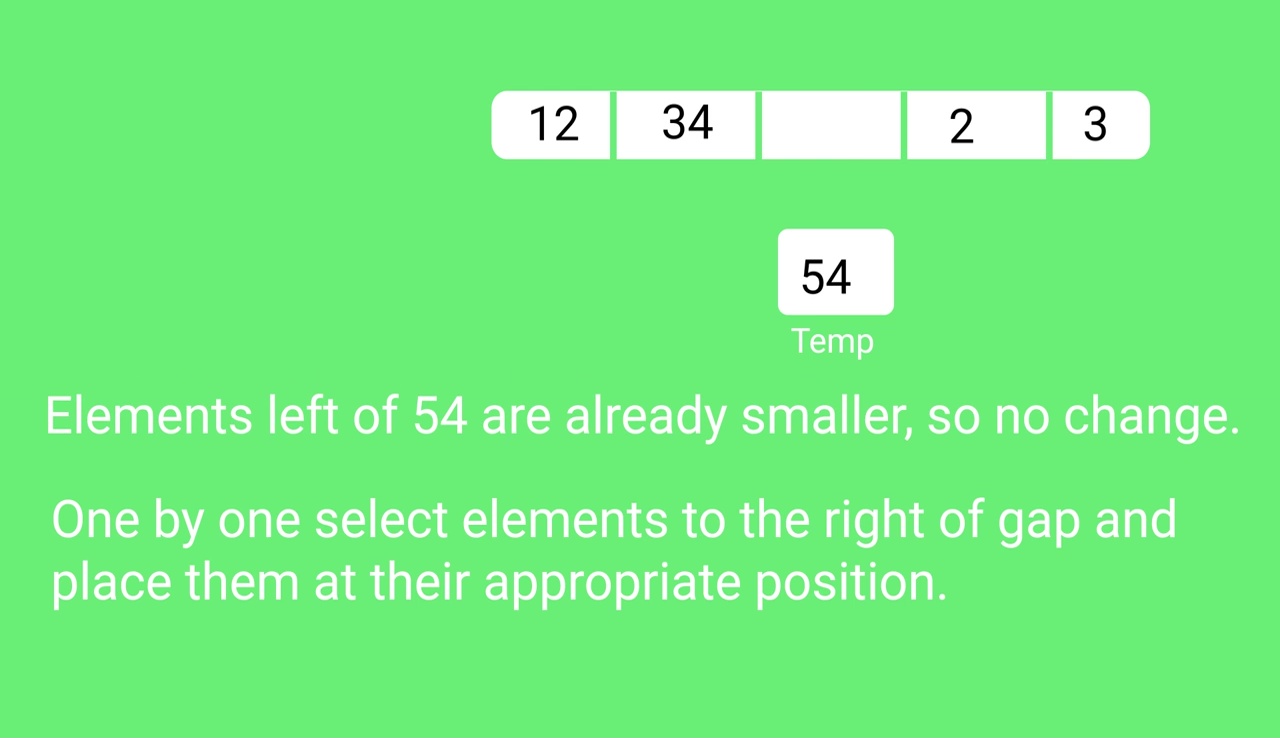




Cuestionario sobre clasificación de shell
Otros algoritmos de clasificación en GeeksforGeeks/GeeksQuiz:
- Clasificación de selección
- Ordenamiento de burbuja
- Tipo de inserción
- Ordenar por fusión
- Ordenar montón
- Ordenación rápida
- Clasificación Radix
- Clasificación de conteo
- Clasificación de cubo
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
