Dada una array, imprima el siguiente elemento más pequeño (NSE) para cada elemento. El NSE para un elemento x es el primer elemento más pequeño en el lado derecho de x en la array. Elementos para los que no existe un elemento más pequeño (en el lado derecho), considere NSE como -1.
Ejemplos:
a) Para cualquier array, el elemento más a la derecha siempre tiene NSE como -1.
b) Para una array ordenada en orden creciente, todos los elementos tienen NSE como -1.
c) Para la array de entrada [4, 8, 5, 2, 25} , el NSE para cada elemento es el siguiente.
Element NSE 4 --> 2 8 --> 5 5 --> 2 2 --> -1 25 --> -1
d) Para la array de entrada [13, 7, 6, 12}, los siguientes elementos más pequeños para cada elemento son los siguientes.
Element NSE 13 --> 7 7 --> 6 6 --> -1 12 --> -1
Método 1 (Simple)
Use dos bucles: El bucle exterior recoge todos los elementos uno por uno. El bucle interior busca el primer elemento más pequeño para el elemento elegido por el bucle exterior. Si se encuentra un elemento más pequeño, ese elemento se imprime como el siguiente; de lo contrario, se imprime -1.
Gracias a Sachin por proporcionar el siguiente código.
C++
// Simple C++ program to print
// next smaller elements in a given array
#include "bits/stdc++.h"
using namespace std;
/* prints element and NSE pair
for all elements of arr[] of size n */
void printNSE(int arr[], int n)
{
int next, i, j;
for (i = 0; i < n; i++)
{
next = -1;
for (j = i + 1; j < n; j++)
{
if (arr[i] > arr[j])
{
next = arr[j];
break;
}
}
cout << arr[i] << " -- "
<< next << endl;
}
}
// Driver Code
int main()
{
int arr[]= {11, 13, 21, 3};
int n = sizeof(arr) / sizeof(arr[0]);
printNSE(arr, n);
return 0;
}
// This code is contributed by shivanisinghss2110
C
// Simple C program to print next smaller elements
// in a given array
#include<stdio.h>
/* prints element and NSE pair for all elements of
arr[] of size n */
void printNSE(int arr[], int n)
{
int next, i, j;
for (i=0; i<n; i++)
{
next = -1;
for (j = i+1; j<n; j++)
{
if (arr[i] > arr[j])
{
next = arr[j];
break;
}
}
printf("%d -- %d\n", arr[i], next);
}
}
int main()
{
int arr[]= {11, 13, 21, 3};
int n = sizeof(arr)/sizeof(arr[0]);
printNSE(arr, n);
return 0;
}
Java
// Simple Java program to print next
// smaller elements in a given array
class Main {
/* prints element and NSE pair for
all elements of arr[] of size n */
static void printNSE(int arr[], int n)
{
int next, i, j;
for (i = 0; i < n; i++) {
next = -1;
for (j = i + 1; j < n; j++) {
if (arr[i] > arr[j]) {
next = arr[j];
break;
}
}
System.out.println(arr[i] + " -- " + next);
}
}
public static void main(String args[])
{
int arr[] = { 11, 13, 21, 3 };
int n = arr.length;
printNSE(arr, n);
}
}
Python
# Function to print element and NSE pair for all elements of list def printNSE(arr): for i in range(0, len(arr), 1): next = -1 for j in range(i + 1, len(arr), 1): if arr[i] > arr[j]: next = arr[j] break print(str(arr[i]) + " -- " + str(next)) # Driver program to test above function arr = [11, 13, 21, 3] printNSE(arr) # This code is contributed by Sunny Karira
C#
// Simple C# program to print next
// smaller elements in a given array
using System;
class GFG {
/* prints element and NSE pair for
all elements of arr[] of size n */
static void printNSE(int[] arr, int n)
{
int next, i, j;
for (i = 0; i < n; i++) {
next = -1;
for (j = i + 1; j < n; j++) {
if (arr[i] > arr[j]) {
next = arr[j];
break;
}
}
Console.WriteLine(arr[i] + " -- " + next);
}
}
// driver code
public static void Main()
{
int[] arr = { 11, 13, 21, 3 };
int n = arr.Length;
printNSE(arr, n);
}
}
// This code is contributed by Sam007
PHP
<?php
// Simple PHP program to print next
// smaller elements in a given array
/* prints element and NSE pair for
all elements of arr[] of size n */
function printNSE($arr, $n)
{
for ($i = 0; $i < $n; $i++)
{
$next = -1;
for ($j = $i + 1; $j < $n; $j++)
{
if ($arr[$i] > $arr[$j])
{
$next = $arr[$j];
break;
}
}
echo $arr[$i]." -- ". $next."\n";
}
}
// Driver Code
$arr= array(11, 13, 21, 3);
$n = count($arr);
printNSE($arr, $n);
// This code is contributed by Sam007
?>
Javascript
<script>
// Simple Javascript program to print
// next smaller elements in a given array
/* prints element and NSE pair
for all elements of arr[] of size n */
function printNSE(arr, n)
{
var next, i, j;
for (i = 0; i < n; i++)
{
next = -1;
for (j = i + 1; j < n; j++)
{
if (arr[i] > arr[j])
{
next = arr[j];
break;
}
}
document.write( arr[i] + " -- "
+ next+"<br>" );
}
}
// Driver Code
var arr= [11, 13, 21, 3];
var n = arr.length;
printNSE(arr, n);
</script>
11 -- 3 13 -- 3 21 -- 3 3 -- -1
Complejidad del tiempo : ![]()
El peor caso ocurre cuando todos los elementos se ordenan en orden decreciente.
Espacio Auxiliar: O(1)
Como se utiliza espacio adicional constante
Método 2 (usando el árbol de segmentos y la búsqueda binaria)
Este método también es bastante simple si uno conoce los árboles de segmentos y la búsqueda binaria. Consideremos una array ![]() y supongamos que NSE
y supongamos que NSE ![]() es
es ![]() , simplemente necesitamos realizar una búsqueda binaria
, simplemente necesitamos realizar una búsqueda binaria ![]() en el rango
en el rango ![]() de
de ![]() .
. ![]() será el primer índice
será el primer índice ![]() , tal que el rango mínimo de elementos desde el índice
, tal que el rango mínimo de elementos desde el índice ![]() hasta
hasta ![]() (
( ![]() ) es menor que
) es menor que ![]() .
.
C++
#include <bits/stdc++.h>
using namespace std;
// Program to find next smaller element for all elements in
// an array, using segment tree and binary search
// --------Segment Tree Starts Here-----------------
vector<int> seg_tree;
// combine function for combining two nodes of the tree, in
// this case we need to take min of two
int combine(int a, int b) { return min(a, b); }
// build function, builds seg_tree based on vector parameter
// arr
void build(vector<int>& arr, int node, int tl, int tr)
{
// if current range consists only of one element, then
// node should be this element
if (tl == tr) {
seg_tree[node] = arr[tl];
}
else {
// divide the build operations into two parts
int tm = (tr - tl) / 2 + tl;
build(arr, 2 * node, tl, tm);
build(arr, 2 * node + 1, tm + 1, tr);
// combine the results from two parts, and store it
// into current node
seg_tree[node] = combine(seg_tree[2 * node],
seg_tree[2 * node + 1]);
}
}
// query function, returns minimum in the range [l, r]
int query(int node, int tl, int tr, int l, int r)
{
// if range is invalid, then return infinity
if (l > r) {
return INT32_MAX;
}
// if range completely aligns with a segment tree node,
// then value of this node should be returned
if (l == tl && r == tr) {
return seg_tree[node];
}
// else divide the query into two parts
int tm = (tr - tl) / 2 + tl;
int q1 = query(2 * node, tl, tm, l, min(r, tm));
int q2 = query(2 * node + 1, tm + 1, tr, max(l, tm + 1),
r);
// and combine the results from the two parts and return
// it
return combine(q1, q2);
}
// --------Segment Tree Ends Here-----------------
void printNSE(vector<int> arr, int n)
{
seg_tree = vector<int>(4 * n);
// build segment tree initially
build(arr, 1, 0, n - 1);
int q, l, r, mid, ans;
for (int i = 0; i < n; i++) {
// binary search for ans in range [i + 1, n - 1],
// initially ans is -1 representing there is no NSE
// for this element
l = i + 1;
r = n - 1;
ans = -1;
while (l <= r) {
mid = (r - l) / 2 + l;
// q is the minimum element in range [l, mid]
q = query(1, 0, n - 1, l, mid);
// if the minimum element in range [l, mid] is
// less than arr[i], then mid can be answer, we
// mark it, and look for a better answer in left
// half. Else if q is greater than arr[i], mid
// can't be an answer, we should search in right
// half
if (q < arr[i]) {
ans = arr[mid];
r = mid - 1;
}
else {
l = mid + 1;
}
}
// print NSE for arr[i]
cout << arr[i] << " ---> " << ans << "\n";
}
}
// Driver program to test above functions
int main()
{
vector<int> arr = { 11, 13, 21, 3 };
printNSE(arr, 4);
return 0;
}
11 ---> 3 13 ---> 3 21 ---> 3 3 ---> -1
Complejidad del tiempo: ![]()
Para cada uno de ![]() los elementos de la array, hacemos una búsqueda binaria, que incluye
los elementos de la array, hacemos una búsqueda binaria, que incluye ![]() pasos, y cada paso cuesta
pasos, y cada paso cuesta ![]() operaciones [consultas mínimas de rango].
operaciones [consultas mínimas de rango].
Espacio Auxiliar: O(N)
Como espacio adicional se utiliza para almacenar los elementos del árbol de segmentos.
Método 3 (usando el árbol de segmentos y la compresión de coordenadas)
En este enfoque, construimos un árbol de segmentos sobre índices de elementos de array comprimidos:
- En algún lugar a lo largo de las líneas, construiríamos una array
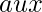 tal, que
tal, que ![Rendered by QuickLaTeX.com aux[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c51cc2b2f6d5d8a0f55e1cf17925ec96_l3.png) es el índice más pequeño en el que
es el índice más pequeño en el que 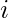 está presente en la array de entrada.
está presente en la array de entrada. - Es fácil ver que necesitamos comprimir la array de entrada para construir esta array
 porque si
porque si 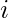 excede
excede 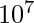 (el límite de memoria del juez en línea) es probable que obtengamos una falla de segmentación.
(el límite de memoria del juez en línea) es probable que obtengamos una falla de segmentación. - Para comprimir, ordenamos la array de entrada, y luego, para cada nuevo valor visto en la array, lo asignamos a un valor más pequeño correspondiente, si es posible. Utilice estos valores asignados para generar una
 array con el mismo orden que la array de entrada.
array con el mismo orden que la array de entrada. - Entonces, ahora que hemos terminado con la compresión, podemos comenzar con la parte de consulta:
- Supongamos que en el paso anterior comprimimos la array en
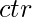 valores distintos. Establecido inicialmente
valores distintos. Establecido inicialmente ![Rendered by QuickLaTeX.com aux[i] = -1 \forall i \in [0, ctr)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1cc769c29e72d55332e95669d210d69_l3.png) , esto significa que no se procesa ningún valor en ningún índice a partir de ahora.
, esto significa que no se procesa ningún valor en ningún índice a partir de ahora. - Atraviese la array comprimida en orden inverso, esto implicaría que en el pasado solo habríamos procesado los elementos que están en el lado derecho.
- Para
![Rendered by QuickLaTeX.com compressed[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b0a6ffce17d80da18015cf91447dbd0_l3.png) , consulte (y almacene en
, consulte (y almacene en ![Rendered by QuickLaTeX.com ans[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f76da9bd7268ad5d90eb96f33f3ec30_l3.png) ) el índice de valores más pequeño
) el índice de valores más pequeño ![Rendered by QuickLaTeX.com [0, compressed[i])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18caccec3c52f7573a4c3ee48a42a5b5_l3.png) utilizando el árbol de segmentos, ¡este debe ser el NSE para
utilizando el árbol de segmentos, ¡este debe ser el NSE para ![Rendered by QuickLaTeX.com compressed[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b0a6ffce17d80da18015cf91447dbd0_l3.png) !
! - Actualizar el índice de
![Rendered by QuickLaTeX.com compressed[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b0a6ffce17d80da18015cf91447dbd0_l3.png) a
a 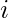 .
.
- Para
- Supongamos que en el paso anterior comprimimos la array en
- Almacenamos el índice de NSE para todos los elementos de la array, podemos imprimir fácilmente los NSE como se muestra en el código.
Nota: En la implementación, usamos INT32_MAX en lugar de -1 porque almacenar INT32_MAX no afecta nuestro árbol de segmento mínimo y aún sirve para identificar valores sin procesar.
Como espacio adicional se utiliza para almacenar los elementos del árbol de segmentos.
C++
#include <bits/stdc++.h>
using namespace std;
// Program to find next smaller element for all elements in
// an array, using segment tree and coordinate compression
// --------Segment Tree Starts Here-----------------
vector<int> seg_tree;
// combine function for combining two nodes of the tree, in
// this case we need to take min of two
int combine(int a, int b) { return min(a, b); }
// build function, builds seg_tree based on vector parameter
// arr
void build(vector<int>& arr, int node, int tl, int tr)
{
// if current range consists only of one element, then
// node should be this element
if (tl == tr) {
seg_tree[node] = arr[tl];
}
else {
// divide the build operations into two parts
int tm = (tr - tl) / 2 + tl;
build(arr, 2 * node, tl, tm);
build(arr, 2 * node + 1, tm + 1, tr);
// combine the results from two parts, and store it
// into current node
seg_tree[node] = combine(seg_tree[2 * node],
seg_tree[2 * node + 1]);
}
}
// update function, used to make a point update, update
// arr[pos] to new_val and make required changes to segtree
void update(int node, int tl, int tr, int pos, int new_val)
{
// if current range only contains one point, this must
// be arr[pos], update the corresponding node to new_val
if (tl == tr) {
seg_tree[node] = new_val;
}
else {
// else divide the range into two parts
int tm = (tr - tl) / 2 + tl;
// if pos lies in first half, update this half, else
// update second half
if (pos <= tm) {
update(2 * node, tl, tm, pos, new_val);
}
else {
update(2 * node + 1, tm + 1, tr, pos, new_val);
}
// combine results from both halfs
seg_tree[node] = combine(seg_tree[2 * node],
seg_tree[2 * node + 1]);
}
}
// query function, returns minimum in the range [l, r]
int query(int node, int tl, int tr, int l, int r)
{
// if range is invalid, then return infinity
if (l > r) {
return INT32_MAX;
}
// if range completely aligns with a segment tree node,
// then value of this node should be returned
if (l == tl && r == tr) {
return seg_tree[node];
}
// else divide the query into two parts
int tm = (tr - tl) / 2 + tl;
int q1 = query(2 * node, tl, tm, l, min(r, tm));
int q2 = query(2 * node + 1, tm + 1, tr, max(l, tm + 1),
r);
// and combine the results from the two parts and return
// it
return combine(q1, q2);
}
// --------Segment Tree Ends Here-----------------
void printNSE(vector<int> original, int n)
{
vector<int> sorted(n);
map<int, int> encode;
// -------Coordinate Compression Starts Here ------
// created a temporary sorted array out of original
for (int i = 0; i < n; i++) {
sorted[i] = original[i];
}
sort(sorted.begin(), sorted.end());
// encode each value to a new value in sorted array
int ctr = 0;
for (int i = 0; i < n; i++) {
if (encode.count(sorted[i]) == 0) {
encode[sorted[i]] = ctr++;
}
}
// use encode to compress original array
vector<int> compressed(n);
for (int i = 0; i < n; i++) {
compressed[i] = encode[original[i]];
}
// -------Coordinate Compression Ends Here ------
// Create an aux array of size ctr, and build a segtree
// based on this array
vector<int> aux(ctr, INT32_MAX);
seg_tree = vector<int>(4 * ctr);
build(aux, 1, 0, ctr - 1);
// For each compressed[i], query for index of NSE and
// update segment tree
vector<int> ans(n);
for (int i = n - 1; i >= 0; i--) {
ans[i] = query(1, 0, ctr - 1, 0, compressed[i] - 1);
update(1, 0, ctr - 1, compressed[i], i);
}
// Print -1 if NSE doesn't exist, otherwise print NSE
// itself
for (int i = 0; i < n; i++) {
cout << original[i] << " ---> ";
if (ans[i] == INT32_MAX) {
cout << -1;
}
else {
cout << original[ans[i]];
}
cout << "\n";
}
}
// Driver program to test above functions
int main()
{
vector<int> arr = { 11, 13, 21, 3 };
printNSE(arr, 4);
return 0;
}
11 ---> 3 13 ---> 3 21 ---> 3 3 ---> -1
Complejidad del tiempo : ![]()
Espacio Auxiliar: O(N)
Método 4 (usando la pila)
Este problema es similar al siguiente elemento mayor . Aquí mantenemos los elementos en orden creciente en la pila (en lugar de disminuir en el siguiente problema de elemento mayor).
- Empuje el primer elemento para apilar.
- Elija el resto de los elementos uno por uno y siga los siguientes pasos en bucle.
- Marca el elemento actual como siguiente .
- Si la pila no está vacía, compare a continuación con la parte superior de la pila. Si next es más pequeño que top, next es el NSE de top. Sigue saltando de la pila mientras top es mayor que next . el siguiente se convierte en el NSE para todos esos elementos reventados
- Empuje siguiente en la pila
- Después de que termine el bucle en el paso 2, extraiga todos los elementos de la pila e imprima -1 como el siguiente elemento para ellos.
Nota: Para lograr el mismo orden, usamos una pila de pares, donde el primer elemento es el valor y el segundo elemento es el índice del elemento de la array.
C++
// A Stack based C++ program to find next
// smaller element for all array elements
#include <bits/stdc++.h>
using namespace std;
// prints NSE for elements of array arr[] of size n
void printNSE(int arr[], int n)
{
stack<pair<int, int> > s;
vector<int> ans(n);
// iterate for rest of the elements
for (int i = 0; i < n; i++) {
int next = arr[i];
// if stack is empty then this element can't be NSE
// for any other element, so just push it to stack
// so that we can find NSE for it, and continue
if (s.empty()) {
s.push({ next, i });
continue;
}
// while stack is not empty and the top element is
// greater than next
// a) NSE for top is next, use top's index to
// maintain original order
// b) pop the top element from stack
while (!s.empty() && s.top().first > next) {
ans[s.top().second] = next;
s.pop();
}
// push next to stack so that we can find NSE for it
s.push({ next, i });
}
// After iterating over the loop, the remaining elements
// in stack do not have any NSE, so set -1 for them
while (!s.empty()) {
ans[s.top().second] = -1;
s.pop();
}
for (int i = 0; i < n; i++) {
cout << arr[i] << " ---> " << ans[i] << endl;
}
}
// Driver program to test above functions
int main()
{
int arr[] = { 11, 13, 21, 3 };
int n = sizeof(arr) / sizeof(arr[0]);
printNSE(arr, n);
return 0;
}
Java
// A Stack based Java program to find next
// smaller element for all array elements
// in same order as input.
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG {
/* prints element and NSE pair for all
elements of arr[] of size n */
public static void printNSE(int arr[], int n)
{
Stack<Integer> s = new Stack<Integer>();
HashMap<Integer, Integer> mp
= new HashMap<Integer, Integer>();
/* push the first element to stack */
s.push(arr[0]);
// iterate for rest of the elements
for (int i = 1; i < n; i++) {
if (s.empty()) {
s.push(arr[i]);
continue;
}
/* if stack is not empty, then
pop an element from stack.
If the popped element is greater
than next, then
a) print the pair
b) keep popping while elements are
greater and stack is not empty */
while (s.empty() == false
&& s.peek() > arr[i]) {
mp.put(s.peek(), arr[i]);
s.pop();
}
/* push next to stack so that we can find
next smaller for it */
s.push(arr[i]);
}
/* After iterating over the loop, the remaining
elements in stack do not have the next smaller
element, so print -1 for them */
while (s.empty() == false) {
mp.put(s.peek(), -1);
s.pop();
}
for (int i = 0; i < n; i++)
System.out.println(arr[i] + " ---> "
+ mp.get(arr[i]));
}
/* Driver program to test above functions */
public static void main(String[] args)
{
int arr[] = { 11, 13, 21, 3 };
int n = arr.length;
printNSE(arr, n);
}
}
Python3
# A Stack based Python3 program to find next
# smaller element for all array elements
# in same order as input.using System;
""" prints element and NSE pair for all
elements of arr[] of size n """
def printNSE(arr, n):
s = []
mp = {}
# push the first element to stack
s.append(arr[0])
# iterate for rest of the elements
for i in range(1, n):
if (len(s) == 0):
s.append(arr[i])
continue
""" if stack is not empty, then
pop an element from stack.
If the popped element is greater
than next, then
a) print the pair
b) keep popping while elements are
greater and stack is not empty """
while (len(s) != 0 and s[-1] > arr[i]):
mp[s[-1]] = arr[i]
s.pop()
""" push next to stack so that we can find
next smaller for it """
s.append(arr[i])
""" After iterating over the loop, the remaining
elements in stack do not have the next smaller
element, so print -1 for them """
while (len(s) != 0):
mp[s[-1]] = -1
s.pop()
for i in range(n):
print(arr[i], "--->", mp[arr[i]])
arr = [11, 13, 21, 3]
n = len(arr)
printNSE(arr, n)
# This code is contributed by decode2207.
C#
// A Stack based C# program to find next
// smaller element for all array elements
// in same order as input.using System;
using System;
using System.Collections.Generic;
class GFG {
/* prints element and NSE pair for all
elements of arr[] of size n */
public static void printNSE(int[] arr, int n)
{
Stack<int> s = new Stack<int>();
Dictionary<int, int> mp
= new Dictionary<int, int>();
/* push the first element to stack */
s.Push(arr[0]);
// iterate for rest of the elements
for (int i = 1; i < n; i++) {
if (s.Count == 0) {
s.Push(arr[i]);
continue;
}
/* if stack is not empty, then
pop an element from stack.
If the popped element is greater
than next, then
a) print the pair
b) keep popping while elements are
greater and stack is not empty */
while (s.Count != 0 && s.Peek() > arr[i]) {
mp.Add(s.Peek(), arr[i]);
s.Pop();
}
/* push next to stack so that we can find
next smaller for it */
s.Push(arr[i]);
}
/* After iterating over the loop, the remaining
elements in stack do not have the next smaller
element, so print -1 for them */
while (s.Count != 0) {
mp.Add(s.Peek(), -1);
s.Pop();
}
for (int i = 0; i < n; i++)
Console.WriteLine(arr[i] + " ---> "
+ mp[arr[i]]);
}
// Driver code
public static void Main()
{
int[] arr = { 11, 13, 21, 3 };
int n = arr.Length;
printNSE(arr, n);
}
}
// This code is contributed by
// 29AjayKumar
Javascript
<script>
// A Stack based Javascript program to find next
// smaller element for all array elements
// in same order as input.
/* prints element and NSE pair for all
elements of arr[] of size n */
function printNSE(arr, n)
{
let s = [];
let mp = new Map();
/* push the first element to stack */
s.push(arr[0]);
// iterate for rest of the elements
for (let i = 1; i < n; i++)
{
if (s.length==0)
{
s.push(arr[i]);
continue;
}
/* if stack is not empty, then
pop an element from stack.
If the popped element is greater
than next, then
a) print the pair
b) keep popping while elements are
greater and stack is not empty */
while (s.length != 0 && s[s.length - 1] > arr[i])
{
mp[s[s.length - 1]] = arr[i];
s.pop();
}
/* push next to stack so that we can find
next smaller for it */
s.push(arr[i]);
}
/* After iterating over the loop, the remaining
elements in stack do not have the next smaller
element, so print -1 for them */
while (s.length != 0)
{
mp[s[s.length - 1]] = -1;
s.pop();
}
for (let i = 0; i < n; i++)
document.write(arr[i] + " ---> " + mp[arr[i]] + "</br>");
}
let arr = [11, 13, 21, 3];
let n = arr.length;
printNSE(arr, n);
// This code is contributed by divyesh072019.
</script>
11 ---> 3 13 ---> 3 21 ---> 3 3 ---> -1
Complejidad del tiempo: ![]()
Como usamos solo un bucle for y todos los elementos en la pila se empujan y se abren al menos una vez.
Espacio Auxiliar: O(N)
Como espacio adicional se utiliza para almacenar los elementos de la pila.