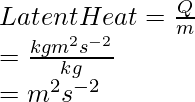Sistema de Unidades – Barcelona Geeks

La medición constituye el principio fundamental de varias otras ramas de la ciencia, es decir, los servicios de construcción e ingeniería. La medición se define como la acción de asociar valores numéricos con sus posibles magnitudes físicas y fenómenos. Las mediciones encuentran un papel en las actividades cotidianas en gran medida. Por lo tanto, es necesario estudiar y explorar los elementos asociados junto con sus fundamentos teóricos, condiciones y limitaciones. Define las unidades que se elegirán para la medición de diversos productos. También atiende a la comparación de unidades plausibles con las ya existentes de tipo similar.

La medición definió los nuevos estándares así como las transducciones de forma para las cantidades que no tienen ningún acceso posible para la comparación directa. Estas cantidades físicas se pueden convertir en señales de medición análogas.

Las mediciones pueden ser realizadas por los sentidos humanos sin ayuda, generalmente denominadas estimaciones. También se puede estimar mediante el uso de instrumentos, que pueden variar en complejidad desde reglas simples para medir longitudes hasta sistemas análogos altamente complejos para manejar y diseñar los productos más allá de las capacidades de los sentidos. Así, las medidas pueden ir desde la compra de cierta cantidad de leche (en L) hasta los mecanismos más complejos, como las ondas de radio de una estrella lejana o las radiaciones de una bomba nuclear. Por tanto, podemos considerar que una medida, implica siempre una transferencia de energía o interacción entre el objeto y el observador o instrumento observador.

Medida de la altura de una persona

Unidad

La unidad de una cantidad física específica se puede considerar como un estándar elegido arbitrariamente que se puede usar para estimar las cantidades que pertenecen a medidas similares. Las unidades son bien aceptadas y reconocidas por la gente y bien dentro de todos los lineamientos.

Una cantidad física se mide en términos de los estándares de medición elegidos.

El estándar elegido se reconoce como la unidad de esa cantidad física correspondiente. Una unidad estándar, en resumen, es una cantidad definida de una cantidad física. Estas unidades estándar se pueden reproducir rápidamente para crear una amplia variedad de unidades y son accesibles y aceptadas internacionalmente.

La medida de cualquier cantidad física se basa en una fórmula, nu,

donde, n = valor numérico de la medida de la cantidad,

u = unidad de la cantidad.

Estándar

La encarnación física real de la unidad de una cantidad física se denomina estándar de esa cantidad física. El estándar se expresa en términos del valor numérico (n) y la unidad (μ).

Medida de cantidad física = Valor numérico × Unidad

Por ejemplo: Longitud de una varilla = 12 m. Aquí 12 es su segmento numérico y m (metro) es la unidad.

Unidades Fundamentales

Las unidades fundamentales son de naturaleza elemental, es decir, pueden expresarse de forma independiente sin depender de ninguna otra cantidad física. Esto implica que no es posible resolverlo más en términos de cualquier otra cantidad física. También se denomina como una cantidad física básica. Las cantidades fundamentales tienen sus propios valores y unidades.

Magnitudes Fundamentales	Unidades Fundamentales	Símbolo
Longitud	metro	metro
Masa	kilogramo	kg
Tiempo	segundo	s
La temperatura	Kelvin	k
Corriente eléctrica	amperio	A
Intensidad luminosa	candela	discos compactos
Cantidad de sustancia	Topo	mol

Unidades Fundamentales Complementarias

Hay otras dos unidades fundamentales complementarias, a saber, el radián y el estereorradián son dos complementarios que miden el ángulo plano y el ángulo sólido respectivamente.

Cantidades fundamentales suplementarias	Unidad Complementaria
Ángulo plano	radián
Ángulo sólido	estereorradián

Radian (rad)
Un radian es equivalente a un ángulo subtendido en el centro de un círculo por un arco de longitud igual al radio del círculo. Es la unidad representada por el ángulo plano.

θ = 1 radián

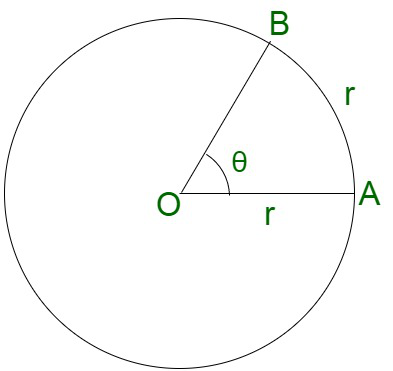
$dθ=\left(\frac{ds}{r}\right)\ radian$

Estereorradián (sr)
Un estereorradián es equivalente al ángulo sólido subtendido en el centro de una esfera por su superficie. Su área es equivalente al cuadrado del radio de la esfera. Es la unidad representada por el ángulo sólido. Ángulo sólido en estereorradián,

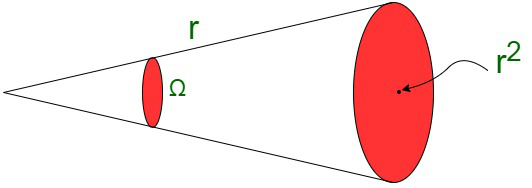
Ω = 1 estereorradián

$d&ohm; =\frac{Area\ cut\ out\ from\ the\ surface\ of\ sphere}{(Radius)^2}\\ d&ohm; =\left(\frac{dA}{r^2}\right)\ steradian$

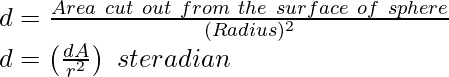
Propiedades de las Unidades Fundamentales

Cualquier unidad estándar debe tener las siguientes dos propiedades:

Invariabilidad
La unidad estándar debe ser invariable. Por lo tanto, definir la distancia entre la punta del dedo medio y el codo como unidad de longitud no es invariable.
Disponibilidad
La unidad estándar debe estar fácilmente disponible para compararla con otras cantidades.

Las siete unidades fundamentales del SI se han definido a continuación.

Metro (m)
Definido como 1650763,73 veces la longitud de onda, en el vacío de la luz naranja emitida en la transición de 2p ¹⁰ a 5d 5 .
Kilogramo (kg)
Definido como la masa de un cilindro de platino-iridio mantenido en Serves.
Segundo (s)
Tiempo tomado por 9192631770 ciclos de la radiación de la transición hiperfina en cesio – 133 cuando no es perturbada por campos externos.
Amperio (A)
La corriente constante que, si se mantiene en cada uno de dos alambres paralelos, rectos e infinitamente largos de sección transversal despreciable colocados a 1 m de distancia, en el vacío, produce entre los alambres una fuerza de 2 × 10 ^-7 newton por metro . longitud de los alambres.
Kelvin (K)
La temperatura se mide con el cero absoluto como cero y el punto triple del agua como punto fijo superior en la escala termodinámica. El intervalo se divide en 273,15 divisiones y cada división se considera unidad de temperatura.
Candela (cd)
La intensidad luminosa en la dirección perpendicular de una superficie de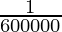 $\frac{1}{600000}$ metro cuadrado de un radiador lleno a la temperatura de congelación del platino bajo una presión de 101325 newtons por metro cuadrado.
Mol (mol)
El mol es la cantidad de cualquier sustancia que contiene tantas entidades elementales como átomos hay en 0,012 kg del isótopo de carbono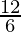 $\frac{12}{6}$ C.

Unidades derivadas

Las unidades derivadas están en uso para los productos básicos donde las unidades se obtienen de una combinación de unidades fundamentales. A las unidades derivadas a veces se les asignan nombres. Por ejemplo, la unidad SI de fuerza es kg ms ^-2 , denominada Newton (N). La unidad de potencia es kg m ² s ^-3 , denominada vatio (W).

Pasos para encontrar Unidades Derivadas

Obtener la fórmula para la cantidad cuya unidad se va a derivar.
Unidades de sustitución de todas las cantidades involucradas. Las unidades elegidas deben pertenecer todas a un sistema de unidades en su forma fundamental o estándar.
Simplifique para la unidad derivada de la cantidad para calcular su unidad final.

Ejemplo : Calcular la unidad de velocidad.

Ya que sabemos que la velocidad es una cantidad derivada, obtenida a partir de la distancia y el tiempo (cantidades fundamentales).

matemáticamente,

velocidad = desplazamiento/tiempo

Unidad SI de velocidad = $\frac{S.I.\ unit\ of\ displacement}{ S.I.\ unit\ of\ time}$ = m/s

Por lo tanto, la unidad SI de velocidad es m/s.

Algunas unidades derivadas importantes

Algunas de las unidades derivadas han recibido nombres específicos, según el aumento de su uso, aunque no se reconocen en las unidades SI.

Micras (mm) = 10 ^-6 m
Angstrom (Å) = 10 ^-10 m
Fermi (fm) = 10 ^-15 m
Granero (b) = 10 ^-28 m ²

Sistemas de Unidades

Cualquier sistema de unidades contiene el conjunto completo de unidades tanto fundamentales como derivadas, para todo tipo de cantidades físicas. El sistema preferido de unidades es el siguiente:

Sistema CGS (Centímetro Gramo Segundo)
La unidad de longitud es el centímetro, la unidad de masa es el gramo y la unidad de tiempo es el segundo de acuerdo con las pautas de este sistema.
Sistema FPS (Foot Pound Second)
La unidad de longitud es el pie, la unidad de masa es la libra y la unidad de tiempo es el segundo de acuerdo con las pautas de este sistema.
Sistema MKS (Metro Kilogramo Segundo)
La unidad de longitud es el metro, la unidad de masa es el kilogramo y la unidad de tiempo es el segundo de acuerdo con las pautas de este sistema.
Sistema SI
El Sistema Internacional de Unidades, es decir, el sistema SI, contiene siete unidades fundamentales y dos unidades fundamentales suplementarias.

Nota:

Durante el cálculo de valores para cualquier cantidad física, las unidades para las cantidades derivadas involucradas se tratan como cantidades algebraicas hasta que se obtienen las unidades deseadas.

Ventajas del sistema de unidades SI

Se prefiere la unidad de medida SI a otras unidades de medida porque,

Es aceptado internacionalmente.
Es un sistema métrico.
Es un sistema de unidades racional y coherente,
Fácil conversión entre los sistemas de unidades CGS y MKS.
Utiliza el sistema decimal, que es fácil de entender y aplicar.

Otras unidades importantes de longitud

Las distancias pueden ser infinitamente mayores en magnitud, lo que no se puede representar en términos de metros o kilómetros. Por ejemplo, las distancias de los planetas y las estrellas, etc. Por lo tanto, es necesario utilizar algunas unidades de longitud más grandes, como ‘unidad astronómica’, ‘año luz’, parsec’, etc. al realizar dichos cálculos, algunos de los cuales son:

Unidad astronómica: la separación promedio entre la Tierra y el sol.
1 UA = 1.496 x 10 ¹¹ m.
Año luz: la distancia recorrida por la luz en el vacío en un año.
1 año luz = 9,46 x 10 ¹⁵ m.
Parsec: la distancia a la que un arco de longitud de una unidad astronómica subtiende un ángulo de un segundo en un punto.
1 parsec = 3,08 x 10 ¹⁶ m
Fermi: el tamaño de un núcleo se expresa en ‘fermi’.
1 fermi = Si = 10 ^-15 m
Angstrom – Tamaño de un átomo diminuto
1 angstrom = 1A = 10 ^-10 m

Problemas de muestra

Problema 1. Convertir la unidad de G, que es constante gravitatoria, G = 6,67 x 10 ^-11 Nm ² /kg ² en sistema CGS.

Solución:

Desde que tenemos

G = 6,67 x 10- ¹¹ Nm ² /kg ²

Convirtiendo kg en gramos, 1 kg = 1000 gms

= 6,67 x 10- ¹¹ x 10 ⁸ x 10 ³ cm ³ /g ¹ s ²

= 6,67 x 10 ⁸ cm3/g1 s2

Problema 2. Nombre las unidades SI de las siguientes mercancías:

una. Presión

b. Ángulo sólido

C. Intensidad luminosa.

Solución:

una. Pascal

b. estereorradián

C. Candela

Problema 3. Derive la unidad SI de calor latente.

Solución:

Calor latente = $\frac{Heat energy}{Mass}$

$Latent\space Heat = \frac{Q}{m} \\ =\frac{ kg m^2 s^{-2}}{kg} \\ = m^2 s^{-2}$

Problema 4: ¿Cómo se relacionan A ⁰ y AU?

Solución:

Describiendo ambas cantidades en términos de metros,

A ^o = 10 ^-10 m

y 1 UA = 1,49610 ¹¹ m.

Por lo tanto,

1 AU = 1.496 x 10 ¹¹ x 10 ¹⁰ A ⁰

1 AU = 1.496 x 10 ²¹ A ⁰

Problema 5: Describe 1 año luz en metros.

Solución:

Un año luz es la distancia recorrida por la luz en 1 año con la velocidad de la luz:

= 9,46 x 10 ¹¹ m

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Problemas de muestra

Deja una respuesta Cancelar la respuesta