Sistemas de gestión de bases de datos | conjunto 6

Se han hecho las siguientes preguntas en el examen GATE 2009 CS. 

1) Considere dos transacciones T1 y T2, y cuatro calendarios S1, S2, S3, S4 de T1 y T2 como se indica a continuación: 
T1 = R1[X] W1[X] W1[Y] 
T2 = R2[X] R2[Y ] W2[Y] 
S1 = R1[X] R2[X] R2[Y] W1[X] W1[Y] W2[Y] 
S2 = R1[X] R2[X] R2[Y] W1[X] W2 [Y] W1[Y] 
S3 = R1[X] W1[X] R2[X] W1[Y] R2[Y] W2[Y] 
S1 = R1[X] R2[Y]R2[X]W1[X ] W1[Y] W2[Y] 
¿Cuáles de los programas anteriores son serializables en conflicto?  
(A) S1 y S2 
(B) S2 y S3 
(C) Solo S3 
(D) Solo S4 

Respuesta (B) 
Puede haber dos horarios de serie posibles T1 T2 y T2 T1. El horario serial T1 T2 tiene la siguiente secuencia de operaciones 
R1[X] W1[X] W1[Y] R2[X] R2[Y] W2[Y] 
Y el horario T2 T1 tiene la siguiente secuencia de operaciones. 
R2[X] R2[Y] W2[Y] R1[X] W1[X] W1[Y] 
El programa S2 es equivalente en conflicto a T2 T1 y S3 es equivalente en conflicto a T1 T2. 

2) Sean R y S esquemas relacionales tales que R={a,b,c} y S={c}. Ahora considere 
las siguientes consultas en la base de datos: 
 

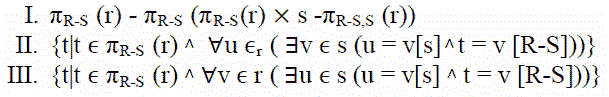
IV) SELECT R.a, R.b
       FROM R,S
            WHERE R.c=S.c

¿Cuáles de las consultas anteriores son equivalentes?  
(A) I y II 
(B) I y III 
(C) II y IV 
(D) III y IV 

La respuesta (A) 
I y II describen el operador de división en Álgebra relacional y Cálculo relacional de tuplas, respectivamente. Consulte la página 3 de este y las diapositivas 9 y 10 de este para obtener más detalles. 

3) Considere el siguiente esquema relacional: 

Suppliers(sid:integer, sname:string, city:string, street:string)
Parts(pid:integer, pname:string, color:string)
Catalog(sid:integer, pid:integer, cost:real)

Considere la siguiente consulta relacional en la base de datos anterior: 
 

SELECT S.sname
    FROM Suppliers S
        WHERE S.sid NOT IN (SELECT C.sid
                            FROM Catalog C
                            WHERE C.pid NOT IN (SELECT P.pid  
                                                FROM Parts P                                                                                                    
                                                WHERE P.color<> 'blue'))

Suponga que las relaciones correspondientes al esquema anterior no están vacías. ¿Cuál de las siguientes es la interpretación correcta de la consulta anterior? 

(A) Busque los nombres de todos los proveedores que hayan suministrado una pieza que no sea azul. 
(B) Encuentre los nombres de todos los proveedores que no hayan suministrado una pieza que no sea azul. 
(C) Encuentre los nombres de todos los proveedores que han suministrado solo piezas azules. 
(D) Encuentre los nombres de todos los proveedores que no han suministrado solo piezas azules. 

Respuesta (A) 
La subconsulta “ SELECT P.pid FROM Parts P WHERE P.color<> ‘blue’ ” da pids de partes que no son azules. La subconsulta más grande “ SELECCIONE C.sid DEL Catálogo C DONDE C.pid NO ESTÁ EN (SELECCIONE P.pid DE Partes P DONDE P.color<> ‘azul’) ” brinda los sid de todos aquellos proveedores que han suministrado partes azules. La consulta completa proporciona los nombres de todos los proveedores que han suministrado una pieza no azul. 

4) Suponga que, en la relación de proveedores anterior, cada proveedor y cada calle dentro de una ciudad tiene un nombre único y (nombre, ciudad) forma una clave candidata. No se implican otras dependencias funcionales distintas de las implícitas en las claves principal y candidata. ¿Cuál de las siguientes es VERDADERA sobre el esquema anterior?  
(A) El esquema está en FNBC 
(B) El esquema está en 3FN pero no en FNBC 
(C) El esquema está en 2FN pero no en 3FN 
(D) El esquema no está en 2FN 

Respuesta (A) 
Una relación está en BCNF si para cada una de sus dependencias X ? Y, se cumple al menos una de las siguientes condiciones: 

    X ? Y is a trivial functional dependency (Y ? X)
    X is a superkey for schema R 

Dado que (nombre, ciudad) forma una clave candidata, no existe una dependencia no trivial X ? Y donde X no es una superclave 

Consulte GATE Corner para ver todos los documentos/soluciones/explicaciones del año anterior, programa de estudios, fechas importantes, notas, etc. 

Escriba comentarios si encuentra que alguna de las respuestas/explicaciones es incorrecta, o si desea compartir más información sobre los temas discutidos anteriormente.