ordenar() frente a orden_parcial() frente a nth_element() + ordenar() en C++ STL

En este artículo, discutiremos la diferencia entre sort() , shared_sort( ) y nth_element() +sort().

A continuación se muestra la ilustración de las funciones anteriores:

1. sort(): C++ STL proporciona una función sort() que ordena una lista de elementos en tiempo O(N*log N). De forma predeterminada, sort() ordena una array en orden ascendente. A continuación se muestra el programa para ilustrar sort():

   // C++ program to illustrate the default behaviour // of sort() in STL #include <bits/stdc++.h> using namespace std;    // Driver Code int main() {     // Given array of elements     int arr[] = { 1, 5, 8, 9, 6, 7, 3, 4, 2, 0 };     int n = sizeof(arr) / sizeof(arr[0]);        // Function sort() to sort the element of     // the array in increasing order     sort(arr, arr + n);        // Print the array elements after sorting     cout << "\nArray after sorting using "             "default sort is: \n";     for (int i = 0; i < n; ++i) {         cout << arr[i] << " ";     }        return 0; }

   Producción:

   Array after sorting using default sort is : 
   0 1 2 3 4 5 6 7 8 9
   

2. shared_sort(): una de las variantes de std::sort() es std::partial_sort() , que se usa para ordenar no todo el rango, sino solo una parte parcial del mismo. Reorganiza los elementos en el rango [first, last) , de tal manera que los elementos antes del medio se ordenan en orden ascendente, mientras que los elementos después del medio se dejan sin ningún orden específico.
   A continuación se muestra el programa para ilustrar shared_sort():

   // C++ program to demonstrate the use of // partial_sort() #include <bits/stdc++.h> using namespace std;    // Driver Code int main() {     // Given array of elements     vector<int> v = { 1, 3, 1, 10, 3, 3, 7, 7, 8 };        // Using std::partial_sort() to sort     // first 3 elements     partial_sort(v.begin(), v.begin() + 3, v.end());        // Displaying the vector after applying     // partial_sort()     for (int ip : v) {         cout << ip << " ";     }        return 0; }

   Producción:

   1 1 3 10 3 3 7 7 8
   

   La complejidad de sort_parcial() es O(N*log K) donde N es el número de elementos en el arreglo y K es el número de elementos entre el medio y el inicio. La ordenación_parcial () es más rápida que la ordenación() si K es significativamente menor que N , ya que la ordenación_parcial () ordenará los primeros K elementos, mientras que la ordenación() ordenará todos los N elementos. El tiempo de ejecución O(N*log K)
   en el peor de los casos de part_sort() no cuenta toda la historia. Su tiempo de ejecución de caso promedio en la entrada aleatoria es O(N + K*log K + K*(log K)*(log Nk)) .
   Debido a que se hace muy poco trabajo para ignorar cada elemento que no se encuentra entre los K más pequeños vistos hasta ahora en una sola comparación, el factor constante resulta ser difícil de superar para K pequeño , incluso con un algoritmo asintóticamente mejor.

3. nth_element(): El nth_element() es un algoritmo STL que reorganiza la lista de tal manera que el elemento en la n-ésima posición es el que debería estar en esa posición si ordenamos la lista.
   No ordena la lista, solo que todos los elementos que preceden al n-ésimo elemento no son mayores que él, y todos los elementos que lo siguen no son menores que él.
   A continuación se muestra el programa para ilustrar nth_element():

   // C++ program to demonstrate the use // of std::nth_element #include <bits/stdc++.h> using namespace std;    // Driver Code int main() {     // Given array v[]     int v[] = { 3, 2, 10, 45, 33, 56, 23, 47 };        // Using nth_element with n as 5     nth_element(v, v + 4, v + 8);        // Since, n is 5 so 5th element     // should be sorted     for (int i = 0; i < 8; i++)         cout << v[i] << " ";        return 0; }

   Producción:

   3 2 10 23 33 56 45 47
   

A continuación se muestra la comparación de referencia entre tres algoritmos, variando N de 0 a 10 ⁷ (eje X en el gráfico):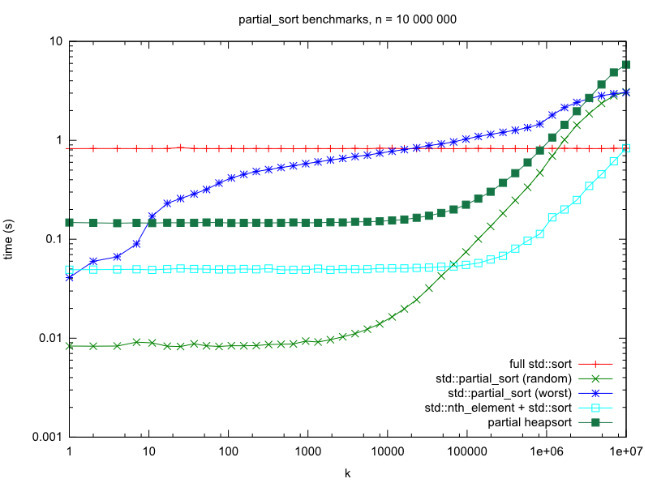

La solución nth_element() + sort() es asintóticamente más rápida y ofrece mejores resultados para K más grandes (que es la mayoría de ellos, tenga en cuenta la escala logarítmica). Pero pierde ante shared_sort() en una entrada aleatoria para K < 70000 , hasta por un factor de 6 .